По дисциплине
“Теория вероятностей
и
математическая статистика”
Новосибирск
Аннотация
Настоящее учебное пособие предназначено для практического освоения дисциплины “Теория вероятностей и математическая статистика”, активизации работы студентов на практических занятиях и помощи при самостоятельной работе. Оно ориентировано на формирование и закрепление знаний, умений и навыков по данной дисциплине.
Для студентов экономических вузов и факультетов.
ПРЕДИСЛОВИЕ
Настоящая рабочая тетрадь является учебным пособием, предназначенным для изучения дисциплины “Теория вероятностей и математическая статистика” как на практических занятиях, так и самостоятельно. Она составлена в соответствии с требованиями учебной программы данной дисциплины и требованиями Государственного образовательного стандарта.
Рабочая тетрадь предназначена для практического освоения дисциплины “Теория вероятностей и математическая статистика”. Ее использование направлено на активизацию работы студентов, ориентировано на формирование и закрепление знаний, умений и навыков по данной дисциплине.
Материал, изложенный в пособии, охватывает традиционные разделы дисциплины “Теория вероятностей и математическая статистика”, предусмотренные учебной программой по высшей математике для студентов вузов, обучающихся по экономическим специальностям:
· основные понятия теории вероятностей;
· схема Бернулли и предельные теоремы в схеме Бернулли;
· случайные величины и их характеристики;
· элементы математической статистики.
В начале каждой темы приводятся основные понятия, теоретические положения и формулы, которые непосредственно используются при решении задач данной темы. Даются подробные решения типовых задач. Некоторые задачи решаются разными способами, что, несомненно, способствует развитию творческих способностей студентов, учит их искать разные варианты и выбирать оптимальные решения.
В каждой теме приведены примеры и задачи различной трудности, которые расположены в порядке возрастания их сложности. Поэтому пособие может быть использовано лицами с различным уровнем математической подготовки. Объяснения решений приведены в доступной для студентов форме, что поможет овладеть навыками самостоятельного решения задач по теории вероятностей и математической статистике.
Значок g в конце решения примера означает, что он решен полностью, а его отсутствие указывает на необходимость решения каких-то частей примера.
РАЗДЕЛ 1. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ
Тема 1. Пространство элементарных исходов и события.
Операции над событиями и отношения между ними
| Название | Обозначение | Определение |
| Испытание (опыт, эксперимент) | Выполнение некоторого комплекса условий | |
| Элементарный исход (элементарное событие) | w | Простейший неразложимый результат испытания |
| Пространство элементарных исходов (элементарных событий) | W | Множество всех возможных элементарных исходов испытания |
| Событие | A, B, C, … | Любой результат (исход) испытания |
| Событие A происходит (осуществляется) | В результате испытания происходит (осуществляется) какой-либо элементарный исход wÎ A | |
| Достоверное событие | W | Событие, которое в результате испытания обязательно происходит |
| Невозможное событие | Æ | Событие, которое в результате испытания произойти не может |
| Случайное событие | A, B, C, … | Событие, которое в результате испытания как может произойти, так и не произойти |
| Сумма (объединение) событий А и В | А + В (A È В) | Событие, которое заключается в появлении хотя бы одного из них, т.е. в появлении либо только события А, либо только события В, либо этих событий вместе |
| Сумма (объединение) событий А 1, А 2,..., Аn | А 1 + А 2 +... + Аn =
 (А 1 È А 2 È... È Аn
(А 1 È А 2 È... È Аn  ) )
| Событие, которое заключается в появлении хотя бы одного из этих n событий |
| Произведение (пересечение) событий А и В | А × В (A Ç В) | Событие, которое состоит в появлении этих событий вместе |
| Произведение (пересечение) событий А 1, А 2,..., Аn | А 1 · А 2 ·... · Аn =  (А 1 Ç А 2 Ç... Ç Аn
(А 1 Ç А 2 Ç... Ç Аn  ) )
| Событие, которое состоит в совместном появлении всех этих n событий |
| Событие дополнительное (противоположное) к событию А | 
| Событие, заключающееся в непоявлении события А |
| Разность событий А и В | A \ B
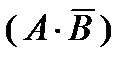
| Событие, которое заключается в появлении события A и непоявлении события B |
| Событие А влечет за собойсобытие В (событие А включаетсявсобытие В) | A Ì B | Из наступления события A следует наступление события B |
| Равенство (эквивалентность) событий А и В | А = В | А Ì В и В Ì А (появление одного из этих событий влечет за собой появление другого) |
| Несовместность событий А и В | AB = Æ | Совместное появление событий А и В невозможно |
| Попарная несовместность событий А 1, А 2,..., Аn | Ai × Aj = Æ, i, j = 1, 2, …, n; i ¹ j | Любые два события из этой совокупности вместе произойти не могут |
| Полная группа событий А 1, А 2,..., Аn | 
| В результате испытания обязательно произойдет хотя бы одно из этих n событий |
На рис. 1.1 изображены основные соотношения между событиями А и В. Результаты операций изображены в виде затемненных фигур.

Рис 1.1. а) Сумма (объединение) событий А + В (А È B);
b) произведение событий А × В; с) разность событий А \ В;
d) противоположное событие 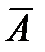 ; e) отношение включения А Ì В; f) отношение несовместности А × В = Æ.
; e) отношение включения А Ì В; f) отношение несовместности А × В = Æ.


Рис. 1.2. Полная группа событий. Рис. 1.3. Полная группа попарно
несовместных событий.
Операции сложения и умножения событий обладают следующими свойствами:
· A + B = B + A, AB = BA (коммутативность);
· (A + B) + C = A + (B + C), A (BC) = (AB) C (ассоциативность);
· (A + B) C = AC + BC (дистрибутивность);
·  (двойственность).
(двойственность).
Если А – конечное множество, т.е. множество, состоящее из конечного числа элементов, то будем обозначать через N (A) число элементов в А и N º N (W).
Пример 1.1. Пусть испытание состоит в том, что монета подбрасывается один раз.
Выбрать соответствующее множество W в качестве пространства элементарных исходов1) этого испытания.
Решение. Будем здесь и в дальнейшем буквой Г обозначать исход, состоящий в выпадении монеты гербом вверх, буквой Р – решкой (цифрой) вверх. Кроме того, монета, возможно, встанет на ребро, укатится куда-нибудь и т.д., но такие исходы мы будем исключать из рассмотрения. Тогда в качестве пространства элементарных исходов можем выбрать множество, состоящее из этих двух элементов:
W = {w1, w2}, где w1 = { Г }, w2 = { Р }. g
Пример 1.2. Монета подбрасывается дважды или, что эквивалентно, две монеты подбрасываются одновременно один раз. В предположениях примера 1.1 выбрать соответствующее множество в качестве пространства элементарных исходов данного испытания и с помощью его элементов описать следующие события:
A = {выпадет один герб}; B = {выпадет хотя бы один герб};
C = {выпадет не более двух гербов}; D = {выпадет три герба}.
Вычислить N (W), N (A), …, N (D).
Решение. Испытание – подбрасывание монеты дважды (или двух монет одновременно). В предположениях и обозначениях решения примера 1.1 в качестве пространства элементарных исходов данного испытания можно выбрать множество
W = {w1, w2, w3, w4} = { ГГ, ГР, РГ, РР }.
Здесь исход ГР, например, означает, что при первом бросании появится герб, а при втором – решка.
События A, B и C опишутся следующим образом:
A = {w2, w3} = { ГР, РГ }; B = {w1, w2, w3} = { ГГ, ГР, РГ };
C = {выпадет не более двух гербов} = {w1, w2, w3, w4} = W – достоверное событие.
Событие D = {выпадет три герба} = Æ – невозможное событие.
Непосредственно находим, что N (W) = 4; N (A) = 2; N (B) =3; N (C) = 4; N (D) = 0. g
Пример 1.3. Монета подбрасывается три раза. Описать пространство элементарных исходов W данного испытания и с помощью его элементов описать следующие события:
A = {выпадет один герб}; B = {выпадут два герба}; C = {выпадет не менее двух гербов};
D = {выпадет не более двух гербов}; E = {выпадет хотя бы один герб}.
Вычислить N, N (A), …, N (E).
Решение. Испытание – подбрасывание монеты три раза. В качестве пространства элементарных исходов данного испытания выбираем множество
W = {w1, w2, …, w8} = { ГГГ, ГГР, ГРГ, РГГ, ГРР, РГР, РРГ, РРР }.
Здесь исход ГГР, например, означает, что при первых двух подбрасываниях появятся гербы, а при третьем – решка. Очевидно, N = N (W) = 8.
Событие A = {выпадет один герб} = { ГРР, РГР, РРГ }, N (A) = 3;
событие B = {выпадут два герба} = { …….., …….., …….. }, N (В) = …...;
событие C = {выпадет не менее двух гербов} = { }, N (C) =;
событие D = {выпадет не более двух гербов} = { }, N (D) =;
событие E = {выпадет хотя бы один герб} = { }, N (E) =.
Пример 1.4. Монета подбрасывается пять раз. Описать пространство элементарных исходов W данного испытания и события A, B, …, E примера 1.3.
Вычислить N, N (A), …, N (E).
Пример 1.5. Подбрасывается игральная кость, которая представляет собой правильный куб, на гранях которого нанесены точки от одной до шести. Если при этом на верхней грани оказывается, например, одна точка, то говорят, что выпало одно очко; если две точки, то два очка и т.д. Описать пространство элементарных исходов и следующие события:
A = {выпадет четное число очков}; B = {выпадет нечетное число очков};
C = {выпадет число очков, кратное трем}; D = {выпадет хотя бы одно очко};
E = {выпадет 8 очков}.
Вычислить N, N (A), …, N (E).
Решение. Испытание – подбрасывание игральной кости, элементарный исход которого есть грань куба с определенным числом точек. Поскольку нас интересует только число точек на грани (число очков), то каждый элементарный исход w i испытания можно отождествить с числом выпавших очков i. Тогда W = {w i, i = 1, 2, …, 6} = {1, 2, 3, 4, 5, 6} и N = N (W) = 6.
Событие A = {2, 4, 6}, N (A) = 3; событие B = {1, 3, 5}, N (B) = 3;
событие C = {3, 6}, N (C) = 2; событие D = W – достоверное событие, N (D) = 6.
Событие E = {выпадет 8 очков} = Æ – невозможное событие, N (E) = 0. g
Пример 1.6. Игральная кость подбрасывается два раза или, что эквивалентно, две игральные кости подбрасываются одновременно один раз. Описать пространства элементарных исходов данного испытания и следующие события:
A = {сумма выпавших очков будет равна 8};
B = {произведение выпавших очков будет равно 8};
C = {оба раза выпадет четное число очков};
D = {сумма выпавших очков будет не более 12};
E = {произведение выпавших очков будет равно 7}.
Вычислить N, N (A), …, N (E).
Решение. Испытание – игральная кость подбрасывается два раза (или подбрасываются две игральные кости). В соответствии с решением примера 1.5 каждый элементарный исход данного испытания можно описать парой чисел (i, j), где i – число очков, выпавших при первом подбрасывании игральной кости (на первой кости), j – при втором подбрасывании (на второй кости). Тогда пространства элементарных исходов есть множество

Нетрудно подсчитать, что N = N (W) = 6´6 = 36.
Событие A = {(2, 6); (3, 5); (4, 4); (5, 3); (6, 2)}, N (A) = 5;
событие B = {(2, 4); (4, 2)}, N (B) = 2;
событие C = 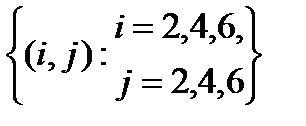 , N (C) = 3´3 = 9;
, N (C) = 3´3 = 9;
событие D = W – достоверное событие, N (D) = N (W) = 36;
событие E = Æ – невозможное событие, N (E) = N (Æ) = 0. g
Пример 1.7. Игральная кость подбрасывается три раза. Описать пространства элементарных исходов данного испытания и следующие события:
A = {сумма выпавших очков будет равна 4}; B = {на всех костях будет четное число очков};
C = {четное число очков будет на первой кости};
D = {четное число очков будет только на первой кости};
E = {произведение выпавших очков будет четно}; F = {сумма выпавших очков будет четна}.
Вычислить N, N (A), …, N (F).
Решение. Испытание –
Элементарный исход испытания w =, где
Пространства элементарных исходов W =
Событие A = N (A) =;
событие B = N (B) =;
событие C = N (C) =;
событие D = N (D) =;
событие E = N (E) =;
событие F = N (F) =.
Пример 1.8. Имеется 30 экзаменационных билетов, среди которых первые 10 билетов «счастливые», а остальные – «несчастливые». Два студента из группы поочередно и без возвращения берут по одному билету. Описать пространство элементарных исходов данного испытания и следующие события, состоящие в том, что:
а) студенты возьмут «счастливые» билеты;
b) первый студент возьмет «счастливый» билет;
c) только первый студент возьмет «счастливый» билет;
d) первый студент возьмет первый билет, а второй – «несчастливый»;
e) первый студент возьмет первый билет, а второй – последний.
Решение. Испытание – два студента поочередно и без возвращения берут по одному билету из 30 экзаменационных билетов. Интересующие нас события, описанные в п.п. a) – e), обозначим через A, B, …, E соответственно. Каждый элементарный исход рассматриваемого испытания есть пара билетов у студентов. Дальнейшее решение возможно двумя способами, один из которых неверен.
1-й способ. Экзаменационный билет у каждого студента может быть либо «счастливым» (этот исход обозначим буквой Ç), либо «несчастливым» (исход обозначим буквой Н). Тогда любой элементарный исход испытания может быть представлен парой букв, образованных из Ç и Н. Например, элементарный исход ÇН означает, что у 1-го студента «счастливый» билет, у 2-го – «несчастливый». Тогда множество всех возможных исходов испытания есть множество W = { ÇÇ, ÇН, НÇ, НН }. При таком построении пространства элементарных исходов W окажется, что
событие A = {студенты возьмут «счастливые» билеты} = { ÇÇ };
событие B = {первый студент возьмет «счастливый» билет} = { ÇÇ, Ç Н };
событие C = {только первый студент возьмет «счастливый» билет} = { ÇН }.
Однако события D и E невозможно описать однозначно при помощи элементов множества W. Если попытаться это сделать, например, положив D = { ÇН } и E = { ÇН }, то окажется, что три разных события С, D и E описаны совершенно одинаково. Очевидно, данный факт вызван неправильным построением пространства элементарных исходов W.
2-й способ. Из условия задачи видно, что экзаменационные билеты пронумерованы. На это указывают такие слова в тексте примера, как «… первые 10 билетов …», «… возьмет первый билет …», «… возьмет последний билет». Поэтому каждый билет можно отождествить с его номером и любой элементарный исход рассматриваемого испытания (это пара билетов) можно описать парой чисел (i, j), где i – номер билета у 1-го студента, j – номер билета у 2-го студента. Тогда пространства элементарных исходов есть множество
 и N = N (W) = 30´29 = 870.
и N = N (W) = 30´29 = 870.
Отметим, что в описании W номера i ¹ j, поскольку студенты не могут взять один и тот же билет.
Событие  , N (A) = 10´9 = 90;
, N (A) = 10´9 = 90;
событие B = N (B) =;
событие C = N (C) =;
событие D = N (D) =;
событие E = N (E) =.
Пример 1.9. В условиях примера 1.8 три студента поочередно и без возвращения берут по одному билету.
Пример 1.10. Некто решил покупать билеты моментальной лотереи до тех пор, пока ему не попадется выигрышный билет. Описать пространства элементарных исходов данного испытания и события, состоящие в том, что:
а) выиграет первый же билет; b) выиграет только пятый билет;
c) придется покупать не более пяти билетов; d) придется покупать не менее пяти билетов.
Решение. Испытание – покупка билетов моментальной лотереи до появления первого выигрышного билета. Пусть A, B, C и D – события, описанные в п.п. a) – d) соответственно. Обозначим буквой Β исход, состоящий в покупке выигрышного билета, буквой Н – невыигрышного билета. В данном примере пространство элементарных исходов является, в отличие от примеров 1.1 – 1.9, бесконечным:
W = { Β, НΒ, ННΒ, НННΒ, …, НН … НΒ, … }.
Событие A = N (A) =;
событие B = N (B) =;
событие C = N (C) =;
событие D =
Пример 1.11. В некотором регионе РФ проводится обследование возраста супругов. Наугад выбирается одна супружеская пара. Предполагая, что возраст супругов в данном регионе может быть от 16 до 120 лет, описать пространство элементарных исходов данного испытания и события, состоящие в том, что:
а) мужу не меньше 20 лет; b) жене не больше 20 лет; c) возраст супругов совпадает;
d) муж старше жены; e) возраст супругов отличается не более чем на 10 лет.
Решение. Испытание – выбор наугад супружеской пары в регионе РФ, где проводится обследование, и определение возраста супругов. Интересующие нас события, описанные в п.п. a) – e), обозначим через A, B, …, E соответственно. Каждый элементарный исход рассматриваемого испытания есть пара чисел, означающих возраст супругов. Дальнейшее решение возможно двумя способами, один из которых неверен.
1-й способ. Поскольку ситуация похожа на примеры 1.6 и 1.8 (там также элементарные исходы – это пары чисел), то попробуем строить пространство W аналогичным образом. Пусть i – возраст мужа, j – возраст жены, измеряемые в годах. Тогда в качестве пространства элементарных исходов можно взять множество  , состоящее из N (W) = 115´115 = 13 225 элементов. Однако очень многих исходов рассматриваемого испытания не будет в этом множестве W. Например, пары (20,5; 18), (35,3; 22,2), (45,5; 45,5) и т.д. не принадлежат W. Такое “обеднение” пространства W произошло, очевидно, из-за того, что возраст мы стали измерять в годах, т.е. в целых числах, хотя возраст – это физическая единица, измеряемая в годах, месяцах, днях, часах и т.д. Следовательно, неправильный выбор единицы измерения исходов испытания привел к неверному построению пространства элементарных исходов.
, состоящее из N (W) = 115´115 = 13 225 элементов. Однако очень многих исходов рассматриваемого испытания не будет в этом множестве W. Например, пары (20,5; 18), (35,3; 22,2), (45,5; 45,5) и т.д. не принадлежат W. Такое “обеднение” пространства W произошло, очевидно, из-за того, что возраст мы стали измерять в годах, т.е. в целых числах, хотя возраст – это физическая единица, измеряемая в годах, месяцах, днях, часах и т.д. Следовательно, неправильный выбор единицы измерения исходов испытания привел к неверному построению пространства элементарных исходов.
2-й способ. Пусть x – возраст мужа, y – возраст жены, измеряемые со сколь угодно высокой точностью. Иначе говоря, (x, y) – пара вещественных, а не только целых, чисел. Тогда в качестве пространства элементарных исходов можно взять множество
 ,
,
состоящее из бесконечного и несчетного числа элементов.
Событие  ; событие B =;
; событие B =;
событие C =; событие D =;
событие E =.
Пример 1.12. В условиях примера 1.11 изобразить на координатной плоскости пространство элементарных исходов W и события A, B, …, E.
Пример 1.13. Подбрасывается игральная кость. Обозначим события:
A = {выпадет шесть очков}; B = {выпадет три очка};
C = {выпадет четное число очков}; D = {выпадет число очков, кратное 3}.
a) Каковы отношения между этими событиями?
b) Описать события A + B; AB;  C \ D.
C \ D.
c) Образуют ли события A, B, C, D полную группу?
Решение. а) Так как AB = BC = Æ, AC = AD = CD = A, BD = B, то две пары событий из шести попарно несовместны, а остальные пары событий совместны. Далее, если выпадет шесть очков, то это означает, что выпадет и четное число очков, т.е. событие A влечет событие C: A Ì C. Рассуждая аналогично, получаем, что A Ì D и B Ì D.
b) События A + B = {3,6}; AB = Æ;  = W;
= W; 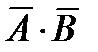 = {1,2,4,5}; C \ D = {2,4}.
= {1,2,4,5}; C \ D = {2,4}.
c) События A, B, C, D не образуют полную группу, так как A È B È C È D = {2, 3, 4, 6} ¹ W. Иначе говоря, в результате бросания игральной кости может выпасть, например, 5 очков, а такого исхода нет в группе событий A, B, C, D и, следовательно, нет в объединении этих событий A È B È C È D. g
Пример 1.14. Стрелок произвел три выстрела по мишени. Пусть событие Ak состоит в том, что произошло попадание при k -м выстреле (k = 1, 2, 3). Используя операции над событиями A 1, A 2, A 3, выразить следующие события:
A = {произошло три попадания}; B = {произошло три промаха};
C = {произошло попадание только при первом выстреле};
D = {произошло одно попадание}; E = {произошло хотя бы одно попадание};
F = {произошло не более одного попадания};
G = {произошло попадание в мишень после первого выстрела}.
Решение. Событие A = {(произошло попадание при 1-м выстреле) и (произошло попадание при 2-м выстреле) и (произошло попадание при 1-м выстреле)} = 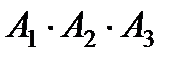 ;
;  ;
; 
 ; D = {(произошло попадание только при 1-м выстреле) или (произошло попадание только при 2-м выстреле) или (произошло попадание только при 3-м выстреле)} =
; D = {(произошло попадание только при 1-м выстреле) или (произошло попадание только при 2-м выстреле) или (произошло попадание только при 3-м выстреле)} =  ;
;
E = {(произошло 1 попадание) или (произошло 2 попадания) или (произошло 3 попадания)} =
F = {(не произошло ни одного попадания) или (произошло только одно попадание}} =
=
G =
Пример 1.15. Имеется три произвольных события A, B и C. Используя операции над этими событиями выразить следующие события:
a) произошло только событие A; b) произошли события A и B, но C не произошло;
c) произошли все три события; d) ни одно событие не произошло;
e) произошло только одно событие; f) произошли два события;
g) произошло не менее двух событий; h) произошло не более двух событий;
k) произошло по крайней мере одно событие.
Пример 1.16. Поражение боевого самолета может наступить или в результате поражения обоих двигателей (события A 1 и A 2), или в результате попадания в кабину пилота (событие B). Событие С означает поражение самолета. Выразите события С и  с помощью событий A и B 1, B 2.
с помощью событий A и B 1, B 2.
Пример 1.17. Испытание состоит в измерении размеров изображения на экране опытной модели телевизора, при котором фиксируется размер изображения по горизонтали и вертикали. До испытания было известно, что изображение на экране телевизора должно иметь размер по диагонали между 60 см и 75 см. Известно также, что размер изображения по горизонтали больше размера по вертикали, но не более, чем в 4/3 раза.
a) Описать пространство элементарных исходов испытания и следующие события:
A = {размер по горизонтали больше 50 см};
B = {размер по диагонали больше, чем 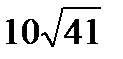 см};
см};
C = {размер по вертикали больше 40 см}.
b) Описать события AB, 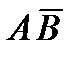 , A È B, (A \ C) È (C \ A).
, A È B, (A \ C) È (C \ A).
c) Показать, что BC Ì A.
1.18. Монета подбрасывается до тех пор, пока не выпадет герб. Описать пространство элементарных исходов.
1.19. Делается выстрел по квадратной мишени со стороной, равной 1. Описать пространство элементарных исходов.
1.20. Делается выстрел по круглой мишени радиуса 1. Описать пространство элементарных исходов.
1.21. Определить события  и
и  .
.
1.22. Являются ли совместными события  и
и 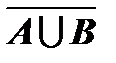 .
.
1.23. Доказать, что события  ,
,  ,
, 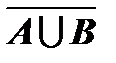 образуют полную группу событий.
образуют полную группу событий.
1.24. Докажите, что  .
.
1.25. Докажите, что  .
.
1.26. Докажите, что  .
.
1.27. Докажите, что  .
.
1.28. Докажите, что  .
.