Решение квадратных неравенств методом параболы

Задания 4, 8, 21. Уравнения, неравенства и их системы

Пропорция

Отношение – это частное двух чисел.

Пропорция – равенство двух отношений.

Основное свойство пропорции:

Произведение крайних членов пропорции равно произведению ее средних членов.

Пример: Найти неизвестный член пропорции х: 20 = 2: 5.

Решение: х и 5 — крайние члены пропорции, а 20 и 2 — средние.

5·х = 20·2 — применяем основное свойство пропорции;

х = 40:5 — произведение средних членов делим на известный крайний член;

х = 8 — получили искомый крайний член пропорции.

Уравнения

Уравнение – это буквенное равенство, которое справедливо только при некоторых значениях входящих в него букв.

Эти буквы называются неизвестными (переменными), а их значения, при которых данное уравнение обращается в верное равенство – корнями уравнения.

Решить уравнение – значит найти все его корни или доказать, что корней нет.

Равносильные уравнения – уравнения, у которых одинаковое решение

Основные тождественные преобразования (свойства уравнений)

Перенос слагаемых из одной части уравнения в другую со сменой знака.

12x – 4 = 15x – 10

 

12х – 15х = – 10 +4

Умножение или деление обеих частей уравнения на одно и то же число (выражение), отличное от нуля.

· 2

5х – 6 = 2х

3. Замена одного выражения другим, тождественно равным ему.

(3x+ 2)² = 15x+10

9x² + 12x + 4 = 15x + 10

Линейное уравнение с одной переменной

Общий вид линейного уравнения: ax + b = 0, где а и b – любые числа.

Решение линейных уравнений предполагает использование тождественных преобразований уравнений.

Пример: 3(х – 2) = 10 – (х – 5) - раскроем скобки

3х – 6 = 10 – х + 5 - перенесем слагаемые с х в одну часть, без х в другую

3х + х = 15 + 6 - приведем подобные слагаемые

4х = 21 - обе части уравнения разделим на 4

х = 5,25

Квадратное уравнение

Общий вид квадратного уравнения: + bx + c = 0, где a, b, c – числа, x – переменная. Если a = 0, то уравнение становится линейным. Поэтому, говоря о квадратных уравнениях, предполагается, что a ≠ 0.

Если коэффициент а = 1, то квадратное уравнение называют приведенным.

Квадратные уравнения

Полные (a ≠ 0, b ≠ 0, c ≠ 0) Неполные

+ bx + c = 0

+ bx = 0 (с = 0) + с = 0 (b = 0) = 0 (b = 0, с = 0)

Решение квадратных уравнений

1. В общем случае корни находятся через дискриминант D = b² – 4ac.

® Если D> 0, то уравнение имеет 2 корня:

® Если D = 0, то уравнение имеет 1 корень:

® Если D< 0, то уравнение не имеет корней.

2. Если коэффициент b четный, то можно найти = .

Тогда корни находятся по формуле: .

3. Если уравнение приведенное, то можно использовать т. Виета:

Сумма корней приведенного квадратного уравнения + bx + c = 0 равна коэффициенту перед х, взятому с противоположным знаком, а произведение равно свободному члену.

+ = – b

· = c

4. Неполные квадратные уравнения принято решать не через дискриминант.

+ bx = 0 (с = 0)	+ с = 0 (b = 0)	= 0 (b = 0, с = 0)
х2 – 2х = 0 х(х – 2) = 0 х = 0 или х – 2 = 0 х = 2	х2 – 4 = 0 х2 = 4 х = ± 2	4х2 = 0: 4 х2 = 0 х = 0

Дробно-рациональные уравнения

1. Найти общий знаменатель дробей;

2. Умножить обе части уравнения на общий знаменатель;

3. Решить получившееся целое уравнение;

4. Найти область допустимых значений (ОДЗ), исключив числа, при которых знаменатель обращается в 0.

5. В ответ записываются все корни, кроме тех, которые не удовлетворяют ОДЗ.

Пример: ∙x(x-5) - умножим дроби на общий знаменатель

x(x-3) + x – 5 = x + 5 ОДЗ: х(х-5) ≠ 0

х² – 3x – 10 = 0 x≠ 0 и х – 5 ≠ 0

x₁ = -2; x₂ = 5 х ≠ 5

Ответ: -2

Решение неравенств

Решить неравенство – значит найти границы, внутри которых должны находиться переменные, так чтобы неравенство было верным.

Линейные неравенства

Общий вид линейного неравенства: aх + b < 0 (знак неравенства может быть другим), где a и b – числа, х – неизвестная.

Линейные неравенства решаются с опорой на свойства, аналогично линейным уравнениям. Помним, если было произведено умножение или деление обеих частей неравенства на отрицательное число, то знак неравенства меняется на противоположный. В отличии от уравнений в ответ выписывается не конкретный набор чисел, а числовой промежуток.

Пример:

 

 

 

 

Ответ: х (- )

Квадратные неравенства

Общий вид квадратного неравенства: ах² + bх + с < 0 (знак неравенства может быть другим), где a, b и с – числа, х – неизвестная.

Для решения квадратных неравенств, есть 2 подхода (метод параболы и метод интервалов).

Решение квадратных неравенств методом параболы

Алгоритм:

ах² + bх + с < 0 (ах² + bх + с > 0)

1. Найти корни квадратного трехчлена ах² + bх + с, для этого решаем квадратное уравнение ах² + bх + с = 0.

2. Определить, куда направлены ветви параболы

3. Отметить найденные корни на оси х (если неравенство строгое, то точки выколоты).

4. Схематично изобразить график.

5. Определить, для каких х ординаты графика отрицательны (положительны).

Другими словами: для каких х график функции находится ниже (выше) оси х.

6. Выписать промежуток в ответ.

Пример: х² + х – 6 ≥ 0

▫ х² + х – 6 = 0

х₁ = -3, х₂ = 2

▫ у = х² + х – 6

коэффициент а=1 > 0 => ветви вверх

находим часть параболы, которая выше оси х

Ответ: ( ]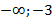

Решение квадратных неравенств методом интервалов.

Алгоритм:

1) Преобразовать неравенство таким образом, чтобы в правой части остался 0.

2) Разложить выражение в левой части на множители.

3) Приравнять это выражение к 0 и решить получившееся уравнение.

Замечание: если уравнение дробно-рациональное, не забываем найти ОДЗ.

4) Полученные корни отметить на координатной прямой (если знак неравенства строгий – точки выколоты, если нестрогий – закрашены).

Замечание: если уравнение дробно-рациональное, то точки, не вошедшие в ОДЗ выкалываем на координатной прямой.

5) Отмеченные точки разбивают координатную прямую на промежутки.

Берем любое число из каждого промежутка, подставляем вместо х в разложенное на множители выражение (п.2) и определяем знак этого выражения.

Над каждым промежутком подписываем этот знак.

6) В ответ берутся те промежутки, которые соответствуют знаку неравенства («+» соответствует >0, «–» соответствует <0)

Пример 1: (х + 3)(х – 2) ≥ 0

+

+

(х + 3)(х – 2) = 0

х = -3, х = 2

Ответ: ()

- перенесем 2 в левую часть неравенства - приведем к общему знаменателю - вычтем дроби - разложим на множители выражение слева (в числителе применяем формулу «квадрат разности») - находим нули числителя и знаменателя - отмечаем на координатной прямой точку 1 (закрашена) и точку 0 (выколота) - получилось 3 промежутка, берем из каждого любое число и подставляем в выражение (х-1)2, везде получается знак +

Пример 2:

х = 1

 

 

Знак неравенства , это значит, что в ответ пойдут промежутки со знаком «–» и точки, отмеченные на оси. Видим, что промежутков со знаком «–» нет и есть всего одна закрашенная точка на оси. Она и идет в ответ.

Ответ: 1

Системы уравнений

 

 

Пару чисел (х; у), которая одновременно является решением и первого, и второго уравнения системы, называют решением системы уравнений.

Решить систему – значит найти все ее решения или установить, что решений нет.