Прямое и обратное преобразование Гильберта.

Балтийский федеральный университет имени И. Канта

Физико-технический факультет

 

Утверждаю

Заведующий кафедры

к.т.н., доцент

А. Шпилевой

«___»_________ 200__ г.

 

 

Л Е К Ц И Я № 10

Тема: «Узкополосные случайные процессы»

Текст лекции по дисциплине: «Теория электрической связи»

 

Обсуждена и одобрена на заседании кафедры

протокол №___ от «___»___________200__г.

 

 

Г. Калининград 2012 г.

Текст лекции № 9

по дисциплине: «Теория электрической связи»

 

Введение

Для многих практических приложений бывает полезно представить сигнал в виде процесса с изменяющейся амплитудой и полной фазой. Такое представление процесса существенно упрощает построение аппаратуры, позволяет качественно решать многие вопросы передачи сигналов. Материал данной лекции необходим для понимания принципов построения демодуляторов. В дисциплине ТЭС также находят применение основные положения теории узкополосных процессов. В современных сотовых системах связи рассматриваемый сегодня принцип также находит широкое применение.

 

Квазигармоническая форма представления сигнала

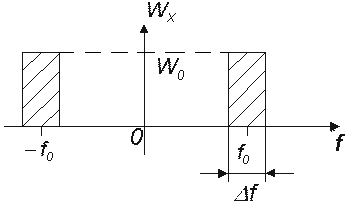
К узкополосным случайным процессам относят процессы, спектральная плотность мощности которых сосредоточена в относительно узкой полосе частот в окрестности некоторой достаточно высокой частоты f₀ (рисунок 1.1), то есть D f<<f₀.

 

Рисунок 1.1 – Узкополосный случайный процесс

 

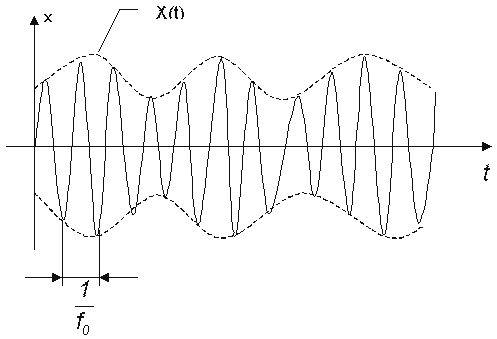
Пример реализации такого случайного процесса показан на рисунке 1.2, где C (t) – огибающая.

 

Рисунок 1.2 – Пример реализации типового случайного процесса

 

Во многих случаях сигнал x(t) удобно записывать в квазигармонической форме в виде:

 

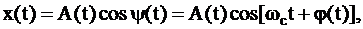
	(1.1)
где		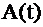–	огибающая;
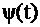
		–	полная фаза;
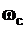
		–	средняя частота квазигармонического колебания;
	j(t)	–	медленно изменяющаяся начальная фаза.

 

Для определения A(t) и y(t) введем в рассмотрение комплексный сигнал 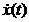, получаемый из действительного сигнала x(t) следующим образом:

 

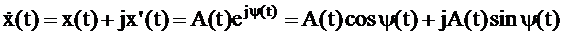
	(1.2)
где		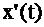–	называют сопряжённым сигналом (связанным некоторым образом с x(t)).

 

Тогда:

 

(1.3)

 

Поскольку сопряжённый x’(t) сигнал можно связать с исходным x(t) разными способами, то задача вычисления огибающей и полной фазы оказывается неоднозначной.

 

Вывод:

1.Квазигармоническая форма представления сигнала удобна для построения демодуляторов.

 

Прямое и обратное преобразование Гильберта.

 

По ряду причин, часть из которых станет понятной из дальнейшего, в качестве сопряжённого удобно выбрать преобразованный по Гильберту исходный сигнал:

 

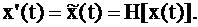
(1.4)

 

Комплексный сигнал вида 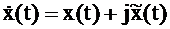называют аналитическим сигналом.

Преобразование Гильберта H[x(t)] в спектральной области сводиться к сдвигу фаз всех спектральных составляющих сигнала x(t) на угол 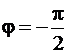в области положительных (ω>0) и на в 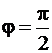области отрицательных (ω<0) частот.

С точки зрения схемотехники преобразователь Гильберта – это фазовращатель (рисунок 1) с передаточной функцией, которая представлена следующим выражением:

 

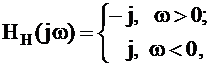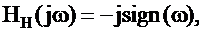
	(1.5)
где		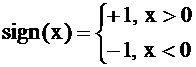–	знаковая функция.

 

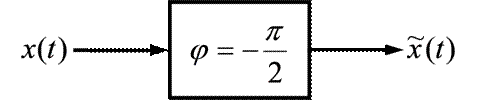
Рисунок 1.3 – Преобразователь Гильберта

 

Найдём импульсную характеристику преобразователя Гильберта

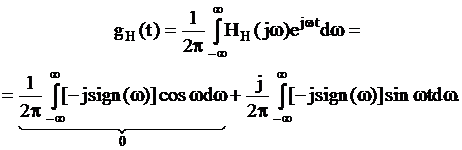
Первый интеграл в полученном выражении равен 0 в силу интегрирования нечётной функции при симметричных пределах, а второй сводиться к табличному интегралу вида:

 

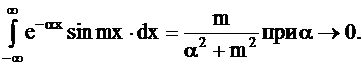
(1.6)

 

Окончательно получаем:

 

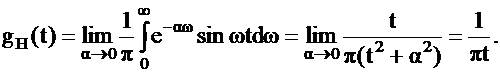
(1.7)

 

Из полученного результата с очевидностью вытекает невозможность физической реализации преобразования Гильберта, так как 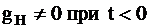. Тем не менее, реально преобразования Гильберта осуществляют приближённо, допуская временную задержку, тем большую, чем выше требования к точности преобразования.

Рассмотрим преобразование Гильберта во временной области. Из рисунка 1.3 вытекает:

 

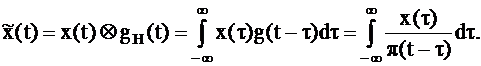
	(1.8)
где		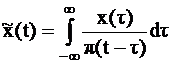–	прямое преобразование Гильберта.

 

Поскольку

 

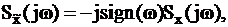
(1.9)

 

после умножения обеих частей равенства на jsign(w) получим

 

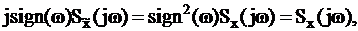
(1.10)

 

откуда следует, что передаточная функция обратного преобразования Гильберта H^-1[x(t)] отличается от передаточной функции прямого только знаком:

 

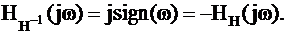
(1.11)

 

Соответственно:

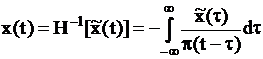– обратное преобразование Гильберта.