Пусть дана система линейных уравнений:

Запишем заданную систему в матричном виде:
 , где
, где
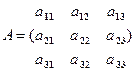


Если матрица  невырождена, то тогда с помощью операций над матрицами выразим неизвестную матрицу
невырождена, то тогда с помощью операций над матрицами выразим неизвестную матрицу 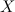 . Операция деления на множестве матриц заменена умножением на обратную матрицу, поэтому домножим последнее равенство на матрицу
. Операция деления на множестве матриц заменена умножением на обратную матрицу, поэтому домножим последнее равенство на матрицу  слева:
слева:


Поэтому, чтобы найти неизвестную матрицу 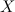 надо найти обратную матрицу к матрице системы и умножить ее справа на вектор-столбец свободных коэффициентов.
надо найти обратную матрицу к матрице системы и умножить ее справа на вектор-столбец свободных коэффициентов.
Пример
Задание. Решить с помощью обратной матрицы систему 
Решение. Запишем данную систему в матричной форме:
 ,
,
где  - матрица системы,
- матрица системы,  - столбец неизвестных,
- столбец неизвестных,  - столбец правых частей. Тогда
- столбец правых частей. Тогда

Найдем обратную матрицу  к матрице
к матрице  с помощью союзной матрицы:
с помощью союзной матрицы:

Здесь  - определитель матрицы
- определитель матрицы  ; матрица
; матрица  - союзная матрица, она получена из исходной матрицы
- союзная матрица, она получена из исходной матрицы  заменой ее элементов их алгебраическими дополнениями. Найдем
заменой ее элементов их алгебраическими дополнениями. Найдем  , для этого вычислим алгебраические дополнения к элементам матрицы
, для этого вычислим алгебраические дополнения к элементам матрицы  :
:





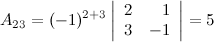



Таким образом,

Определитель матрицы 


А тогда

Отсюда искомая матрица


Ответ. 
Метод Крамера
Теорема Крамера. Если определитель матрицы квадратной системы не равен нулю, то система совместна и имеет единственное решение, которое находится по формулам Крамера:

где 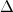 - определитель матрицы системы,
- определитель матрицы системы,  - определитель матрицы системы, где вместо
- определитель матрицы системы, где вместо 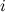 -го столбца стоит столбец правых частей.
-го столбца стоит столбец правых частей.
Замечание
Если определитель системы равен нулю, то система может быть как совместной, так и несовместной.
Замечание
Данный метод удобно применять для маленьких систем с громоздкими вычислениями, а так же если нужно найти одну из неизвестных. Трудность заключается в том, что необходимо считать много определителей.
Примеры решения систем уравнений методом Крамера

Решение. Вычисляем определитель матрицы системы:


Так как определитель матрицы системы неравен нулю, то по теореме Крамера система совместна и имеет единственное решение. Для его нахождения вычислим следующие определители:




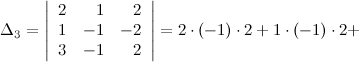

Таким образом,



Ответ. 
Метод Гаусса (метод последовательного исключения неизвестных)
При решении систем линейных уравнений используют также метод Гаусса. Он состоит в следующем: систему уравнений приводят к эквивалентной ей системе с треугольной матрицей (системы называются эквивалентными, если множества их решений совпадают). Эти действия называют прямым ходом. Из полученной треугольной системы переменные находят с помощью последовательных подстановок(обратный ход).
При выполнении прямого хода используют следующие преобразования:
· умножение или деление на одно и то же число;
· сложение и вычитание уравнений;
· перестановку уравнений системы;
· исключение из системы уравнений, в которых все коэффициенты при неизвестных и свободные члены равны нулю.