Пусть функция f (x) непрерывна на замкнутом интервале [ a, b ]. Если F (x) – п ервообраз-ная функции f (x) на[ a, b ], то

Площадь криволинейной трапеции
Площадь фигуры, ограниченной осью 0 x, двумя вертикальными прямыми x = a, x = b и графиком функции f (x) (рисунок 1), определяется по формуле

|
Пусть F (x) и G (x) - первообразные функций f (x) и g (x), соответственно. Если f (x) ≥ g (x) на замкнутом интервале [ a, b ], то площадь области, ограниченной двумя кривыми y = f (x), y = g (x) и вертикальными линиями x = a, x = b (рисунок 2), определяется формулой

Замена переменной в определенном интеграле
Определенный интеграл  переменной x можно преобразовать в определенный интеграл относительно переменной t с помощью подстановки x = g (t):
переменной x можно преобразовать в определенный интеграл относительно переменной t с помощью подстановки x = g (t):

Новые пределы интегрирования по переменной t определяются выражениями

где g -1 - обратная функция к g, т.е. t = g -1(x).
Интегрирование по частям для определенного интеграла
В этом случае формула интегрирования по частям имеет вид:

где  означает разность значений произведения функций uv при x = b и x = a.
означает разность значений произведения функций uv при x = b и x = a.
Пример 1. Вычислить интеграл  .
.
Решение.
Применяя формулу Ньютона-Лейбница, получаем

Пример 2. Вычислить интеграл  .
.
Решение.

Пример 3. Вычислить интеграл  .
.
Решение.
Сделаем замену:

Пересчитаем пределы интегрирования. Если x = 0, то t = −1. Если же x = 1, то t = 2. Тогда интеграл через новую переменную t легко вычисляется:

Пример 4. Вычислить интеграл  .
.
Решение.
Запишем интеграл в виде

Используем интегрирование по частям:  . В нашем случае пусть будет
. В нашем случае пусть будет

Следовательно, интеграл равен

Пример 5. Найти площадь фигуры, ограниченной кривыми  и
и  .
.
Решение.
 Построим графики кривых.
Построим графики кривых.
Определим точки пересечения двух кривых:
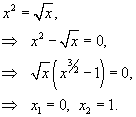
Таким образом, данные кривые пересекаются в точках (0,0) и (1,1). Следовательно, площадь фигуры равна

Пример 6. Найти площадь фигуры, ограниченную графиками функций  и
и  .
.

Решение.
Найдем координаты точек пересечения кривых.

Данная область ограничивается сверху параболой  , а снизу - прямой линией
, а снизу - прямой линией  . Следовательно, площадь этой области равна
. Следовательно, площадь этой области равна

Приложения
Практическая работа №1 « Решение систем линейных уравнений методом обратной матрицы, Крамера, Гаусса. Действия с комплексными числами.»
№№ 1-20. Решите систему линейных уравнений тремя способами:
1) методом Крамера,
2) методом Гаусса,
3) методом обратной матрицы (матричным методом).

| 
| ||

| 
| ||

| 
| ||

| 
| ||
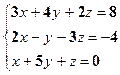
| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
|
Практическая работа №2 « Вычисление пределов функции. Применение производной к исследованию функции.. »
2 №№ 21-40. Вычислите пределы, не пользуясь правилом Лопиталя.
a) 
| 
| 
| |

| 
| 
| |

| 
| 
| |

| 
| 
| |

| 
| 
| |

| 
| 
| |

| 
| 
| |

| 
| 
| |
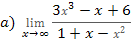
| 
| 
| |

| 
| 
| |

| 
| 
| |

| 
| 
| |

| 
| 
| |
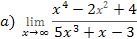
| 
| 
| |

| 
| 
| |

| 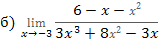
| 
| |

| 
| 
| |

| 
| 
| |

| 
| 
| |

| 
| 
|
№№ 41-60. Найдите производные функций.

| 
| 
| 
| |

| 
| 
| 
| |

| 
| 
| 
| |
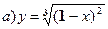
| 
| 
| 
| |

| 
| 
| 
| |

| 
| 
| 
| |

| 
| 
| 
| |

| 
| 
| 
| |

| 
| 
| 
| |

| 
| 
| 
| |

| 
| 
| 
| |
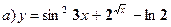
| 
| 
| 
| |

| 
| 
| 
| |

| 
| 
| 
| |

| 
| 
| 
| |

| 
| 
| 
| |

| 
| 
| 
| |
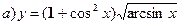
| 
| 
| 
| |

| 
| 
| 
| |

| 
| 
| 
|
№№61-80. Исследовать функции методами дифференциального исчисления и построить их графики.

| 
| |

| 
| |

| 
| |
 2 2
| 
| |

| 
| |

| 
| |

| 
| |

| 
| |

| 
| |

| 
| |

| 
| |

| 
| |

| 
| |

| 
| |

| 
| |

| 
| |

| 
| |

| 
| |

| 
| |

| 
|
Практическая работа № 3 « Неопределенный интеграл.Методы нахождения неопределенного интеграла. Определенный интеграл.Приложение определенного интеграла к решению прикладных задач.»
№№ 81-100. Найдите неопределенные интегралы.

| б) 
| |

| б) 
| |

| б) 
| |

| б) 
| |

| б) 
| |

| б) 
| |

| б) 
| |

| б) 
| |

| б) 
| |

| б) 
| |

| б) 
| |

| б) 
| |

| б) 
| |

| б) 
| |

| б) 
| |

| б) 
| |

| б) 
| |

| б) 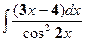
| |
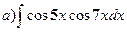
| б) 
| |

| б) 
|
№№ 101-120. Вычислите определенные интегралы.
а) 
| б) 
| |
а) 
| б) 
| |
а) 
| б) 
| |
а) 
| б) 
| |
а) 
| б) 
| |
а) 
| б) 
| |
а) 
| б) 
| |
а) 
| б) 
| |
а) 
| б) 
| |
а) 
| б) 
| |
а) 
| б) 
| |
а) 
| б) 
| |
а) 
| б) 
| |
а) 
| б) 
| |
а) 
| б) 
| |
а) 
| б) 
| |
а) 
| б) 
| |
а) 
| б) 
| |
а) 
| б) 
| |
а) 
| б) 
|
№№121-126. Вычислите площадь фигуры, ограниченной линиями. Постройте графики.
 и и 
| 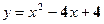 и и 
| ||
 и и 
|  и и 
| ||
 и и 
|  и и 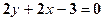
|
127. Вычислите площадь фигуры, ограниченную одной волной синусоиды  . Постройте график.
. Постройте график.
128. Вычислите площадь фигуры, ограниченную одной волной косинусоиды  . Постройте график.
. Постройте график.
129. Вычислите площадь фигуры, ограниченную линиями: у=tgx, y=0,x=0,  . Постройте графики.
. Постройте графики.
№№130-140. Вычислите площадь фигуры, ограниченной линиями. Постройте графики.
| 130. |  и и 
| 135. |  и и 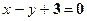
|
| 131. |  и и 
| 136. |  , ,  и и 
|
| 132. |  и и 
| 137. |  , х=0, х=5 и у=0 , х=0, х=5 и у=0
|
| 133. |  и и 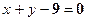
| 138. |  , х=0, у=0 и х=3 , х=0, у=0 и х=3
|
| 134. |  и и 
| 139. |  , , 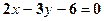 и у=0 и у=0
|
| 140. |  и у=0 и у=0
|
Практическая работа №4 «Элементы теории вероятностей. Дискретная и непрерывная случайные величины. Закон распределения случайной величины. По заданному условию построить закон распределения дискретной случайной величины»
№141-179. Задачи комбинаторики
Задача 141. В группе 30 студентов. Необходимо выбрать старосту, заместителя старосты и профорга. Сколько существует способов это сделать?
Задача142. Два почтальона должны разнести 10 писем по 10 адресам. Сколькими способами они могут распределить работу?
Задача 143. В ящике 100 деталей, из них 30 – деталей 1-го сорта, 50 – 2-го, остальные – 3-го. Сколько существует способов извлечения из ящика одной детали 1-го или 2-го сорта?
Задача 144. Фирма имеет три источника поставки комплектующих – фирмы А, B, С. На долю фирмы А приходится 50% общего объема поставок, В – 30% и С – 20%. Из практики известно, что среди поставляемых фирмой А деталей 10% бракованных, фирмой В – 5% и фирмой С – 6%. Какова вероятность, что взятая наугад деталь окажется годной?
Задача 145. Порядок выступления 7 участников конкурса определяется жребием. Сколько различных вариантов жеребьевки при этом возможно?
Задача 146. В конкурсе по 5 номинациям участвуют 10 кинофильмов. Сколько существует вариантов распределения призов, если по всем номинациям установлены различные премии?
Задача 147. В шахматном турнире участвуют 16 человек. Сколько партий должно быть сыграно в турнире, если между любыми двумя участниками должна быть сыграна одна партия?
Задача 148. В условиях задачи 6 определить, сколько существует вариантов распределения призов, если по всем номинациям установлены одинаковые призы?
Задача 149. Садовник должен в течении трех дней посадить 6 деревьев. Сколькими способами он может распределить по дням работу, если будет сажать не менее одного дерева в день?
Задача 150. Сколько существует четырехзначных чисел (возможно, начинающихся с нуля), сумма цифр которых равна 5?
Задача 151. Сколькими способами можно разбить группу из 25 студентов на три подгруппы А, В и С по 6, 9 и 10 человек соответственно?
Задача 152. Сколько существует семизначных чисел, состоящих из цифр 4, 5 и 6, в которых цифра 4 повторяется 3 раза, а цифры 5 и 6 – по 2 раза?
Задача 153. В ящике 5 апельсинов и 4 яблока. Наудачу выбираются 3 фрукта. Какова вероятность, что все три фрукта – апельсины?
Задача 154. Преподаватель предлагает каждому из трех студентов задумать любое число от 1 до 10. Считая, что выбор каждым из студентов любого числа из заданных равновозможен, найти вероятность того, что у кого-то из них задуманные числа совпадут.
Задача 155. Найти вероятность того, что в 8-значном числе ровно 4 цифры совпадают, а остальные различны.
Задача 156. Шесть клиентов случайным образом обращаются в 5 фирм. Найти вероятность того, что хотя бы в одну фирму никто не обратится.
Задача 157. Пусть в урне имеется N шаров, из них М белых и N–M черных. Из урны извлекается n шаров. Найти вероятность того, что среди них окажется ровно m белых шаров.
Задача 158. Точку наудачу бросили на отрезок [0; 2]. Какова вероятность ее попадания в отрезок [0,5; 1,4]?
Задача 159(задача о встрече). Два лица А и В условились встретиться в определенном месте между 12 и 13 часами. Пришедший первым ждет другого в течении 20 минут, после чего уходит. Чему равна вероятность встречи лиц А и В, если приход каждого из них может произойти наудачу в течении указанного часа и моменты прихода независимы?
Задача 160. В ящике 10 красных и 5 синих пуговиц. Вынимаются наудачу две пуговицы. Какова вероятность, что пуговицы будут одноцветными?
Задача 161. Среди сотрудников фирмы 28% знают английский язык, 30% – немецкий, 42% – французский; английский и немецкий – 8%, английский и французский – 10%, немецкий и французский – 5%, все три языка – 3%. Найти вероятность того, что случайно выбранный сотрудник фирмы: а) знает английский или немецкий; б) знает английский, немецкий или французский; в) не знает ни один из перечисленных языков.
Задача162. В семье – двое детей. Какова вероятность, что старший ребенок – мальчик, если известно, что в семье есть дети обоего пола?
Задача 163. Мастер, имея 10 деталей, из которых 3 – нестандартных, проверяет детали одну за другой, пока ему не попадется стандартная. Какова вероятность, что он проверит ровно две детали?
Задача 164. В одном ящике 3 белых и 5 черных шаров, в другом ящике – 6 белых и 4 черных шара. Найти вероятность того, что хотя бы из одного ящика будет вынут белый шар, если из каждого ящика вынуто по одному шару.
Задача 165. Три экзаменатора принимают экзамен по некоторому предмету у группы в 30 человек, причем первый опрашивает 6 студентов, второй — 3 студентов, а третий — 21 студента (выбор студентов производится случайным образом из списка). Отношение трех экзаменаторов к слабо подготовившимся различное: шансы таких студентов сдать экзамен у первого преподавателя равны 40%, у второго — только 10%, у третьего — 70%. Найти вероятность того, что слабо подготовившийся студент сдаст экзамен.
Задача 166. Фирма имеет три источника поставки комплектующих – фирмы А, B, С. На долю фирмы А приходится 50% общего объема поставок, В – 30% и С – 20%. Из практики известно, что среди поставляемых фирмой А деталей 10% бракованных, фирмой В – 5% и фирмой С – 6%. Какова вероятность, что взятая наугад деталь окажется годной?
Задача 167 (см. задачу 6). Пусть известно, что студент не сдал экзамен, т.е. получил оценку «неудовлетворительно». Кому из трех преподавателей вероятнее всего он отвечал?
Задача 168. Игральная кость брошена 6 раз. Найти вероятность того, что ровно 3 раза выпадет «шестерка».
Задача 169. Монета бросается 6 раз. Найти вероятность того, что герб выпадет не более, чем 2 раза.
Задача 170. Аудитор обнаруживает финансовые нарушения у проверяемой фирмы с вероятностью 0,9. Найти вероятность того, что среди 4 фирм-нарушителей будет выявлено больше половины.
Вариант 171
Производится три независимых опыта, в каждом из которых событие А появляется с вероятностью 0,4. Рассматривается случайная величина X – частота появления события А в трёх опытах. Найдите закон распределения случайной величины X.
Вариант 172
При разыгрывании некоторой лотереи наудачу покупается три билета. Рассматривается случайная величина X – число выбранных билетов с выигрышем. Вероятность выигрыша на каждый билет равна 0,2. Найдите закон распределения случайной величины X.
Вариант 173
Из партии деталей наудачу отбирают 3 детали. Рассматривается случайная величина X – число выбранных нестандартных деталей. Найдите закон распределения случайной величины X, если вероятность того, что деталь окажется нестандартной, равна 0,1.
Вариант 174
В ящике находятся белые и чёрные шары. Из ящика наудачу вынимаются 4 шара. Рассматривается случайная величина X – количество появления белых шаров. Найдите закон распределения случайной величины X, если вероятность появления белого шара равна 0,4.
Вариант 175
По мишени производится 4 выстрела, причём вероятность промаха при каждом выстреле равна 0,01. Рассматривается случайная величина X – количество промахов по мишени. Найдите закон распределения случайной величины X.
Вариант 186
Рыбак забросил спиннинг 3 раза, причём вероятность того, что рыбак поймал рыбу, при каждом забрасывании равна 0,6. Рассматривается случайная величина X – число пойманных рыб. Найдите закон распределения.
Вариант 187
Монета подбрасывается 5 раз. Рассматривается случайная величина X – число появлений «решётки». Найдите закон распределения случайной величины X.
Вариант 188
Из партии изделий наудачу выбираются 3 изделия. Рассматривается случайная величина X – количество выбранных изделий с браком. Найдите закон распределения случайной величины X, если вероятность появления брака равна 0,6.
Вариант 189
Имеются три лампы, каждая из которых с вероятностью 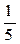 имеет дефект. При ввинчивании в патрон дефектная лампа сразу перегорает, и тогда ввинчивается следующая. Рассматривается случайная величина X – число ввинченных ламп. Найдите закон распределения случайной величины X.
имеет дефект. При ввинчивании в патрон дефектная лампа сразу перегорает, и тогда ввинчивается следующая. Рассматривается случайная величина X – число ввинченных ламп. Найдите закон распределения случайной величины X.
Вариант 190
При разыгрывании некоторой лотереи наудачу покупается пять билетов. Рассматривается случайная величина X – число выбранных билетов с выигрышем. Вероятность выигрыша на каждый билет равна 0,01. Найдите закон распределения случайной величины X.
Вариант 191
Рыбак забросил спиннинг 4 раза, причём вероятность того, что рыбак поймал рыбу, при каждом забрасывании равна  . Рассматривается случайная величина X – число пойманных рыб. Найдите закон распределения.
. Рассматривается случайная величина X – число пойманных рыб. Найдите закон распределения.
Вариант 192
Из урны, содержащей кубики и шары, наугад вынимается 4 предмета. Рассматривается случайная величина X – число появления кубиков. Найдите закон распределения случайной величины X, если вероятность появления кубиков равна  .
.
Вариант 193
Имеются четыре лампы, каждая из которых с вероятностью  имеет дефект. При ввинчивании в патрон дефектная лампа сразу перегорает, и тогда ввинчивается следующая. Рассматривается случайная величина X – число ввинченных ламп. Найдите закон распределения случайной величины X.
имеет дефект. При ввинчивании в патрон дефектная лампа сразу перегорает, и тогда ввинчивается следующая. Рассматривается случайная величина X – число ввинченных ламп. Найдите закон распределения случайной величины X.
Вариант 194
Из ящика наудачу вынимают 3 ламп

