Новый материал: Геометрическая интерпретация комплексных чисел

Тема урока «Комплексные числа».

Задание: Читаем теоретический материал, составляем конспект

«КОМПЛЕКСНЫЕ ЧИСЛА», решаем самостоятельную работу,

отправляем фотоотчёт конспекта и СР мне «Вконтакте» с указанием фамилии, названия работы, даты выполнения.

Комплексные числа.

Повторим определение комплексных чисел в алгебраической форме

Определение 1. Комплексным числом z называется выражение ви­да а+bi, a _{и b} —действительные числа, а символ i удовлетворяет условию i = - 1

Число а называется действительной частью комплексного числа, bi — мнимой частью, i — мнимой единицей.

Множество комплексных чисел обозначается буквой С.

Заметим, что множество R действительных чисел содержится в множестве комплексных чисел С: R 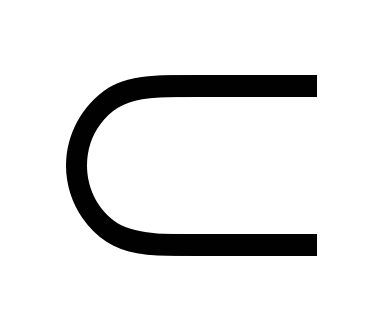C. В самом деле, всякое действительное число а можно рассматривать как комплексное число вида а+ 0 i.

Комплексные числа вида bi называют чисто мнимыми. Они по­лучаются из комплексных чисел z₁ = а + bi при а = 0.

Определение 2. Два комплексных числаz₁ = а + bi и z ₂ = с + di на­зываются равными, если, соответственно, равны их действительные части и коэффициенты при мнимой единице, т. е. если а = с, b = d.

Комплексное число z = 0 + 0 i называется нулем и обозначается че­рез 0. Оно совпадает с числом нуль множества действительных чисел. Таким образом, z = а + bi = 0 тогда и только тогда, когда а = 0 и b= 0, или, что то же самое, когда а ² + b ² = 0.

Определение 3. Комплексные числа а + bi и а — bi называются ком­плексно-сопряженными.

Число, комплексно-сопряженное числу z, обозначается через 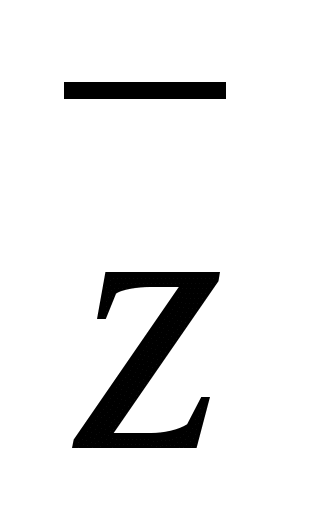. Так, если z = а + bi, то 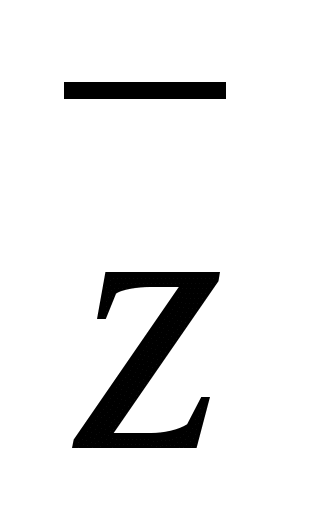= а — bi, если же z = а − bi, то 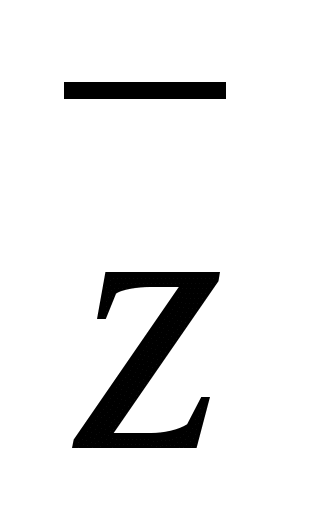= а + bi. По­нятие сопряженности взаимное. Например, для комплексного числа z = = -2 + 4 i комплексно-сопряженным является комплексное число 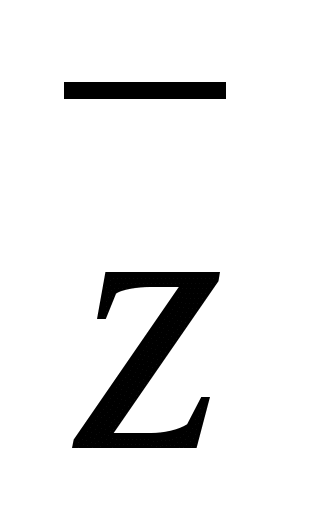= - 2 - 4 i; точно также для комплексного числа -2 - 4 i комплексно-со­пряженным является число -2 + 4 i.

Новый материал: Геометрическая интерпретация комплексных чисел

Комплексное число z = а + bi геометрически можно представить точкой координатной плоскости Оху с координатами а, b (рис. 1).

Определение 4. Плоскость, служащая для изображения множества комплексных чисел, называется комплексной плоскостью. Так как любое комплексное число единственным образом определяется его действительной и мни­мой частями, то каждому комплексному числу в комплексной плоскости соответствует единственная точка на плоскости. Очевидно, что справедливо и обратное утверждение: каждой точке(х; у)плоскости Оху соответствует единственное комплексное число z = х + yi.

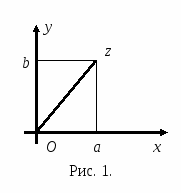
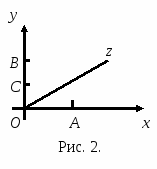
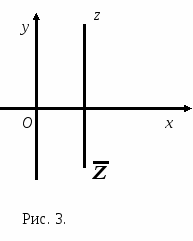
Таким образом, между множеством комплексных чисел и множеством точек плоскости существует взаимно-однозначное соответствие. При этом соответствии всякому действительному числу z = а + 0 i соответствует точка А (а;0) оси абсцисс, а всякому чисто мнимому числу z = 0 + bi — точка В(0; b) оси ординат. Числу z = i соответствует точка С(0; 1) (рис. 2). Если каждой точке М комплексной плоскости поставить в соответствие радиус-вектор ОМ этой точки, между множеством комплексных чисел множеством радиус-векторов можно также установить взаимно-однозначное соответствие. Ось Ох будем называть действительной осью, а ось Оу — мнимой.

Из определения комплексно-сопряженных чисел следует, что числа z и 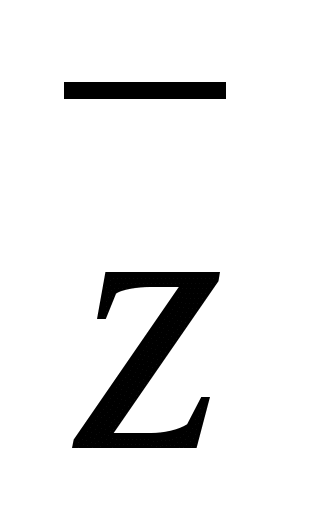на комплекс­ной плоскости расположены симметрично от­носительно действительной оси (рис. 3).

Ранее мы отметили, что квадратное уравнение ax ² + bx + c = 0, для которого дискриминант D = b ² – 4ас < 0, в множестве R (действительных чисел) не имеет решения, так как корень из отрицательного числа в этом множе­стве не имеет действительного значения. Однако в множестве С (ком­плексных чисел) такое уравнение имеет два комплексно-сопряженных решения. В самом деле, пусть дано квадратное уравнение

ах ² + bx + c = 0_.

причем D < 0.

Решения этого уравнения

_,

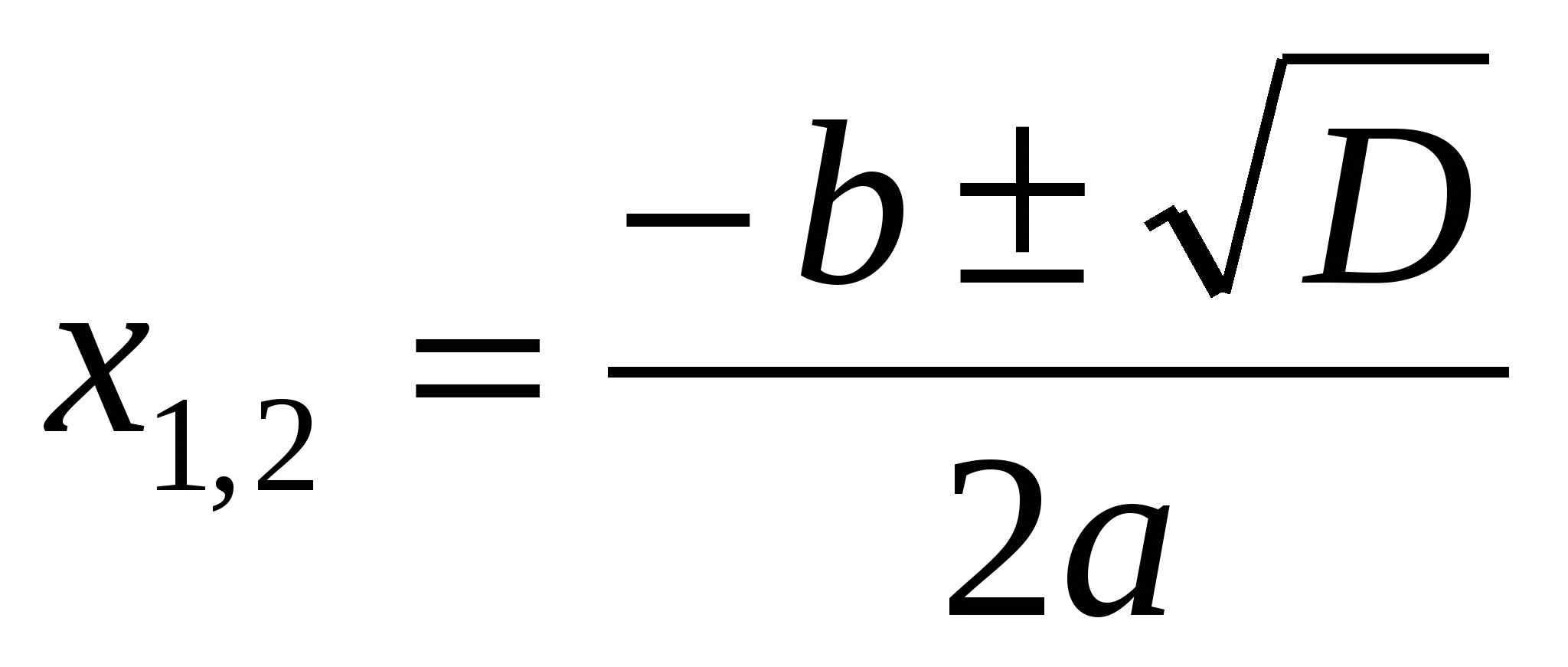представим в виде

,

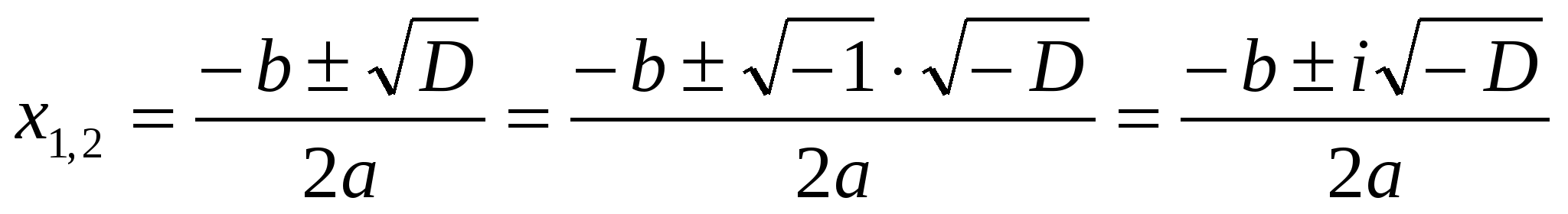где уже 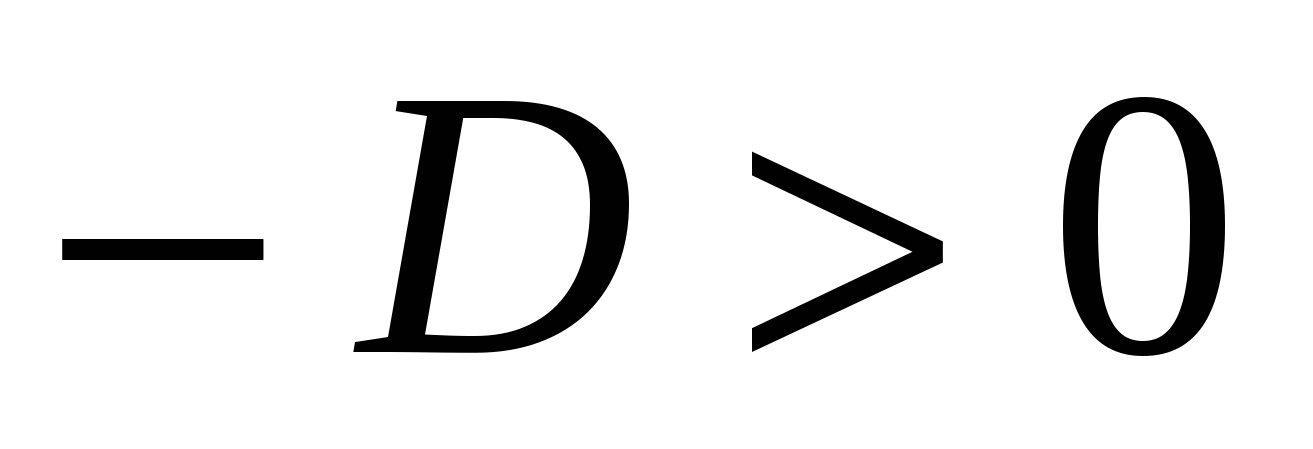, а потому 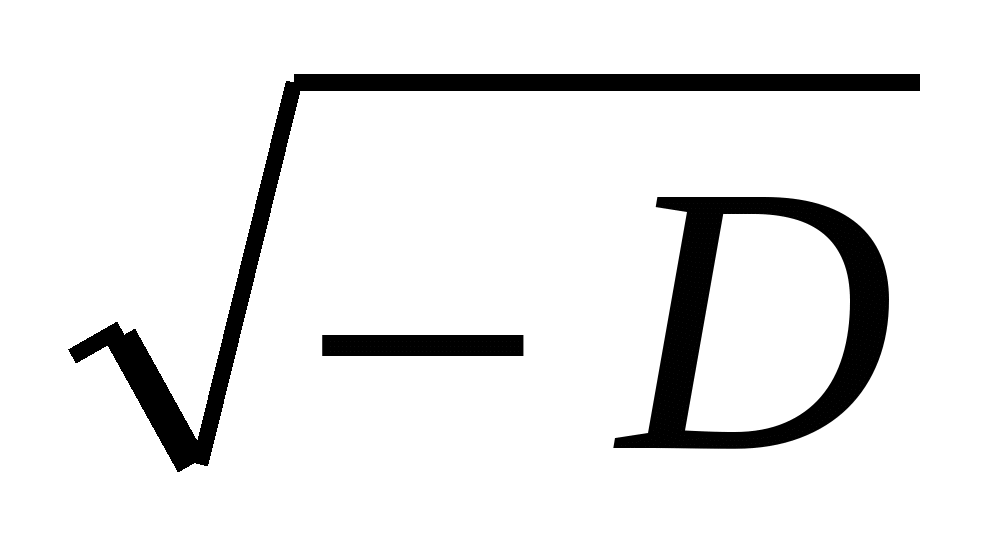есть некоторое действительное число.

Следовательно, решениями квадратного уравнения будут два комплекс­но-сопряженных числа

, .

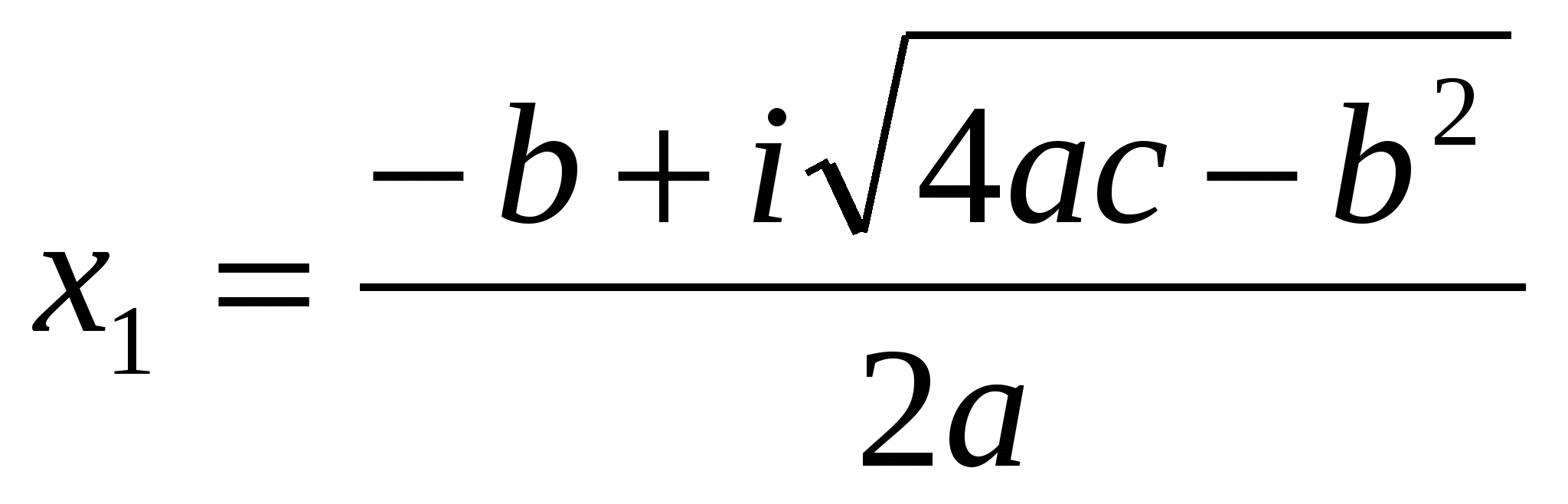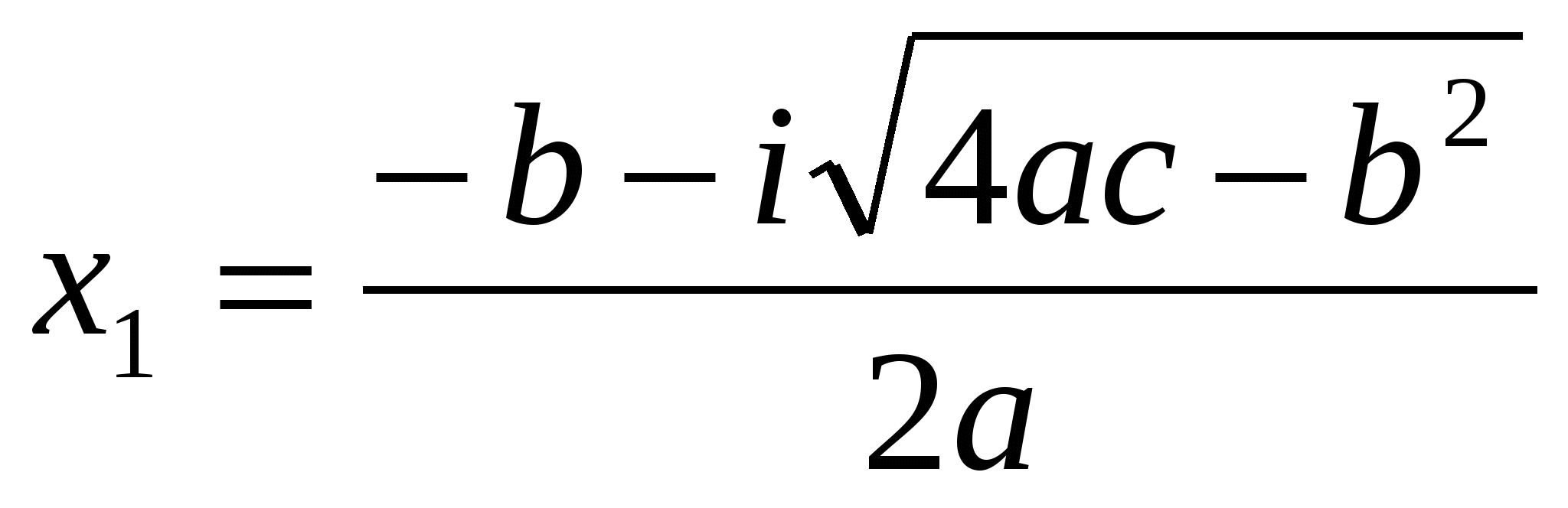Пример 1. Решить квадратное уравнение .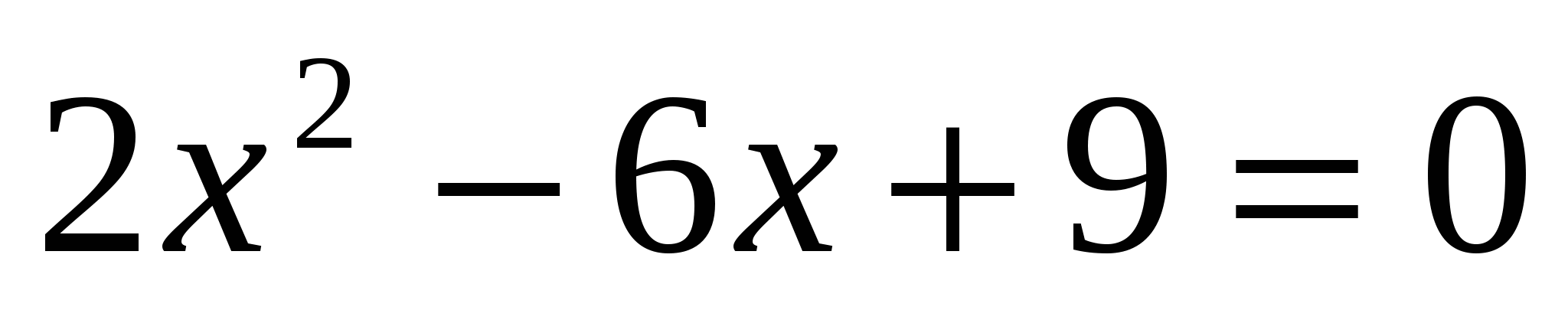

Решение. Находим:

_.

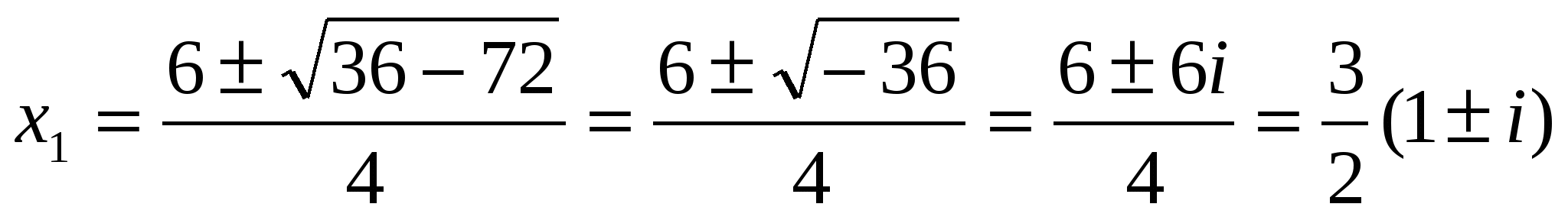Таким образом, решениями данного квадратного уравнения будут два комплексно-сопряженных числа

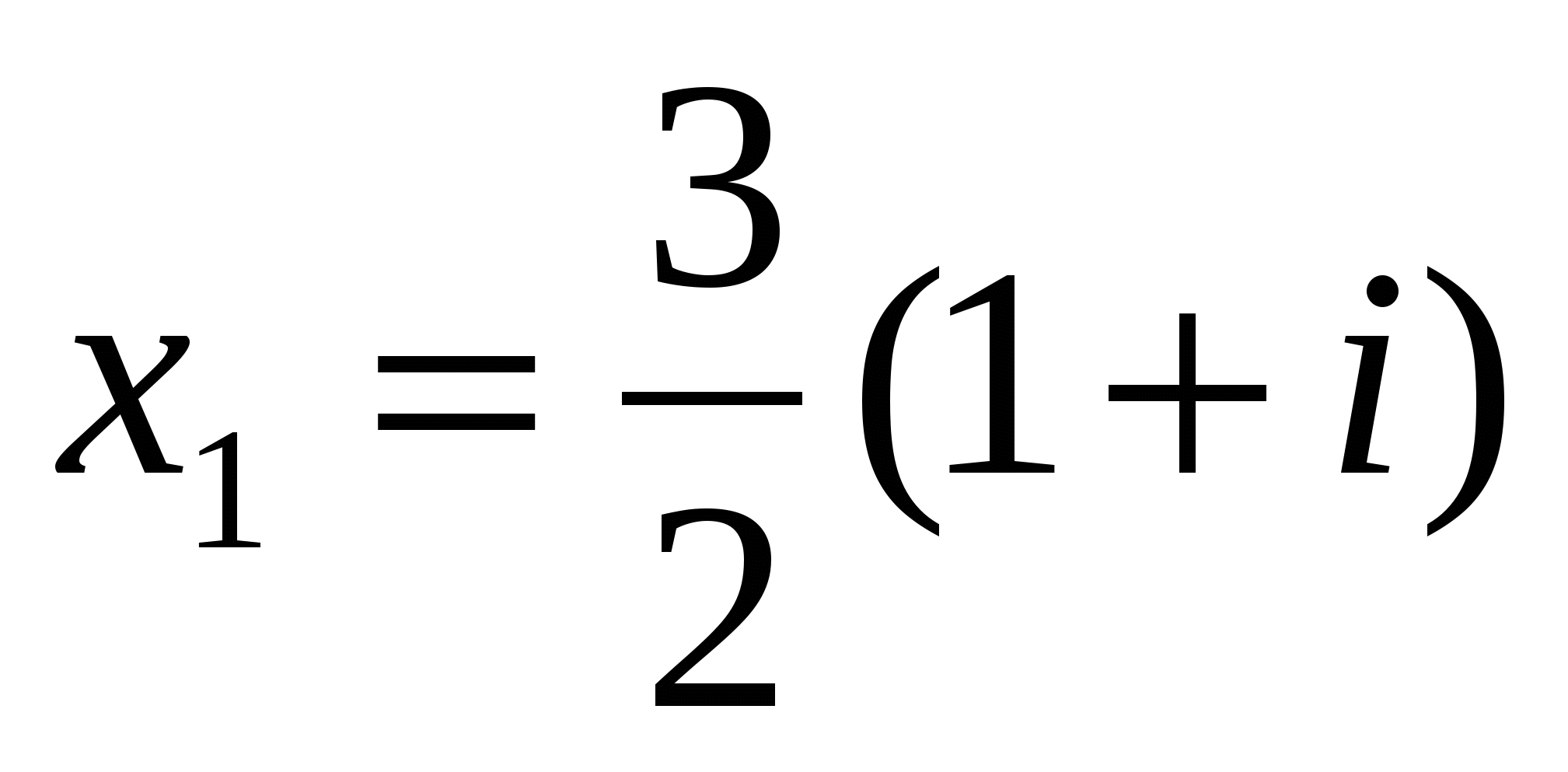и _.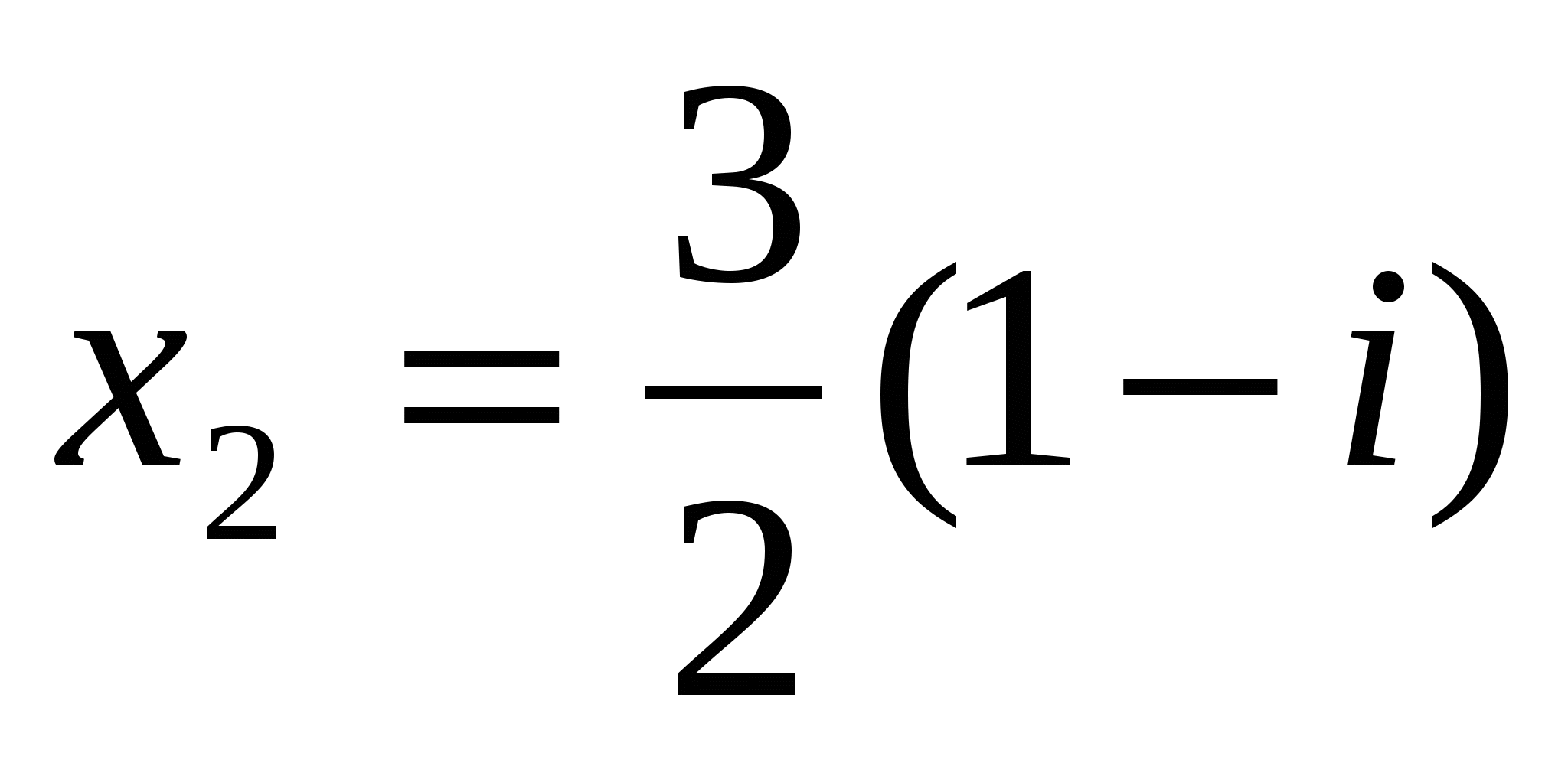

Итак, в множестве комплексных чисел любое квадратное уравнение имеет решение.

Возведение комплексного числа 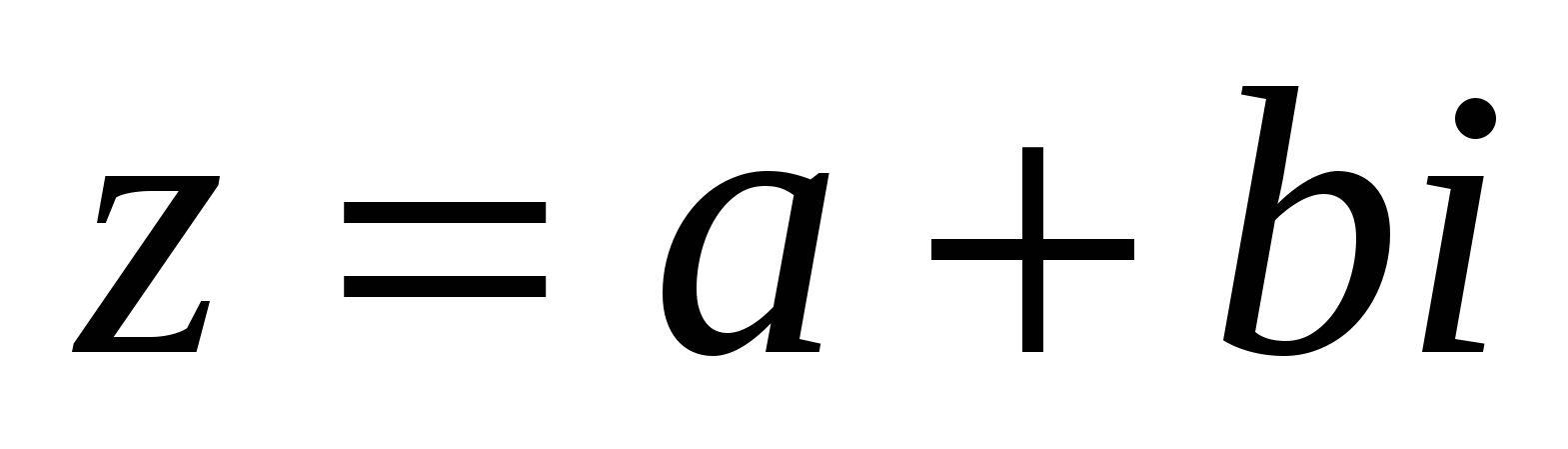в степень п (п N) рассматривается как частный случай умножения комплексных чисел:

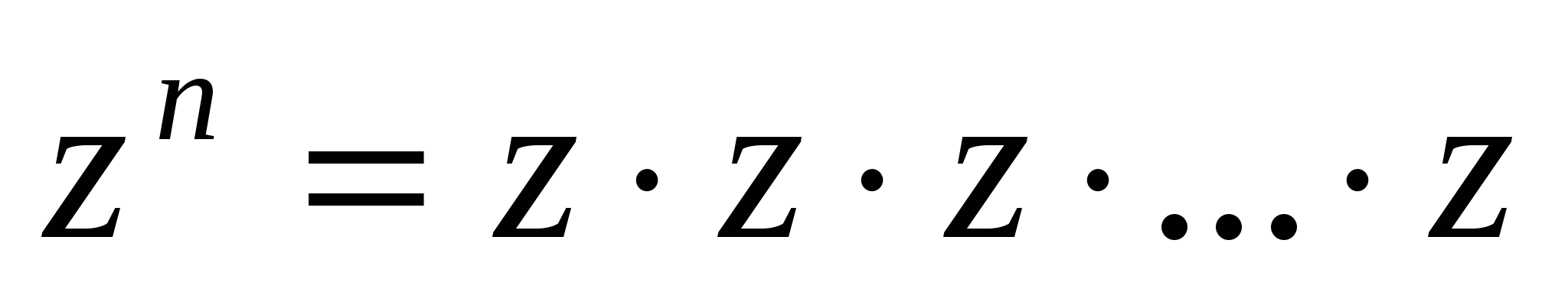(п раз) (7)

Найдем натуральные степени мнимой единицы i. На основании ра­венства (4) получаем:

,

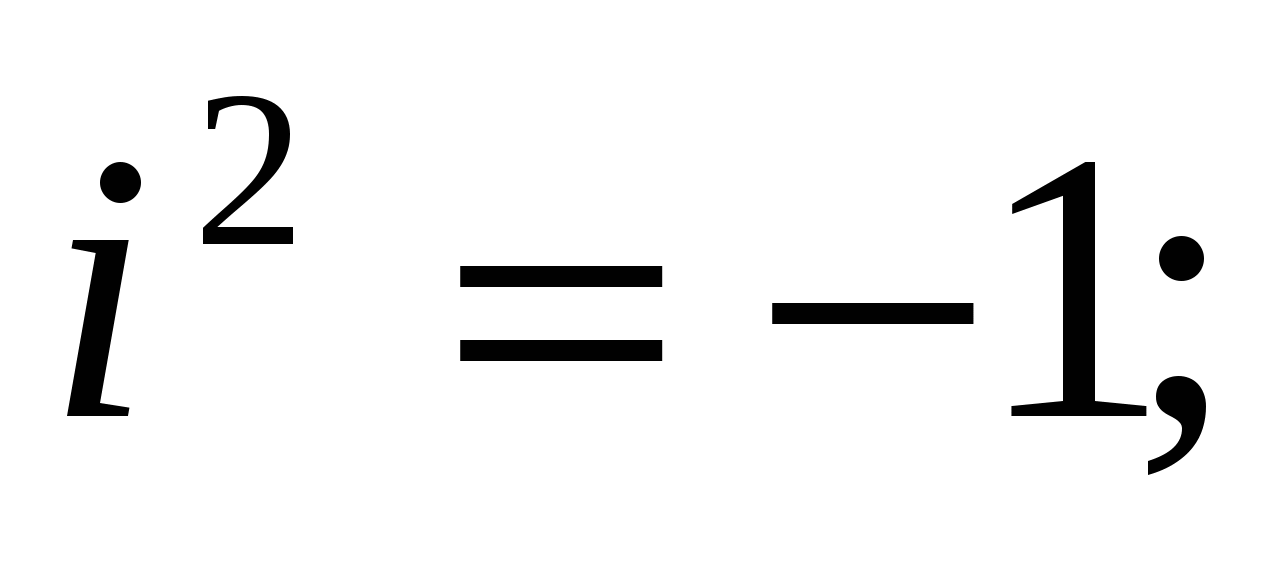
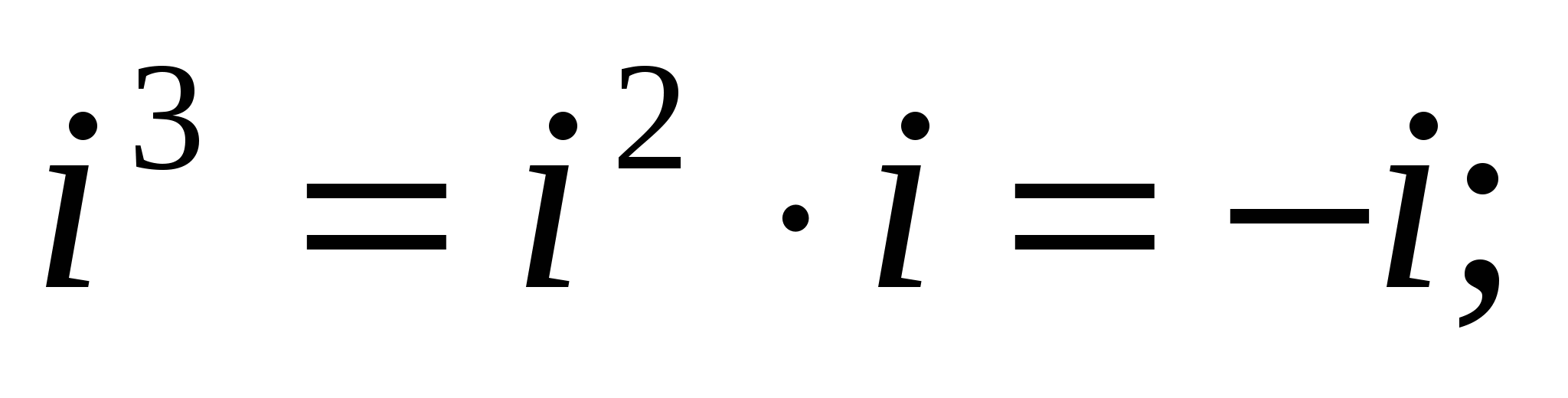
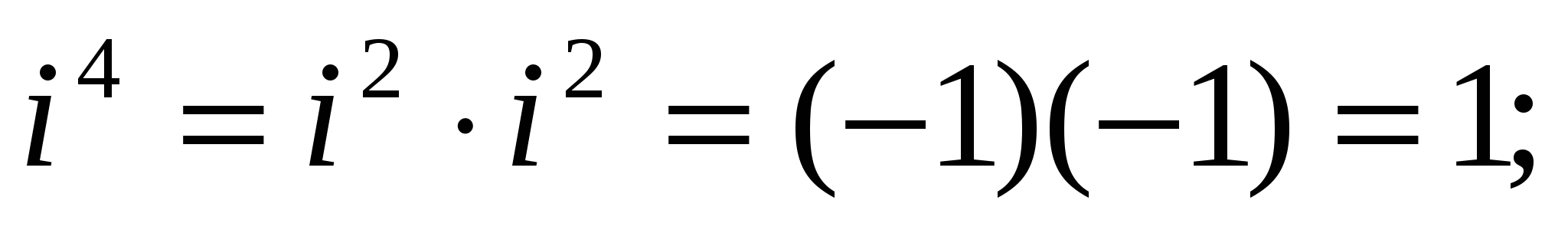
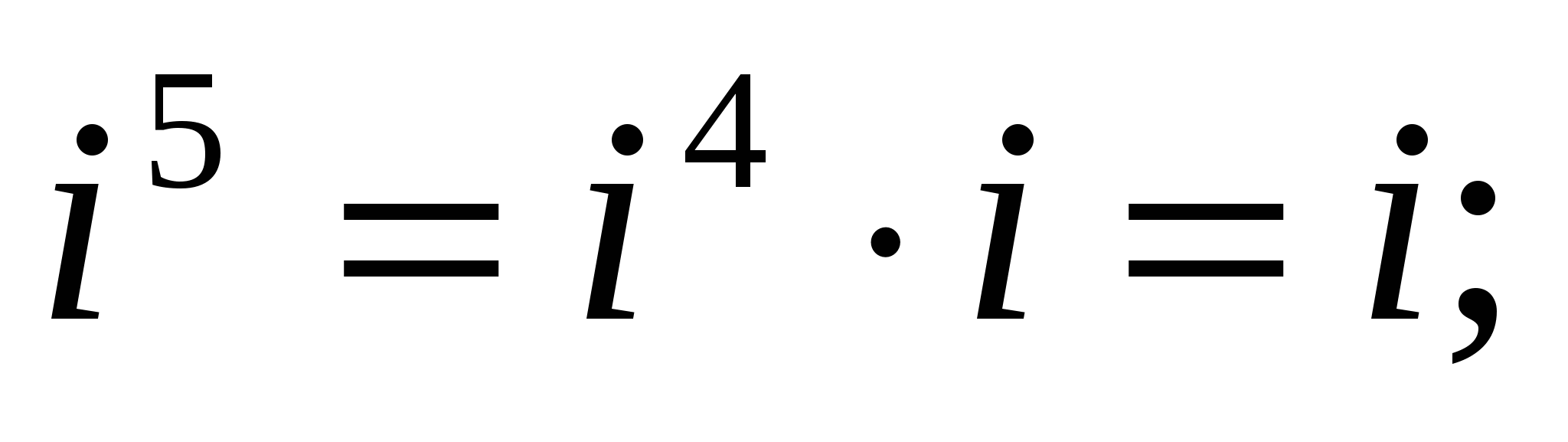
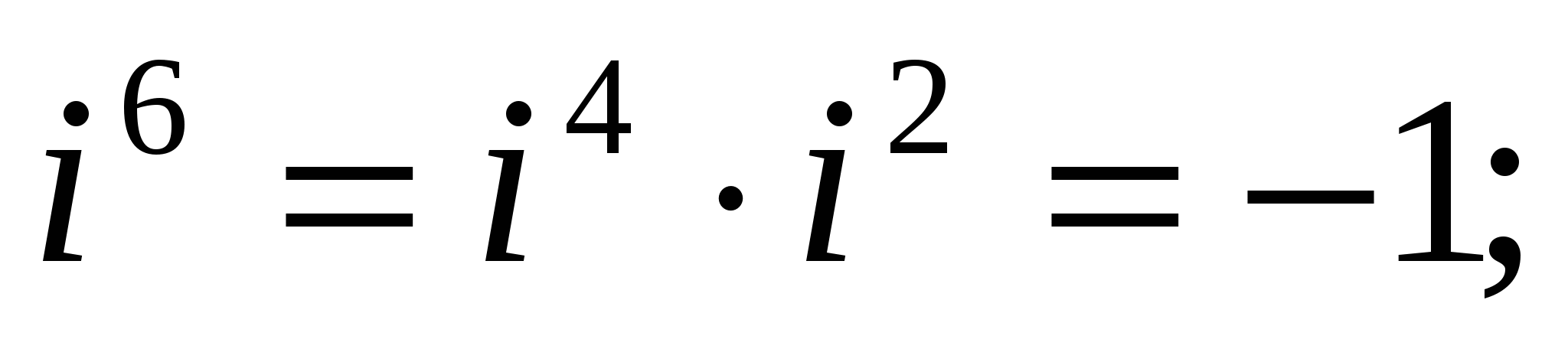
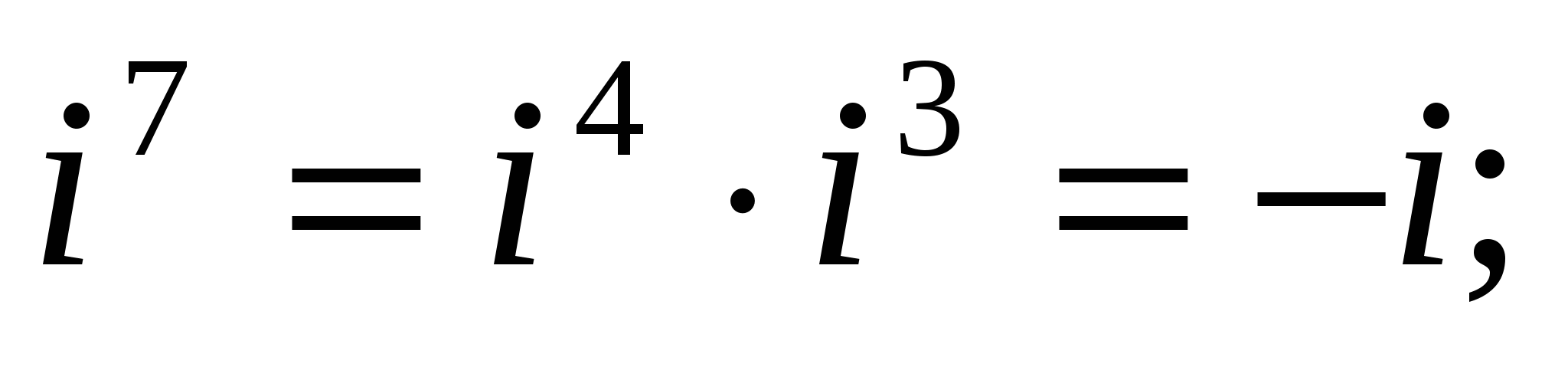
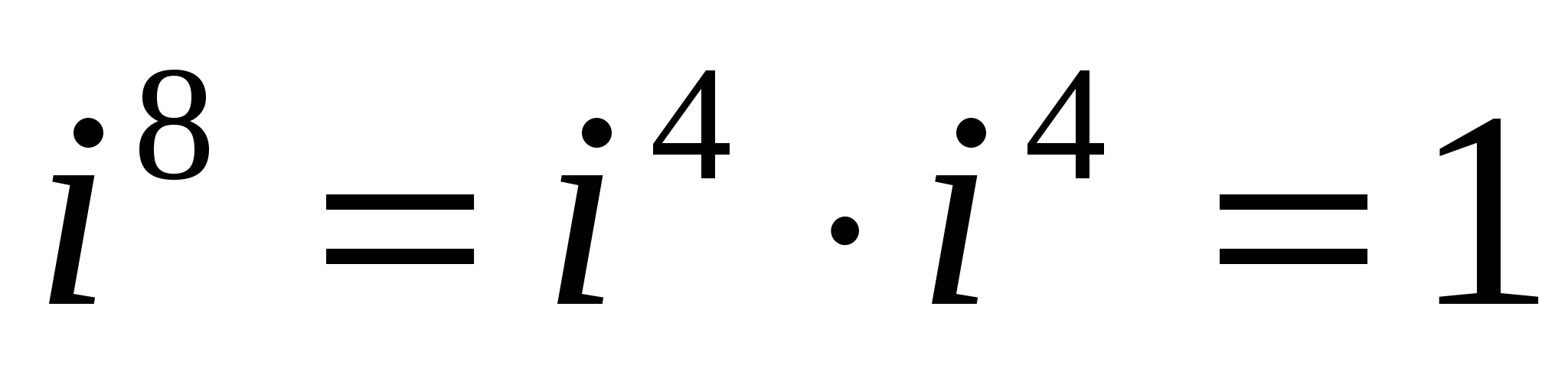и вообще

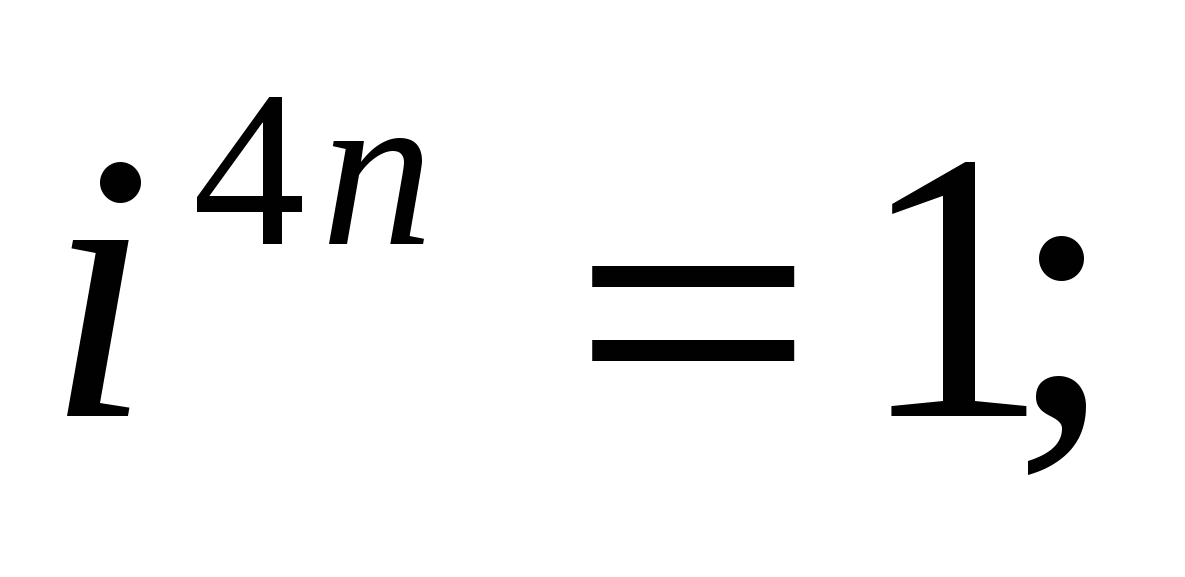
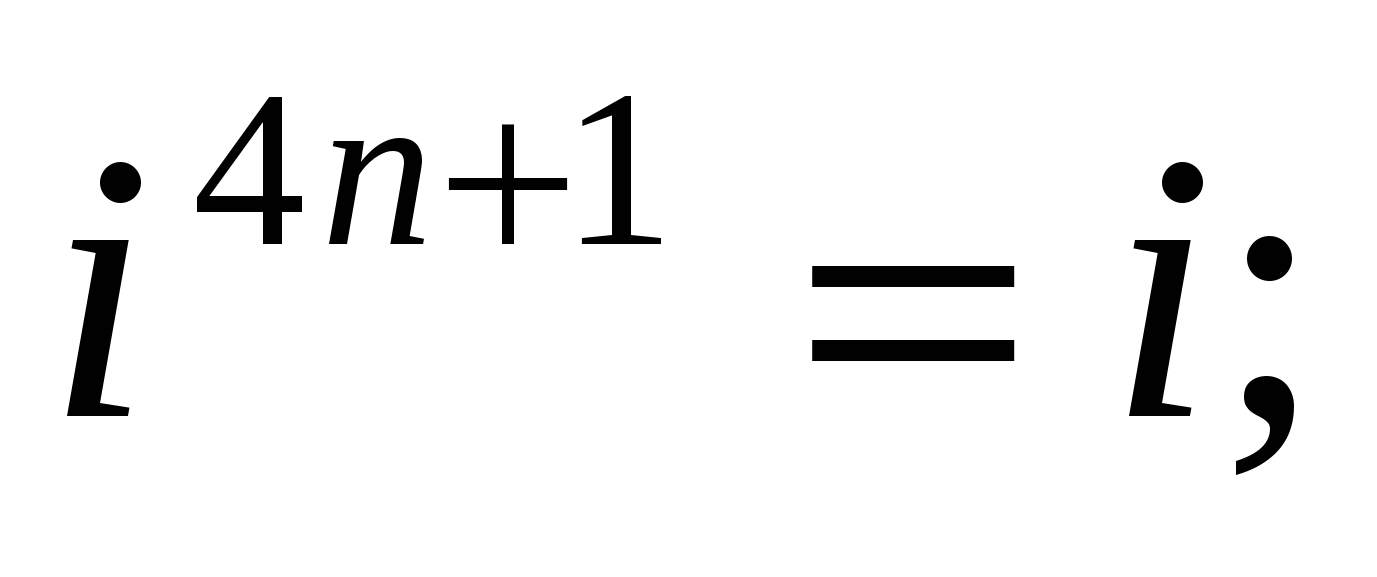
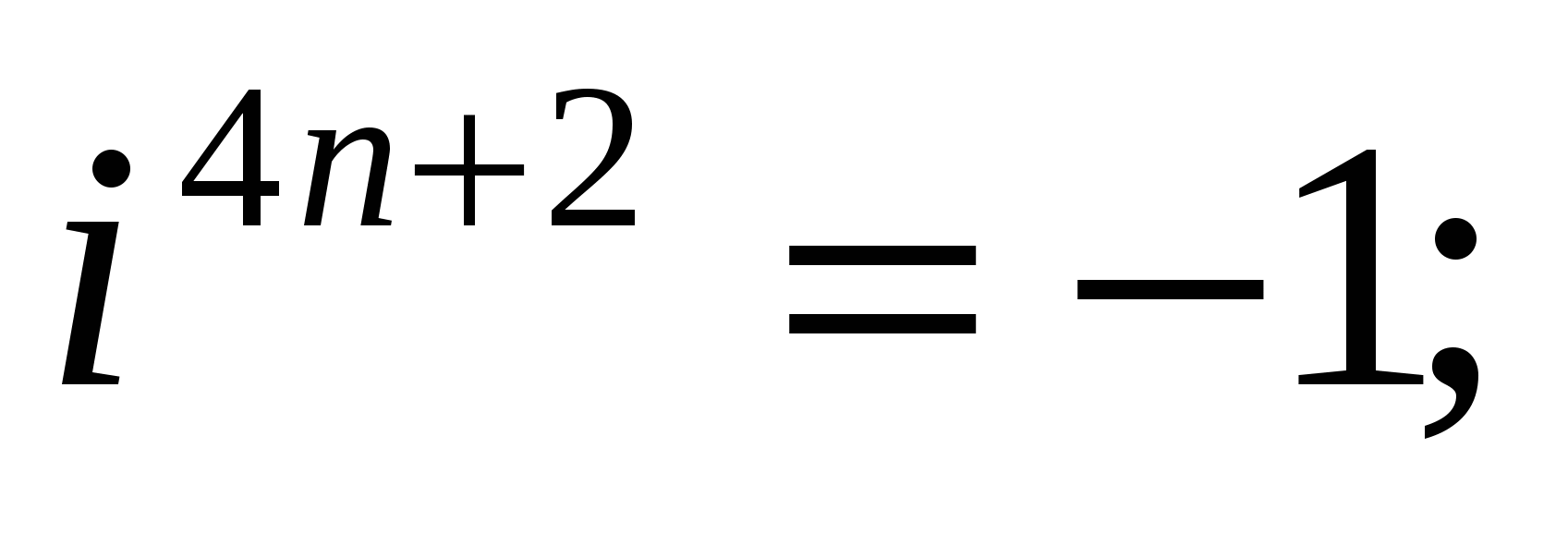
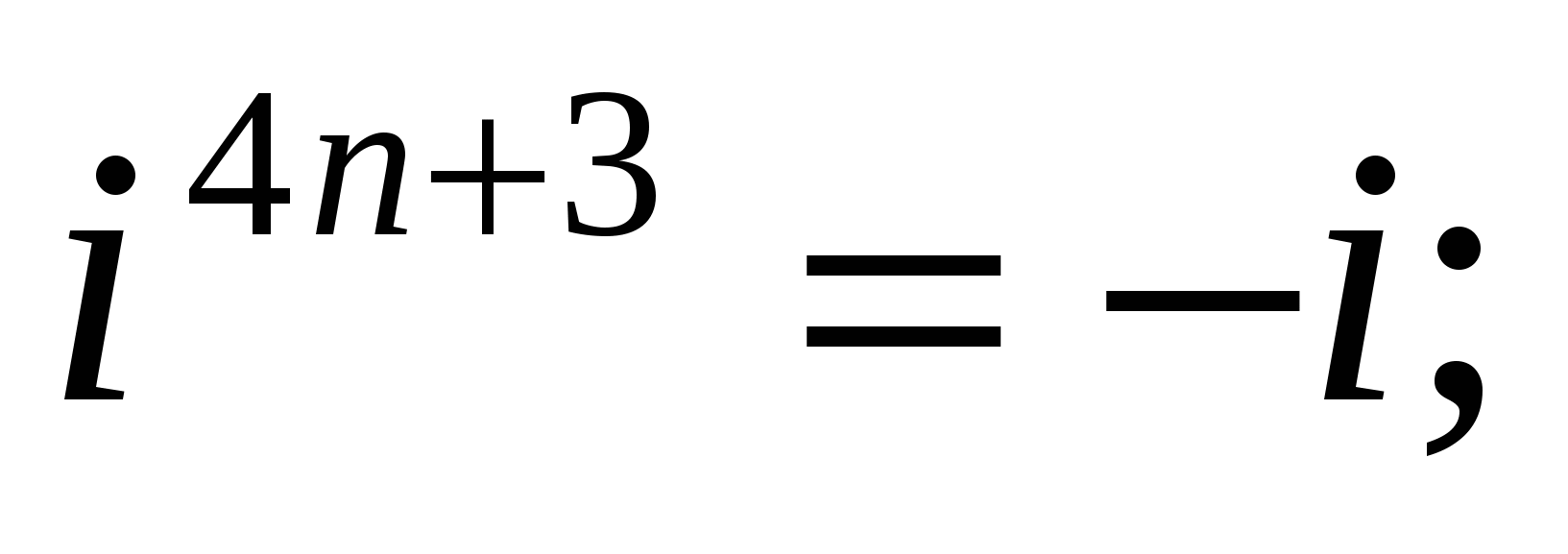
где п — любое натуральное число.

Пример2. Найти _.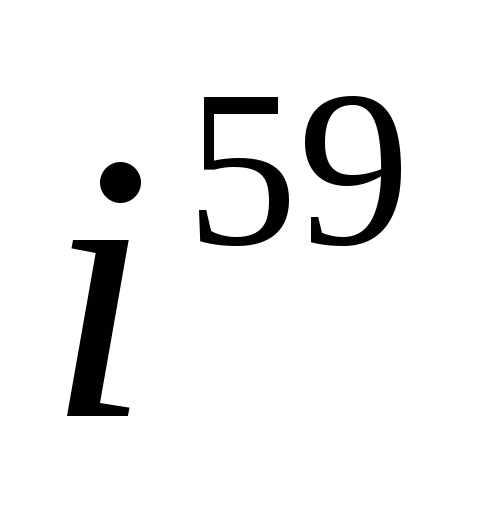

Решение. При делении числа 59 на 4 имеем: 59 = 14 • 4 + 3, поэтому

.

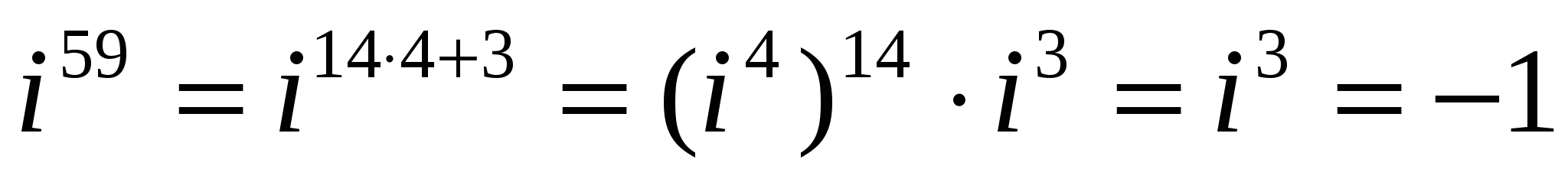Пример 3. Решить квадратные уравнения:

1) z² + 2 z + 5 = 0; 2) 4 z ² —2 z + 1= 0;

Решение.

1) z² + 2 z + 5 = 0; D = 4 − 4∙ 5 = 4 – 20 = -16; 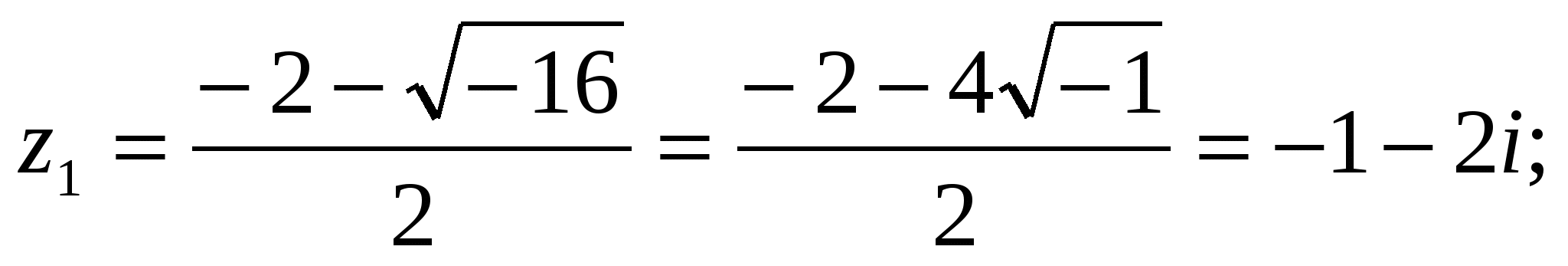z ₂ = −1 + 2 i.

2) 4 z ² − 2 z + 1= 0; D = 4 − 4∙ 4∙ 1 = 4 – 16 = -12;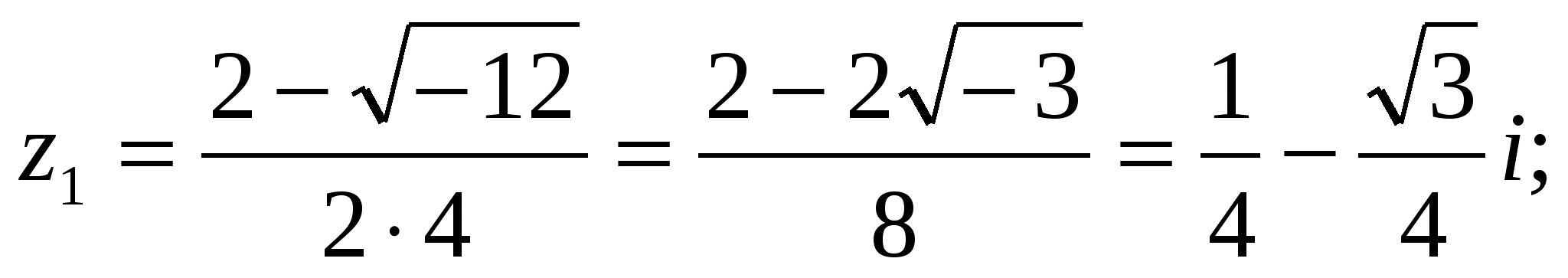

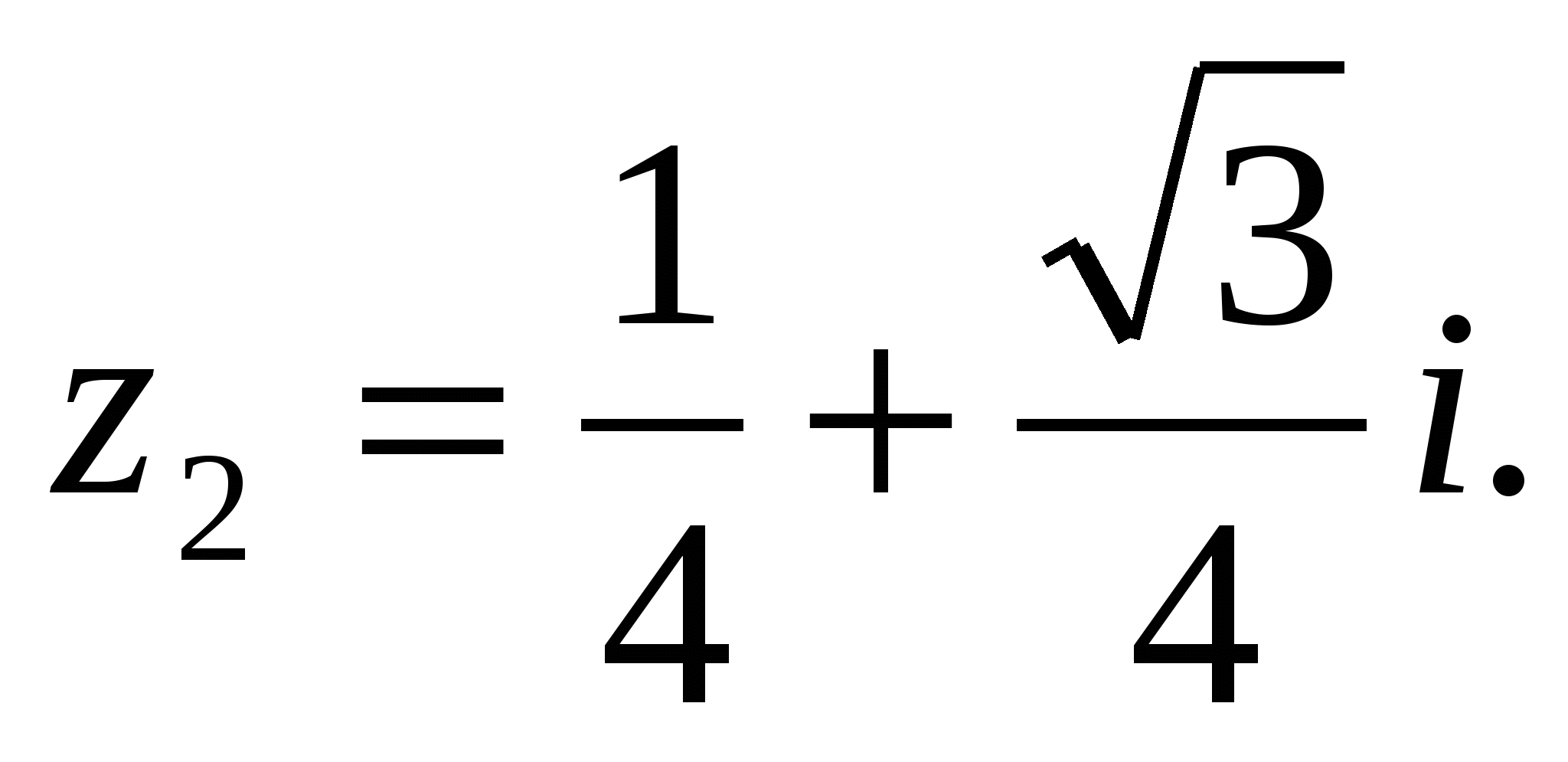
Ответ. 1) −1 ± 2 i; 2)

­