Построение аддитивной модели временного ряда

Тема 4. Временные ряды

Построение моделей временных рядов рассмотрим на примере. Пусть имеются некоторые условные данные об общем объеме потребления электроэнергии на одном из предприятий города.

Таблица 3.1

Год	Квартал	t	Объем потребления электроэнергии, , кВт
	I
II
III
IV
	I
II
III
IV
	I
II
III
IV
	I
II
III
IV

Построение аддитивной модели временного ряда

Обратимся к данным, представленным в табл. 3.1.

Данный временной ряд содержит сезонные колебания периодичностью 4, т.к. объем потребления электроэнергии в первый-второй кварталы ниже, чем в третий-четвертый. Рассчитаем компоненты аддитивной модели временного ряда.

Шаг 1. Проведем выравнивание исходных уровней ряда методом скользящей средней. Для этого:

1.1. Просуммируем уровни ряда последовательно за каждые четыре квартала со сдвигом на один момент времени и определим условные годовые объемы потребления электроэнергии (гр. 3 табл. 3.2).

1.2. Разделив полученные суммы на 4, найдем скользящие средние (гр. 4 табл. 3.2). Полученные таким образом выровненные значения уже не содержат сезонной компоненты.

1.3. Приведем эти значения в соответствие с фактическими моментами времени, для чего найдем средние значения из двух последовательных скользящих средних – центрированные скользящие средние (гр. 5 табл. 3.2).

Таблица 3.2

№ квар- тала, t	Объем потреб- ления электроэнергии,	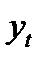Итого за четыре квартала	Скользящая средняя за четыре квартала	Центрированная скользящая средняя	Оценка сезонной компоненты
		–	–	–	–
			657,5	–	–
				655,25	213,75
				665,5	349,5
			708,75	693,75	‑336,75
				709,375	‑238,375
			718,25	714,125	277,875
			689,25	703,75	316,25
			689,25	689,25	‑299,25
			660,5	674,875	‑319,875
			678,25	669,375	322,625
				690,625	214,375
					‑233
			690,5	687,75	‑233,75
		–	–	–	–
		–	–	–	–

Шаг 2. Найдем оценки сезонной компоненты как разность между фактическими уровнями ряда и центрированными скользящими средними (гр. 6 табл. 3.2). Используем эти оценки для расчета значений сезонной компоненты (табл. 3.3). Для этого найдем средние за каждый квартал (по всем годам) оценки сезонной компоненты . В моделях с сезонной компонентой обычно предполагается, что сезонные воздействия за период взаимопогашаются. В аддитивной модели это выражается в том, что сумма значений сезонной компоненты по всем кварталам должна быть равна нулю.

Таблица 3.3

Показатели	Год	№ квартала, i
I	II	III	IV
	–	–	213,75	349,5
	‑336,75	‑238,375	277,875	316,25
	‑299,25	‑319,875	322,625	214,375
	‑233	‑233,75	–	–
Всего за i ‑й квартал		‑869	‑792	814,25	880,125
Средняя оценка сезонной компоненты для i ‑го квартала,		‑289,667	‑264	271,417	293,375
Скорректированная сезонная компонента,		‑292,448	‑266,781	268,636	290,593

Для данной модели имеем:

.

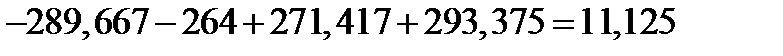Корректирующий коэффициент: .

Рассчитываем скорректированные значения сезонной компоненты
() и заносим полученные данные в таблицу 3.3.

Проверим равенство нулю суммы значений сезонной компоненты:

.

Шаг 3. Исключим влияние сезонной компоненты, вычитая ее значение из каждого уровня исходного временного ряда. Получим величины (гр. 4 табл. 3.4). Эти значения рассчитываются за каждый момент времени и содержат только тенденцию и случайную компоненту.

Шаг 4. Определим компоненту T данной модели. Для этого проведем аналитическое выравнивание ряда () с помощью линейного тренда. Результаты аналитического выравнивания следующие:

.

Подставляя в это уравнение значения , найдем уровни T для каждого момента времени (гр. 5 табл. 3.4).

Шаг 5. Найдем значения уровней ряда, полученные по аддитивной модели. Для этого прибавим к уровням T значения сезонной компоненты для соответствующих кварталов (гр. 6 табл. 3.4).

На одном графике отложим фактические значения уровней временного ряда и теоретические, полученные по аддитивной модели.

Таблица 3.4

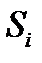
t				T
		‑292,448	667,448	672,700	380,252	‑5,252	27,584
		‑266,781	637,781	673,624	406,843	‑35,843	1284,721
		268,636	600,364	674,547	943,183	‑74,183	5503,117
		290,593	724,407	675,470	966,063	48,937	2394,830
		‑292,448	649,448	676,394	383,946	‑26,946	726,087
		‑266,781	737,781	677,317	410,536	60,464	3655,895
		268,636	723,364	678,240	946,876	45,124	2036,175
		290,593	729,407	679,163	969,756	50,244	2524,460
		‑292,448	682,448	680,087	387,639	2,361	5,574
		‑266,781	621,781	681,010	414,229	‑59,229	3508,074
		268,636	723,364	681,933	950,569	41,431	1716,528
		290,593	614,407	682,857	973,450	‑68,450	4685,403
		‑292,448	753,448	683,780	391,332	69,668	4853,630
		‑266,781	720,781	684,703	417,922	36,078	1301,622
		268,636	651,364	685,627	954,263	‑34,263	1173,953
		290,593	636,407	686,550	977,143	‑50,143	2514,320

Рис. 3.4.

Для оценки качества построенной модели применим сумму квадратов полученных абсолютных ошибок.

.

Следовательно, можно сказать, что аддитивная модель объясняет 97% общей вариации уровней временного ряда по кварталам за 4 года.

Шаг 6. Прогнозирование по аддитивной модели. Предположим, что по нашему примеру необходимо дать прогноз об общем объеме потребления электроэнергии на I и II кварталы 2003 года. Прогнозное значение уровня временного ряда в аддитивной модели есть сумма трендовой и сезонной компонент. Для определения трендовой компоненты воспользуемся уравнением тренда

.

Получим

;

.

Значения сезонных компонент за соответствующие кварталы равны: и . Таким образом,

;

.

Т.е. в первые два квартала 2003 г. следовало ожидать объема потребления электроэнергии порядка 395 и 422 кВт соответственно.