Особенности задач линейного программирования, на которых основаны методы решения ЗЛП, можно проиллюстрировать с помощью графической интерпретации. Это возможно, когда вектор X содержит две переменные. Рассмотрим графическую интерпретацию ЗЛП на следующем примере.
Пример. Дана следующая задача линейного программирования:
3 x 1 2 х 2 → max,
2 х 1 + 4 х 2 ≤ 16,
x 1 ≤ 6,
x 2 ≤ 8, х 1, х 2 ≥ 0.
Для графической интерпретации задачи построим систему координат x 1O x 2 (рис. 7). Любая точка в этой системе задается своими координатами на осях О х 1 и О х 2 – (х 1, х 2), т. е. так же, как и вектор X. Таким образом, решени- ем задачи будет некоторая точка в пространстве X 1O х 2.
Если учитывать требование неотрицательности переменных и не учиты-
вать другие ограничения ЗЛП, то решением задачи может быть любая точка из той части плоскости, которая расположена выше и левее осей O х 1 и О х 2. Определим в этой части плоскости область допустимых решений данной за- дачи (говорят также – область допустимых значений переменных вектора X). Для этого нарисуем прямые, заданные уравнениями 2 х 1 + 4 х 2 = 16, х 1 = 6, х 2 = 8 (см. рис. 7). Относительно ограничения х 1 ≤ 6 допустимыми будут те реше- ния (точки), которые лежат левее прямой х 1 = 6 или на ней, относительно ограничения x 2 ≤ 8 – те решения, которые лежат ниже прямой х 2 = 8 или на ней. Относительно ограничения 2 х 1 + 4 х 2 ≤ 16 допустимыми будут те реше- ния, которые лежат левее или на прямой 2 х 1 + 4 х 2 = 16. Область допустимых решений задачи есть та область в х 1О х 2, точки которой удовлетворяют всем этим ограничениям, включая требования неотрицательности. Такой областью на рис. 7 является область OABD, которая есть пересечение перечисленных областей, и решением заданной ЗЛП является точка этой области. Решим эту задачу графическим методом, т. е. по рисунку.
|
|
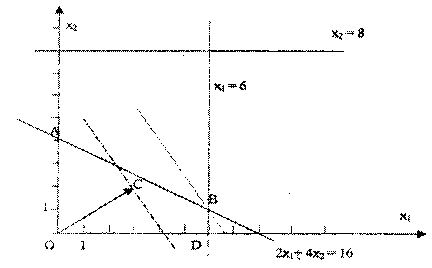
Рис. 7. Система координат для графической интерпретации задачи линейного программирования при поиске области допустимых значений
Алгоритм решения следующий.
Шаг 1. Построить графическую интерпретацию ЗЛП, определить и ука-
зать на рисунке область допустимых решений.
Шаг 2. Построить вектор ОС с координатами (c 1, с 2). Здесь с 1, с 2 – коэф- фициенты при переменных в выражении целевой функции. В нашем примере это вектор ОС = (3, 2), который изображен на рис. 7.
Шаг 3. Провести линию, перпендикулярную вектору ОС. Это есть линия уровня целевой функции (на рис. 7 она показана штрихпунктиром).
Шаг 4. Для поиска оптимального решения перемещать линию уровня по направлению вектора ОС при поиске максимума, или против направления вектора ОС – при поиске минимума. Линию перемещать до тех пор, пока она не достигнет последней точки области допустимых решений. Эта точка и будет оптимальным решением задачи (на рис. 7 оптимальное решение – точка В).
Примечание. Линию уровня следует перемещать изнутри области допусти- мых решений к ее краю. В нашем примере это замечание неактуально, однако в других задачах может получиться так, что, рисуя перпендикуляр вектору ОС в конце вектора, мы получим линию вне области допустимых решений. В этом слу- чае ее необходимо переместить внутрь области, а потом уже осуществлять по- иск оптимума.
Шаг 5. Определить координаты оптимального решения. Это делается или по рисунку, или путем решения системы уравнений тех прямых, на пересече- нии которых лежит точка оптимального решения. В нашем примере это была
|
|
бы система уравнений:
2 х 1 + 4 х 2= 16,
х 1 = 6.
Для данной задачи решением будет точка В с координатами (6, 1). Иначе говоря, решением задачи являются значения переменных х 1 = 6, х 2 = 1. Под- ставляя эти значения в выражение для целевой функции, можно определить оптимальное значение критерия, в нашем случае I = f (X opt) = 27. Если бы в нашем примере необходимо было найти минимум целевой функции, то ре- шением была точка (0, 0).
На основе анализа примера можно сформулировать следующие особенно-
сти ЗЛП:
– область допустимых решений задачи линейного программирования ограничена прямыми линиями, т. е. является многогранником;
– решение ЗЛП, если оно является единственным, лежит на одной из вершин многогранника (точка В в примере). Если решений множество, то они лежат на грани многогранника (это могло бы получиться, если бы в при- мере вектор ОС оказался перпендикулярным прямой 2 х 1 + 4 х 2 = 16, тогда бы- ло бы бесконечное множество решений – точек на отрезке АВ);
– в ЗЛП может и не существовать решений, если область допустимых решений не замкнута. Так, если в примере убрать ограничения 2 х 1 + 4 х 2 ≤ 16 и х 2 ≤ 8, и убрать соответствующие прямые на рис. 7, то двигать линию уров- ня можно было бы до бесконечности, т. е. решение бы отсутствовало.
На этих особенностях основан наиболее известный метод решения ЗЛП – симплекс-метод. Сущность его сводится к следующему: по определенным пра- вилам при решении задачи ищутся так называемые базисные решения (сим- плексы). Эти базисные решения совпадают с вершинами многогранника обла- сти допустимых решений (на рис. 7 это точки О, А, В, D). В процессе поиска ба- зисных решений оценивается их оптимальность по правилам, позволяющим определить, можно ли улучшить значение целевой функции, если выбрать ка- кое-то другое базисное решение. Если можно – выбирается новое базисное ре- шение (новая вершина многогранника) и проверка повторяется. Это делается до тех пор, пока найденное базисное решение не окажется оптимальным.
|
|