Рассмотренный графический метод очень прост, нагляден и быстро приводит к решению задачи ЛП. Но он позволяет решать только такие задачи, в которых всего две независимые переменные, тогда как задачи, возникающие на практике обычно имеют значительно большее число переменных.
Существуют методы ЛП, позволяющие решать задачи с любым числом переменных, причем с использованием обычных арифметических вычислений. Несмотря на отдельные различия в этих методах, всех их объединяет общий принцип нахождения оптимума задачи – это принцип последовательного приближения.
Вначале из числа возможных вариантов выделяется какой-либо один вариант, который в общем случае не является оптимальным. Затем, путем определенных вычислительных приемов, производится его последовательное улучшение. В результате всякий раз получают новые варианты, все более близкие к оптимальному. Процесс продрлжается до тех пор, пока не будет получен вариант, который уже нельзя улучшить. Этот вариант и будет оптимальным.
Наиболее универсальным методом данного класса является так называемый симплексный метод. Суть его заключается в следующем.
Рассмотрим обощенную задачу ЛП с функциональными ограничениями в форме равенств:
(4-28)
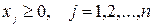
Заметим, что в данном случае оптимум задачи отыскивается в виде точки минимума целевой функции, что, однако, не является принципиальным, так как минимуму функции соответствует максимум этой же функции, взятой с противоположным знаком. Что касается формы задания функциональных ограничений, то, как уже отмечалось выше, линейные неравенства достаточно просто преобразуются в уравнения и обратно. Таким образом, приведенная задача в целом соответствует раннее рассмотренной обощенной постановке задачи ЛП.
|
|
Пусть в функциональных ограничениях задачи значения правых частей неотрицательны, т.е. bi ≥ 0, i=1,2,…,m. Рассмотрим эти ограничения, как систему линейных алгебраических уравнений. Из теории известно, что если ранг матрицы коэффициентов данной системы равен r, причем r<m, r<n, она может быть однозначно разрешена относительно r переменных, т.е. r переменных системы выразить через (n-r) остальных переменных. Следовательно, система может быть приведена к виду:
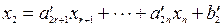
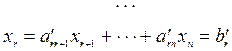(4-29)
где верхний штрих в обозначениях указывает на модифицированное значение коэффициентов при переменных и свободных членов в уравнениях.
Переменные 
в левой части уравнений называются базисными, а весь их набор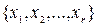 
- базисом. Остальные переменные называются небазисными или свободными.
Подставляя в выражение целевой функции (4-28) вместо базисных переменных их выражения через небазисные, получим зависимость целевой функции от небазисных переменных:
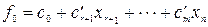(4-30)
Положим, что все небазисные переменные равны нулю, т.е.
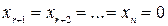(4-31)
Тогда из системы (4-29) можно получить следующие значения базисных переменных:
(4-32)
Совместно с (4-31) данные значения базисных переменных, с учетом неотрицательности значений bi, i=1,2,…,m, образуют допустимое решение системы
(
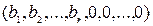(4-33)
Данное решение будет называться базисным, соответствующим базису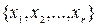 
.
С учетом (4-30), для всякого базисного решения имеет место:
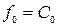(4-34)
При этом можно показать, что любому базисному решению соответствует вершина многогранника ОДР в пространстве базисных переменных. Справедливо и обратное утверждение: любой вершине ОДР в пространстве базисных переменных соответствует базисное решение. На этом свойстве базисных решений основан симлекс-метод линейного программирования.
|
|
Проследим идею симлекс-метода на примере. Пусть система функциональных ограничений задачи ЛП задана в виде:
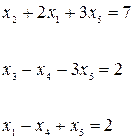(4-35)
Целевая функция задачи:
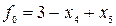(4-36)
Нетрудно убедиться, что система (4-35) совместна, а ее ранг r=3. Таким образом, число свободных переменных k=5-3=2.
Выберем в качестве свободных переменных х4 и х5. Тогда в базис системы войдут переменные х1,х2,х3. С учетом этого получим:
(4-37)
Целевая функция (3-33) не нуждается в преобразовании, так как уже выражена через свободные переменные.
Чтобы получить базисное решение, положим свободные переменные, равными нулю, т.е. х4 = х5 =0. Тогда из (4-37) базисные переменные определятся следующим образом:
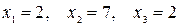(4-38)
Полученные значения положительны, следовательно допустимы. Отсюда, набор значений
(4-39)
образует допустимое базисное решение системы (4-35), при этом 
.
Проверим, является ли это решение оптимальным? Поскольку х4 входит в выражение целевой функции (4-36) с отрицательным коэффициентом, можно попытаться улучшить (уменьшить) значение 
путем увеличения положительного значения данной переменной, сохраняя неизменным нулевое значение для другой свободной переменной х5. Однако, это следует делать так, чтобы при изменении значения х4 значения базисных переменных х1,х2,х3 не стали отрицательными.
|
|
Из первого уравнения системы (4-37) следует, что, если х4 станет больше 2, то переменная х1 станет отрицательной. В то же время, при увеличении х4 до 2 переменная х3 увеличивает свое положительное значение, а переменная х2, хотя и уменьшается, все же остается положительной. Следовательно переменной х2 можно придать значение 2. При этом получим новое базисное решение:
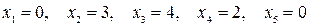, (4-40)
для которого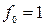 
. Новый базис включает переменные х2,х3,х4.
Чтобы соответствующим образом преобразовать систему ограничений задачи, выразим новые базисные переменные х2,х3,х4 через новые свободные переменные х1 и х5. Из первого уравнения системы (3-24) получим:
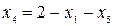(4-41)
С учетом этого выражения получим преобразованную систему ограничений и целевую функцию:
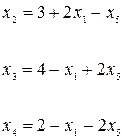(4-42)
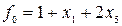(4-43)
Проведем теперь аналогичное исследование для целевой функции (4-43). Здесь всякое увеличение любой переменной 
приводит только к увеличению значения 
. Поэтому найденное раннее решение (4-40) и соответствующее ему значение 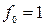являются оптимальными.
Приведенный пример показывает, что оптимум задачи ЛП может быть найден путем последовательного перехода от одного базисного решения системы уравнений в функциональных ограничениях задачи к другому базисному решению. Однако, каждый такой переход совершается не произвольно, а обеспечивая улучшение значения целевой функции. В этом и сотоит основное содержание симплекс-метода ЛП.
В геометрической интерпритации симплекс-метод ЛП заключается в последовательном переходе из одной вершины пространственного многогранника ОДР в эту же вершину или другую смежную вершину, руководствуясь правилом улучшения значения целевой функции. При этом начало поиска может выполняться из любой вершины многогранника. Смежной (соседней) вершиной считается такая, которая имеет общую грань с текущей вершиной.