Прямая на плоскости. Кривые второго порядка

1. Уравнение прямой на плоскости.

2. Взаимное расположение двух прямых на плоскости.

3. Уравнение прямой в нормальной форме. Расстояние от точки до прямой.

4. Кривые второго порядка.

1.

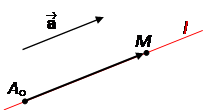Прямую l на плоскости можно задать

а) с помощью точки A _oÎ l и ненулевого вектора ½½ l ;

б) с помощью точки A _oÎ l и ненулевого вектора ^ l;

 

в) с помощью двух точек A _o, A ₁Î l.

 

Вектор ½½ l называется направляющим вектором прямой, а вектор ^ l называется вектором нормали к прямой.

Теорема 1. 1. Прямая l, проходящая через точку A _o(x _o, y _o), и имеющая направляющий вектор (a ₁, a ₂), задается уравнением

=, (1)

которое называется каноническим уравнением прямой, или параметрическими уравнениями:

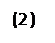
x = x _o + a ₁ t,

y = y _o + a ₂ t, t Î R,

которые можно записать в векторном виде так:

= + t, t Î R, (2¢)

где = – радиус-вектор точки A _o.

2. Прямая, проходящая через две точки A _o(x _o, y _o) и A ₁(x ₁, y ₁), задается уравнением

=, (3)

3. Прямая, проходящая через точку A _o(x _o, y _o), и имеющая вектор нормали (A, B), задается в декартовой СК уравнением

A (x – x _o) + B (y – y _o) = 0. (4)

4. Прямая, отсекающая на координатных осях отрезки длины a ¹ 0, b ¹ 0, задается уравнением

+ = 1, (5)

(уравнение прямой в отрезках).

 

 

Доказательство. 1. Пусть M (x, y) – произвольная точка прямой l. Тогда (x – x _o, y – y _o)½½ (a ₁, a ₂), а по второму признаку коллинеарности векторов это равносильно (1).

Обратно, если для координат точки M (x, y) выполнено (1), то по тому же признаку ½½, а значит, M Î l.

По первому признаку коллинеарности векторов ½½ Û $ t Î R, такое что = t . В координатах последнее равенство имеет вид

x – x _o = t a ₁, y – y _o = t a ₂,

Для того, чтобы получить уравнение (2) осталось перенести x _o и y _o в другую часть равенства.

2. Если прямая проходит через две точки A _o(x _o, y _o) и A ₁(x ₁, y ₁), то вектор (x ₁– x _o, y ₁– y _o) можно взять в качестве направляющего вектора прямой. Подставляя его координаты в (1) вместо a ₁, a ₂, получим (3).

3. Пусть M (x, y) – произвольная точка прямой l. Тогда

(x – x _o, y – y _o) ^ (A, B) Û · = 0, а в координатах это условие как раз имеет вид (12). Обратно, если координаты точки M (x, y) удовлетворяют (4), то ^ , а значит, M Î l.

4. Условие означает, что прямая проходит через точки A (a, 0) и B (0, b). Подставляя их координаты в (2), получим

= Û = Û (5).

Следствие. Любая прямая на плоскости может быть задана уравнением вида

Ax + By + C = 0, (6)

которое называется общим уравнением прямой. И обратно, любое уравнение вида (14) на плоскости задает прямую.

Доказательство. Любую прямую на плоскости можно задать с помощью точки и вектора нормали. Тогда ее уравнение в декартовой СК будет иметь вид (12). Раскроем скобки:

Ax + By – Ax _o– By _o = 0

и обозначим C = – Ax _o– By _o= const. Получим уравнение (6).

Обратно, пусть некоторое множество l определяется уравнением (6), и A _o(x _o, y _o) – произвольная точка этого множества. Тогда ее координаты удовлетворяют (6): Ax _o + By _o + C = 0 Þ C = – Ax _o– By _o. Подставляя это значение в (6) получим (4), а это уравнение, как уже известно, определяет прямую.

Попутно мы выяснили геометрический смысл коэффициентов A и B в общем уравнении прямой: это координаты вектора нормали к прямой: (A, B). И этот факт чрезвычайно важен при исследовании положения прямой и при решении различных задач про прямую на плоскости. Но этот факт верен только в случае декартовой СК.

Если СК на плоскости не является декартовой, то это следствие можно доказать с помощью уравнения (1). В дальнейшем, СК предполагается декартовой, если не оговорено противное.

Рассмотрим различные частные случаи общего уравнения прямой.

1. C = 0 Û l : Ax + By = 0. Тогда урав-нению удовлетворяют координаты точки O (0, 0), т.е. прямая проходит через начало координат.

2. A = 0 Û By + C = 0 Û y = – C / B. Прямая l || Ox.

3. B = 0 Û Ax + C = 0 Û x = – C / A. Прямая l || Oy.

 

 

4. B ¹ 0. Тогда (6) можно переписать так: y = – x –. Обозначим k = – A/B, q = – C / B, и получим уравнение

y = k x + q, (7)

которое называется уравнением прямой с угловым коэффициентом. Угловым называется коэффициент k. Выясним почему.

Пусть P (x ₁, y ₁), Q (x ₂, y ₂) – две произвольные точки на прямой l, где y ₂ ³ y ₁. Подставим их координаты в уравнение прямой: y ₁ = k x ₁ + q, y ₂ = k x ₂ + q. Вычтем из второго равенства первое:

y ₂ – y ₁= k (x ₂ – x ₁).

Поскольку мы исключили случай l ½½ Oy, то x ₂ ¹ x ₁ Þ

k =. (***)

Выберем на прямой l направление, соответствующее возрастанию ординаты y, и назовем его положительным. Пусть a – угол между положительным направлением оси Ox и положительным направлением прямой l. Назовем его углом наклона прямой. Пусть S – точка с координатами (x ₂, y ₁).

 

 

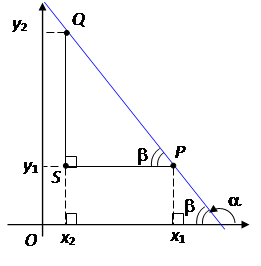1 случай: x ₂ > x ₁. Тогда y ₂ – y ₁ = QS, x ₂ – x ₁ = PS и из D PQS находим, что k = QS / PS = tg a.

2 случай: x ₂< x ₁. Тогда y ₂ – y ₁= QS, x ₂ – x ₁= – PS Þ k = – QS / PS = = – tg b, где b = Ð QPS. Но b = p – a Þ – tg b = tg a. Значит, как и в первом случае k = QS / PS = tg a.

Итак, мы доказали, что k есть тангенс угла наклона прямой. Поэтому он называется угловым коэффициентом. А геометрический смысл коэффициента q очевиден: это отрезок, отсекаемый прямой на оси Oy.

2.

Для удобства изложения будем считать, что совпадающие прямые – это частный случай параллельных.

Пусть две прямые на плоскости заданы общими уравнениями:

l ₁: A ₁ x + B ₁ y + C ₁ = 0 ,

l ₂: A ₂ x + B ₂ y + C ₂ = 0 .

Тогда мы сразу можем сделать вывод, что (A ₁, B ₁) и (A ₂, B ₂) – это векторы нормали к l ₁ и l ₂.

Теорема 2. 1. l ₁½½ l ₂ и l ₁¹ l ₂ Û = ¹.

2. l ₁= l ₂ Û = =.

3. l ₁^ l ₂ Û A ₁ A ₂ + B ₁ B ₂ = 0.

4. угол между l ₁ и l ₂ вычисляется по формуле

cos a = =. (8)

Доказательство. 1, 2. Очевидно, что l ₁½½ l ₂ Û ½½, а по второму признаку коллинеарности векторов это равносильно

= = l. (*)

При этом, прямые будут совпадать Û у них есть общая точка M _o(x _o, y _o), т. е. если одновременно выполняется

A ₁ x _o + B ₁ y _o + C ₁ = 0,

A ₂ x _o + B ₂ y _o + C ₂ = 0.

Вычтем из первого равенства второе, домноженное на l:

(A ₁– l A ₂) x _o + (B ₁– l B ₂) y _o + C ₁– l C ₂ = 0.

В силу (*) обе скобки равны нулю Þ C ₁– l C ₂ = 0 Û C ₁/ C ₂ = l. (**) Объединяя (*) и (**), получаем требуемый результат.

Обратно, если выполнено условие пункта 2, то уравнения прямых l ₁ и l ₂ пропорциональны, т.е., разделив первое уравнение на некоторое число l, мы получим второе уравнение. Значит эти уравнения равносильны и определяют на плоскости одно и то же множество.

3, 4. Напомним, что углом между двумя прямыми называется меньший из двух углов, которые образуются при их пересечении. Таким образом, угол a между прямыми находится в пределах 0 £ a £ p/2.

Пусть b =Ð(,). Тогда 0 £ b £ p.

Очевидно, что b совпадает с одним из двух углов, которые образуют прямые при пересечении.

1 случай: 0 £ b £ p/2. Тогда a = b Þ

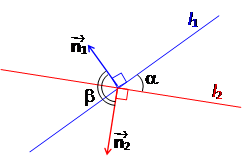cos a = cos b =.

2 случай: p/2 < b £ p. Тогда a = p – b и cos b < 0 Þ

cos a = cos (p – b) = – cos b =

=½ cos b½ = .

Эта формула подойдет и к первому

случаю: неотрицательную величину модулем не испортишь. Последнее равенство в (16) – эта та же формула, только расписанная в координатах. В частности, из (16) следует, что l ₁^ l ₂ Û · = 0 Û A ₁ A ₂ + B ₁ B ₂ = 0.

 

Теорема 3Пусть две прямые на плоскости заданы уравнениями с угловым коэффициентом

l ₁: y = k ₁ x + q ₁, l ₂: y = k ₂ x + q ₂.

Тогда угол между ними вычисляется по формуле

tg q =.

Доказательство. Пусть k ₁= tg a₁, k ₂ = tg a₂ , а q₁ и q₂ – углы, которые образуются при пересечении прямых (см. чертеж). Тогда q₁= b – a, и, если q₁£ p/2, то он будет считаться углом между l ₁и l ₂. В этом случае tg q₁³ 0.

Находим:

tg q₁= tg(b – a) = =.

Если q₁> p/2, то между прямыми считается q₂ = p – q₁. Тогда

tg q₂ = tg(p – q₁) = – tg q₁=½tg q₁½ =.

Эта формула подойдет и к первому случаю.

Заметим, что если убрать в числителе модуль, то получится формула, по которой можно вычислить ориентированный угол от l ₁ до l ₂, (отсчитываемый против часовой стрелки). Данный угол может находиться в пределах – p £ q £ p.

3.

Определение. Говорим, что общее уравнение прямой

Ax + By + C = 0, (6)

имеет нормальную форму, если A ²+ B ² = 1. Это равносильно тому, что вектор (A, B) – единичный.

Если уравнение (14) не имеет нормальной формы, то мы можем привести его к этой форме, разделив на:

x + y + = 0.

Тогда ²+ ²= 1.

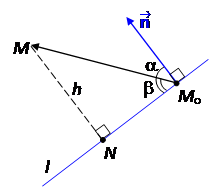
Теорема 4. Пусть прямая l определяется уравнением (6) в нормальной форме. Тогда расстояние от точки M (x ₁, y ₁) до прямой вычисляется по формуле

h =½ Ax ₁+ By ₁+ C ½. (9)

Следствие. Если прямая определяется произвольным уравнением вида (6), то

h = . (9¢)

Доказательство. Пусть (A, B) – вектор нормали к l. Поскольку уравнение имеет нормальную форму, то ½½ = 1. Пусть M _o(x _o, y _o) – произвольная точка на прямой. Опустим перпендикуляр MN

на прямую l . Пусть a =Ð( , ), b =Ð MM _o N .

1 случай. Точка M и вектор лежат в одной полуплоскости относительно прямой l. Тогда

h =½ MN ½=½ MM _o½·sin b =½½·sin( – a) =

=½½·cos a·½½= ·

(мы домножили на ½½, поскольку эта величина равна единице). Находим, что (x ₁– x _o, y ₁– y _o) Þ

h = A (x ₁– x _o) + B (y ₁– y _o) = Ax ₁+ By ₁+ C – (Ax _o+ By _o+ C)

(мы добавили и отняли C ). Поскольку M _oÎ l, то выражение в скобках равно нулю, и мы получаем

h = Ax ₁+ By ₁+ C.

2 случай. Точка M и вектор лежат в разных полуплоскостях относительно прямой l. Тогда b = a – p/2 Þ sin b = – cos a и те же самые вычисления дают

h = – · = – Ax ₁ – By ₁ – C.

Поскольку h – это расстояние, то h ³ 0. Это

значит, что во втором случае Ax ₁+ By ₁+ C < 0 (равенство исключается, т.к. M Ï l). Поэтому

h =½ Ax ₁+ By ₁+ C ½.

Эта формула подойдет и к первому случаю.

Попутно мы выяснили, что знак выражения Ax ₁+ By ₁+ C зависит от того, в какой полуплоскости находится точка M. Это позволяет для двух данных точек M ₁, M ₂ выяснить, лежат ли они в одной полуплоскости относительно прямой l или в разных (Û пересекает отрезок M ₁ M ₂ прямую l или нет).

4. Кривая второго порядка может быть задана уравнением:

Ах² + 2Bхy + Cy² + 2Dх + 2Ey + F = 0.

Существует система координат (не обязательно декартова прямоугольная), в которой данное уравнение может быть представлено в одном из видов, приведенных ниже.

Окружность

В окружности (х - а)² - (y - b)² = R² центр имеет координаты (a; b).

Эллипс

Эллипсом называется геометрическое место точек плоскости, для которых сумма расстояний до двух фиксированных точек плоскости, называемых фокусами эллипса, есть величина постоянная.

Отрезки, соединяющие точку эллипса с фокусами, называются фокальными радиусами точки.

Эллипс описывается каноническим уравнением:

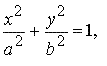
где a > 0, b > 0, a > b > 0 — большая и малая полуоси эллипса, то фокусы эллипса расположены симметрично на оси абсцисс и имеют координаты (−c, 0) и (c, 0), где

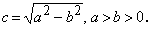
Величина e = c/a называется эксцентриситетом эллипса.

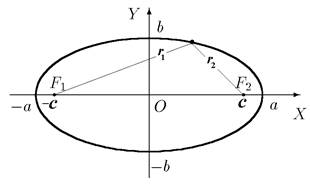
По определению эллипса r₁ + r₂ = 2a, r₁ и r₂ − фокальные радиусы, их длины вычисляются по формулам:

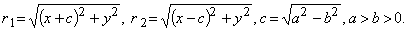
Гипербола

Гиперболой называется кривая второго порядка, которая в некоторой декартовой системе координат описывается уравнением:

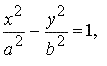
где a > 0, b > 0 — параметры гиперболы.

Это уравнение называется каноническим уравнением гиперболы, а система координат, в которой гипербола описывается каноническим уравнением, называется канонической.

В канонической системе оси координат являются осями симметрии гиперболы, а начало координат — ее центром симметрии.

Точки пересечения гиперболы с осью OX (± a, 0) называются вершинами гиперболы.

С осью OY гипербола не пересекается.

Отрезки a и b называются полуосями гиперболы.

Рис.1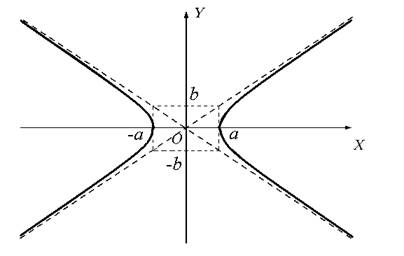

Прямые ay − bx = 0 и ay + bx = 0 — асимптоты гиперболы, при удалении точки гиперблы в бесконечность, соответствующая ветвь гиперболы приближается к одной из асимптот.

Уравнение описывает гиперболу, вершины которой лежат на оси OY в точках (0, ± b):

.

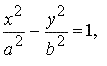
Рис.2

Такая гипербола называется сопряженной к гиперболе её асимптоты — те прямые ay − bx = 0 и ay + bx = 0. Говорят о паре сопряжённых гипербол.

Парабола

Параболой называется геометрическое место точек плоскости, для каждой из которых расстояние до фиксированной точки этой плоскости, называемой фокусом, равно расстоянию до фиксированной прямой, лежащей в той же плоскости и называемой директрисой параболы.

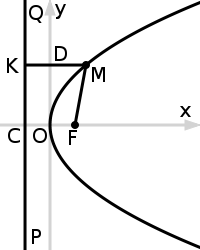
Каноническое уравнение параболы в прямоугольной системе координат:

(или 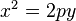, если поменять местами оси).

Число p называется фокальным параметром, оно равно расстоянию от фокуса до директрисы. Поскольку каждая точка параболы равноудалена от фокуса и директрисы, то и вершина — тоже, поэтому она лежит между фокусом и директрисой на расстоянии 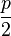от обоих.

Уравнение директрисы PQ: 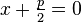, фокус F имеет координаты 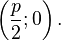Таким образом, начало координат O — середина отрезка CF.