Дом Учителя Уральского федерального округа
X Международная Олимпиада по основам наук
Третий этап. «Высшая лига»
Научный руководитель проекта по предмету: Мельников Юрий Борисович, доцент,
кандидат физико-математических наук, заведующий кафедрой Прикладной математики
Уральского государственного экономического университета, г. Екатеринбург.
Автор заданий: Унегова Татьяна Александровна, кандидат физико-математических наук, доцент кафедры высшей математики Уральского государственного педагогического университета, г. Екатеринбург.
Рецензент: Трубаева Наталия Валерьевна, учитель математики высшей квалификационной категории, МОУ лицей №88, г. Екатеринбург.
Математика 10 класс
Проводится в честь Эндрю Уайлса
Время выполнения работы 1 час 30 минут
__________ _______ _________ ___________ ________ __________ ______________
Фамилия Имя Отчество Нас. Пункт Область ОУ № Код участника
Таблица ответов
| Задание | ||||||||||||||||||
| Задание | ||||||||||||||||||
| Задание | ||||||||||||||||||
| Задание | ||||||||||||||||||
| Задание | ||||||||||||||||||
| Задание | ||||||||||||||||||
| Задание | ||||||||||||||||||
| Задание | ||||||||||||||||||
| Задание | ||||||||||||||||||
| Задание | ||||||||||||||||||
| Задание | ||||||||||||||||||
| Задание | ||||||||||||||||||
| Задание | ||||||||||||||||||
| Задание | ||||||||||||||||||
| Задание | 15.1 | |||||||||||||||||
| Задание | 15.2 | |||||||||||||||||
| Задание | 15.3 | |||||||||||||||||
| Задание | 15.4 | |||||||||||||||||
| Задание | 16.1 | |||||||||||||||||
| Задание | 16.2 | |||||||||||||||||
| Задание | 16.3 | |||||||||||||||||
| Задание | 16.4 |
Инструкция по выполнению работы
Часть 1 состоит из 5 заданий (1-5), оцениваемых в 3 балла.
Часть 2 состоит из 5 заданий (6-10), оцениваемых в 5 баллов.
Часть 3 состоит из 5 наиболее сложных заданий (11-15), оцениваемых в 8 баллов.
Часть 4 состоит из 1 составного задания (16) открытого типа, оцениваемого в 20 баллов. В составном задании 4 подзадания, оцениваемых в 5 баллов.
Баллы, полученные вами за выполненные задания, суммируются. Постарайтесь выполнить как можно больше заданий и набрать наибольшее количество баллов. Внимательно прочитайте каждое задание и проанализируйте все варианты предложенных ответов.
Постарайтесь выполнять задания в том порядке, в котором они даны. Для экономии времени пропускайте задание, которое не удается выполнить сразу, и переходите к следующему. К пропущенному заданию вы сможете вернуться после выполнения всей работы, если останется время.
Ответы занесите в специальную таблицу ответов.
Первая часть. Задания, оцениваемые в 3 балла.
В заданиях 1-5 выберите три правильных ответа из шести предложенных и укажите их номера в таблице ответов.
1. Выберите из данных чисел иррациональные:
1) 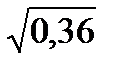
| 4) 
|
2) 
| 5) 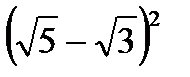
|
3) 
| 6) 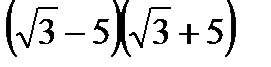
|
2. Выберите верные утверждения относительно чисел a и b, расположенных на числовой прямой:

1) 
| 4) 
|
2) 
| 5) 
|
3) 
| 6) 
|
3. На каких развертках куба закрашенные квадратики являются его противоположными гранями?

4. Определите, в каких предложениях речь идет об остроугольных треугольниках:
1) Сумма любых двух углов этого треугольника больше 900
2) Каждый угол этого треугольника меньше суммы двух других углов
3) Медиана этого треугольника, проведенная к одной из сторон, равна половине этой стороны
4) Величины углов этого треугольника относятся как 1:3:5
5) В этом треугольнике центры вписанной и описанной окружностей совпадают
6) В этом треугольнике есть угол, меньший разности двух других углов
5. Определите, какие из утверждений стереометрии являются верными:
1) Через точку, не лежащую на данной прямой, можно провести более одной прямой, перпендикулярной данной
2) Если прямая лежит в одной плоскости и параллельна другой плоскости, то плоскости параллельны
3) Если две плоскости параллельны, то прямая, лежащая в одной из этих плоскостей, параллельна другой плоскости
4) Если две плоскости перпендикулярны, и прямая лежит в одной из этих плоскостей, то она не обязательно перпендикулярна другой плоскости
5) Прямая, перпендикулярная линии пересечения двух плоскостей и лежащая в одной из них, перпендикулярна другой плоскости
6) Прямая, пересекающая круг в центре и перпендикулярная его диаметру, перпендикулярна плоскости круга