Достаточные условия условного экстремума

Рассмотрим кривую 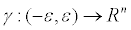, лежащую на поверхности F и проходящую через точку , 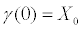. Если функция одной переменной 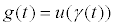в точке 0 будет иметь минимум, независимо от выбора кривой 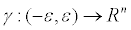, то, очевидно, точка будет являтся точкой условного локального минимума функции ..Для того, чтобы точка t = 0 была точкой минимума функции 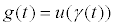, достаточно, чтобы выполнялись условия

.

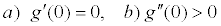
Пусть 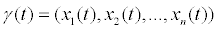. Тогда имеем

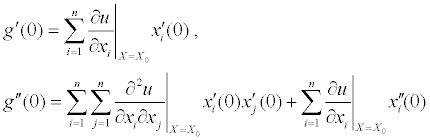
Поскольку кривая 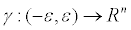лежит на поверхности F, то мы имеем m тождеств

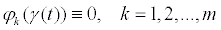. Используя эти тождества, получаем

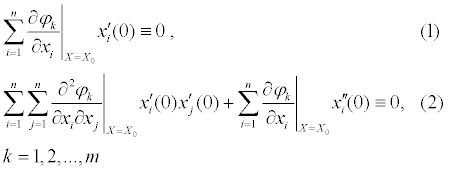
Из (1) следует, чтобы выполнялось условие a) достаточно, чтобы являлся линейной комбинацией градиентов

.

Итак, пусть 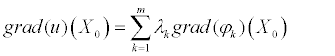, т.е. 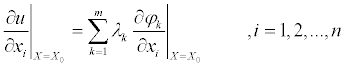(3)

Умножим k-oe тождество (2) на 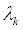и просумvируем по индексу k. В результате, используя (3), получим

 

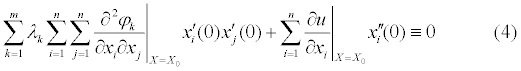
Выражая сумму 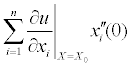из (4) и подставляя в выражение для второй производной

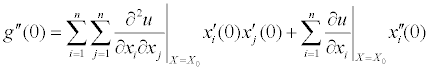, получаем

 

. .

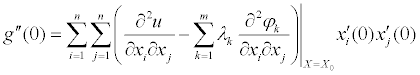Следовательно, для того чтобы выполнялось условие б) достаточно, чтобы выполнялось неравенство

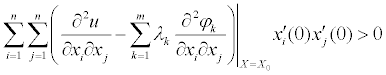для любого ненулевого вектора

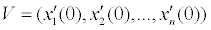, удовлетворяющего системе уравнений

.

 

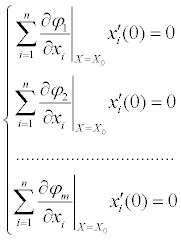№24 Алгоритм нахождения условного экстремума.

№25 Численные методы поиска безусловного экстремума. Скорость сходимости итерационных методов.

Требуется найти безусловный минимум функции f(x) одной переменной, то есть такую точку х^*, что f(х^*) = min f(x).

Поставленная задача одномерной минимизации может быть решена с помощью необходимых и достаточных условий безусловного экстремума. Однако проблема получения решения уравнения df(x)/dx = 0 может оказаться весьма сложной. Более того, в практических задачах функция f(x)

Может быть не задана в аналитическом виде или часто неизвестно, является ли она дифференцируемой. Поэтому получение численного решения поставленной задачи является актуальным.

Для методов одномерной минимизации типично задание априорной информации о положении точки минимума с помощью начального интервала неопределенности. Предполагается, что точка минимума принадлежит интервалу, но ее точное значение неизвестно. Большинство известных методов одномерной минимизации применяется для класса унимодальных функций.

Существуют две принципиально различные стратегии выбора точек, в которых производится вычисление значений функции. Если все точки задаются заранее, до вычислений, - это пассивная(параллельная) стратегия. Если эти точки выбираются последовательно в процессе поиска с учетом результатов предыдущих вычислений, - это последовательная стратегии.

Последовательную стратегию можно реализовать следующими способами:

а) применением квадратичной и кубической интерполяции, где по нескольким вычисленным значениям функции строится интерполяционный полином, а его минимум указывает на очередное приближение искомой точки экстремума;

б) построением последовательности вложенных друг в друга интервалов, каждый из которых содержит точку минимума,

Стратегия поиска включает в себя 3 этапа:

1) Выбор начального интервала неопределенности. Границы интервала должны быть такими, чтобы функция была унимодальной.

2) Уменьшение интервала неопределенности.

3) Проверку условия окончания. Поиск заканчивается, когда длина текущего интервала неопределенности оказывается меньне установленной величины

Ответом является множество точек, принадлежащих последнему интервалу неопределенности, которых каким-либо образом выбирается решение задачи.

№26 Методы одномерный минимизации нулевого порядка. Стратегии поиска.

№27 Алгоритм Свенна для выбора начального интервала неопределенности.

Для эвристического выбора начального интервала неопределенности применяют алгоритм Свенна:

1) задаются следующие параметры: некоторая точка х⁰, величина шага t>0,

полагаем k=0

2) вычисляем значения функции в трех точках f(x⁰-t), f(x⁰), f(x⁰+t),

3) проверяем условие окончания:

a) если f(x⁰-t) ≥ f(x⁰) ≤ f(x⁰+t),то начальный интервал неопределенности найден: [a₀, b₀] = [x⁰-t, x⁰+t]

б) если f(x⁰-t) ≤ f(x⁰) ≥ f(x⁰+t), то функция не является унимодальной, а требуемый интервал неопределенности не может быть найден, вычисления при этом прекращаются, рекомендуется задать другую начальную точку.

в) если условие окончания не выполняется, то переходят к шагу 4

4) определяем величину D:

а) если f(x⁰-t) ≥ f(x⁰) ≥ f(x⁰+t), то D= t, a₀= x⁰, x¹= x⁰+ t, k=1

б) если f(x⁰-t) ≤ f(x⁰) ≤ f(x⁰+t), то D= -t, b₀= x⁰, x¹= x⁰- t, k=1

5) находим следующую точку x^k+1= x^k + 2^k D

6) проверяем условие убывания функции:

а) если f(x^k+1) < f(x^k) и D= t, то a₀ = x^k

б) если f(x^k+1) < f(x^k) и D= -t, то b₀ = x^k

в обоих случаях положить k= k+1 и перейти к шагу 5

в) если f(x^k+1) ≥ f(x^k), то процедура завершена При D= t положить

b₀ = x^k+1, а при D= -t положить а₀ = x^k+1. В результате имеем исходный начальный интервал неопределенности.

Уменьшение интервала неопределенности, осуществляемое при использовании последовательной стратегии, производится на основании вычисления функции в двух точках текущего интервала. Свойство унимодальности позволяет определить, в каком из возможных подынтервалов точка минимума отсутствует.

 

№28 Метод равномерного поиска и метод деления интервала пополам.

 

 

 

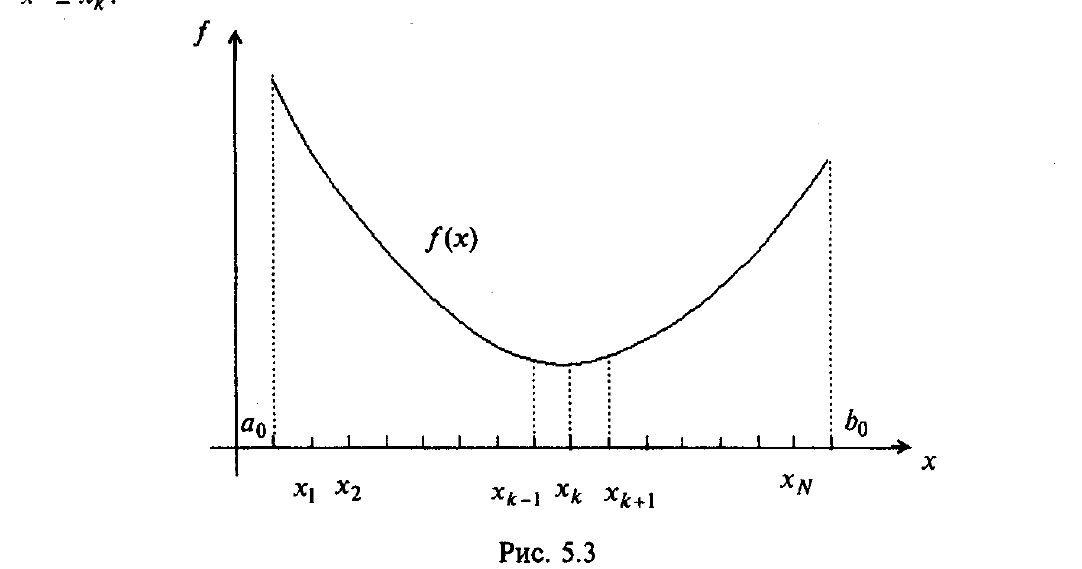
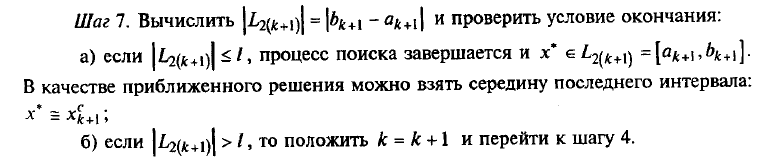
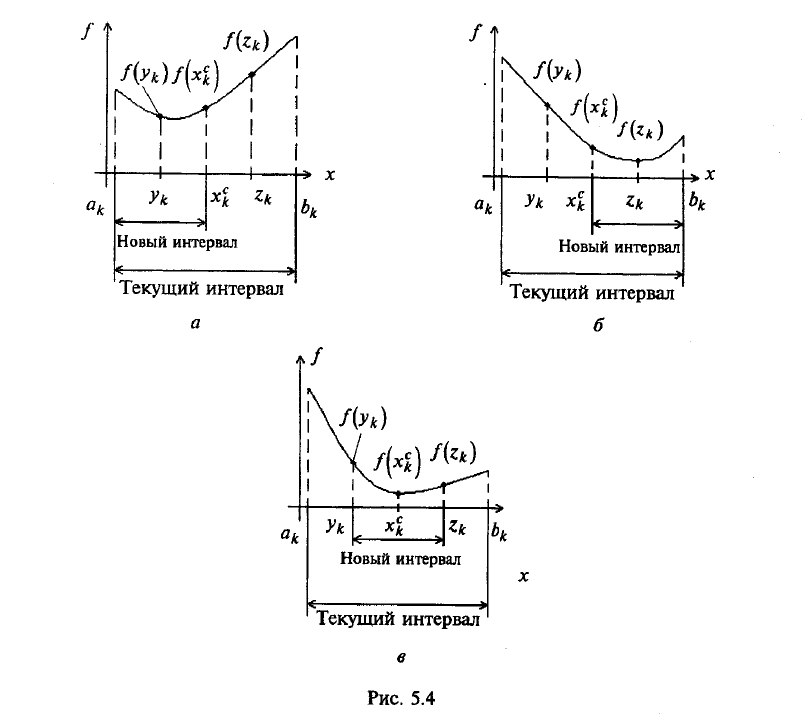
Метод деления отрезка пополам относится к последовательным стратегиям и позволяет исключить из дальнейшего рассмотрения на кажодой итерации в точности и половину текущего интервала неопределенности. Задается начальный интервал неопределенности, а алгоритм основан на анализе величин функции в трех точках, равномерно распределенных на текущем интервале и делящих его на 4 равные части. Условие окончания процесса стандартное: поиск заканчивается, когда длина текущего интервала неопределенности оказывается меньше установленной величины.

 

№29 Метод дихотомии и метод «золотого сечения».

Метод 1.Метод деления интервала пополам (метод дихотомии).

Этот метод позволяет исключать в точности половину интервала на каждой итерации.

Приведем описание поисковой процедуры, ориентированной на нахождение точки минимума функции f(x) в интервале (a,b).

Шаг1. Положить.

x_m=(a+b)/2 и L=b-a.

Вычислить значение f(x_m).

Шаг2. Положить.

x₁=a+L/4 и x₂=b-L/4.

Можно заметить, что точки x₁,x_m,x₂ делят интервал (a,b) на четыре равные части.

Вычислить значения f(x₁) и f(x₂).

Шаг3. Сравнить f(x₁) и f(x₂).

(1) если f(x₁)<f(x_m), исключить интервал (x_m,b), положив b=x_m.

Средней точкой нового интервала поиска становится точка x₁. Следовательно, необходимо положить x_m=x₁. Перейти к шагу 5.

(2) если f(x₁)³f(x_m), перейти к шагу 4.

Шаг4. Сравнить f(x₂) и f(x_m).

(1) если f(x₂)<f(x_m),исключить интервал (a,x_m), положив a=x_m.

Т.к. средней точкой нового интервала становится точка x₂, положить x_m=x₂.

Перейти к шагу 5.

(2) если f(x₂)³f(x_m), исключить интервалы (a,x₁) и (x₂,b).

Положить a=x₁ и b=x₂.

(Заметим, что x_m продолжает оставаться средней точкой нового интервала)

Перейти к шагу 5.

Шаг5. Вычислить L=b-a.

Если величина |L| мала, закончить поиск, в противном случае вернуться к шагу 2.

Пример. Метод деления интервала пополам.

Минимизировать f(x)=(100-x)² в интервале 60£x£150.

Здесь a=60, b=150, L=150-60=90, x_m=(60+150)/2=105.

Итерация 1.

x₁=a+(L/4)=60+(90/4)=82.5

x₂=b-(L/4)=150-(90/4)=127.5

f(82.5)=306.25>f(105)=25

f(127.5)=756.25>f(105)

Таким образом, исключаются интервалы (60;82.5) и (127.5;150).

Длина интервала поиска уменьшается с 90 до 45.

Итерация 2.

a = 85.5, b = 127.5, x_m = 105, L = 127.5-82.5 = 45.

x₁ = 82.5+(45/4) = 93.75

x₂ = 127.5-(45/4) = 116.25

f(93.75) = 39.06>f(105)=25

f(116.25) = 264.06>f(105).

Таким образом, интервал неопределенности равен (93.75;116.25).

Итерация 3.

a = 93.75, b = 116.25, x_m = 105, L = 116.25-93.75 = 22.5

x₁=99.375, x₂=110.625

f(x₁) = 0.39<f(105) = 25.

Таким образом, исключается интервал (105,116.25).

Новый интервал неопределенности равен (93.75,105), его средняя точка 99.375 (точка х₁ на итерации 3).

 

Требуется найти безусловный минимум функции одной переменной.

Для построения конкретного метода «золотого сечения », работающего по принципу последовательного сокращения интервала неопределенности, следует задать правило выбора на каждом шаге двух внутренних точек. Желательно, чтобы одна и з них всегда использовалась в качестве внутренней и для следующего интервала. Тогда число вычислений функции сократится вдвое и одна итерация потребует расчета только одно нового значение функции. В методе золотого сечения в качестве двух внутренних точек выбираются точки золотого сечения.

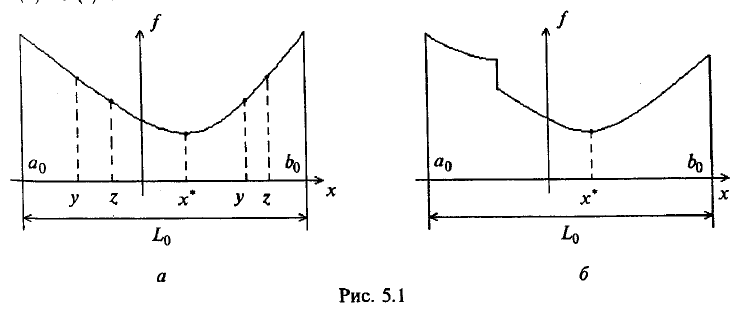
Точка производит «золотое сечение» отрезка, если отношение длины всего отрезка к большей части равно отношению большей части к меньшей.

На отрезке [a, b] имеется две симметричные относительно его концов точки y и z_.

_______________________

a y z b

 

При этом выполняются соотношения:

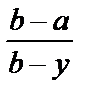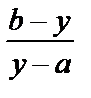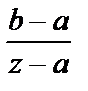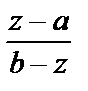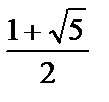= = = = @ 1,618

Кроме того, точка y производит золотое сечение отрезка [a, z], а точка z - отрезка [у, b]

 

Метод относится к последовательным стратегиям. Задается начальный интервал неопределенности и требуемая точность. Алгоритм уменьшения интервала опирается на анализ значений функции в двух точках. В качестве точек вычисления функции выбираются точки золотого сечения. Тогда с учетом свойств золотого сечения на каждой итерации, кроме первой, требуется только одно новое вычисление функции. Условия окончания процесса поиска стандартные: поиск заканчивается, когда длина текущего интервала не определенности оказывается меньше установленной величины.

Алгоритм.

1) Задается начальный интервал неопределенности [a₀, b₀], точность - l>0

2) Полагаем k=0

3) Вычисляем

y₀ = a₀ + (b₀ - a₀) 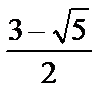z₀ = a₀ + b₀ - y₀ 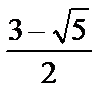= 0?38196

4) Вычисляем f(y_k), f(z_k).

5) Сравниваем f(y_k), f(z_k).

а) если f(y_k) ≤ f(z_k), то a_k+1 = a_k, b_k+1 = z_k, переходим к шагу 6.

б) если f(y_k) > f(z_k), то a_k+1 = y_k, b_k+1 = b_k,

y_k+1 = z_k, z_k+1 = a_k+1 + b_k+1 - z_k

6) Вычисляем D = | a_k+1 - b_k+1| и проверяем условие окончания

а) если D < l, то процесс завершается и в качестве приближенного решения берут середину последнего интервала.

б) если D > l, то полагаем k+1 = k и переходим к шагу 4.

 

Для метода золотого сечения характеристика относительного уменьшения начального интервала неопределенности находится по формуле

R(N) = (0,618)^N-1, где N - количество вычислений функции.