Дана функция
f(x)=5x6 - 36x5 + (162/2)x4 - 60x3 + 36,определенная на всей действительной оси. Определить точки локальных минимумов и максимумов.
Вычисляем:
df/dx=30x5 – 180x4 + 330x3 – 180x2 = 30x2(x-1)(x-2)(x-3)
Первая производная обращается в нуль в точках x=0,1,2,3-это стационарные точки.
Для проверки выполнения достаточных условий экстремума и необходимых условий второго порядка используются два способа.
Критерий проверки достаточных условий экстремума (критерий Сильвестра)
1) Для того чтобы матрица Гессе H(x*) была положительно определенной (H(x*)>0) и точка x* являлась точкой локального минимума, необходимо и достаточно, чтобы знаки угловых миноров были строго положительны, то есть:
D1>0, D2>0, …, Dn>0
2) Для того чтобы матрица Гессе H(x*) была отрицательно определенной (H(x*)<0) и точка x* являлась точкой локального максимума, необходимо и достаточно, чтобы знаки угловых миноров чередовалис, начиная с отрицательного
D1<0, D2>0, D3<0,…, (-1)nDn>0
Критической (стационарной) точкой дифференцируемой функции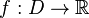 
, где 
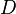— область в 
, называется точка, в которой все её частные производные обращаются в ноль.
Критическая точка называется невырожденной, если в ней 
отлично от нуля.
Непрерывно дифференцируемая функция 
, определенная во всем пространстве или в его открытом подмножестве, может достигать локального максимума (минимума) только в критических точках, причем если точка невырождена, то матрица 
в ней должна быть отрицательно (положительно)определённой.
Достаточные условия экстремума.
1) Пусть функция дифференцируема в некоторой окрестности точки x 0, кроме, быть может, самой этой точки, и непрерывна в точке x 0. Если производная функции меняет знак с минуса на плюс при переходе через эту точку слева направо, то x 0 – точка минимума. Если производная функции меняет знак с плюса на минус при переходе через эту точку слева направо, то x 0 – точка максимума.
2) Пусть 
– стационарная точка функции f (x), и существует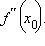 
Если 
то – точка минимума; если 
то – точка максимума функции f (x).
№21 Нахождение условного экстремума. Обобщенная и классическая функции Лагранжа.
№22 Необходимые условия 1-го и 2-го порядков.
Утверждение 1. (необходимые условия экстремума первого порядка)
Пусть x* является точкой локального минимума (максимума) функции
f(x) на множестве Rn и f(x) дифференцируема в точке x*. Тогда градиент функции f(x) в точке x* равен нулю, то есть
Ñ f(x*) = 0 (1)
или
= 0, i=1, …,n (2)
Точки x*, удовлетворяющие условиям (1) или (2), называются стационарными.
Критерий проверки достаточных условий экстремума (критерий Сильвестра)
1) Для того чтобы матрица Гессе H(x*) была положительно определенной (H(x*)>0) и точка x* являлась точкой локального минимума, необходимо и достаточно, чтобы знаки угловых миноров были строго положительны, то есть:
D1>0, D2>0, …, Dn>0
2) Для того чтобы матрица Гессе H(x*) была отрицательно определенной (H(x*)<0) и точка x* являлась точкой локального максимума, необходимо и достаточно, чтобы знаки угловых миноров чередовалис, начиная с отрицательного
D1<0, D2>0, D3<0,…, (-1)nDn>0
Условный экстремум
Пусть 
-открытое множество, 
- система непрерывно дифференцируемых функций,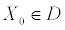 
.
Система уравнений
(***)
задает в окрестности точки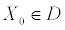 
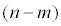-мерную гладкую поверхность F в 
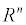, если
в точке 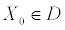система градиентов 
линейно независима.
Точка 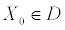называется точкой локального условного максимума (минимума) функции 
относительно уравнений связи (***), если
существует такое 
, что для точек 
поверхности F при 
выполняется неравенство 
.
Необходимое условие условного экстремума
Для того, чтобы точка 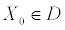была точкой локального условного максимума (минимума) функции относительно уравнений
связи задающих 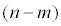-мерную гладкую поверхность F в окрестности данной точки
необходимо, чтобы эта точка удовлетворяла системе уранений Лагранжа
,
где 
некоторые числа.
Доказательство. Действительно, если точка 
лежит на поверхности F и градиент 
не является линейной комбинацией градиентов
, то поверхность уровня 
пересекает F трансверсально (под ненулевым углом). Отсюда следует, что точка не может быть точкой минимума или максимума.
№23 Достаточные условия условного экстремума.