Логические выражения и таблицы истинности.
Каждое составное высказывание можно выразить в виде формулы (логического выражения), в которую войдут логические переменные, обозначающие высказывания, и знаки логических операций, обозначающие логические функции.
Для записи составных высказываний в виде логических выражений на формальном языке (языке алгебры логики) в составном высказывании нужно выделить простые высказывания и логические связи между ними.
Запишем в форме логического выражения составное высказывание «2х2=5 или 2х2=4 и 2х2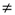 
5 или 2х2 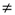4». Проанализируем составное высказывание. Оно состоит из двух простых высказываний:
А = «2х2=5» - ложно (0),
В = «2х2=4» - истинно (1).
Тогда составное высказывание можно записать в следующей форме:
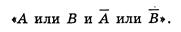
Теперь необходимо записать высказывание в форме логического выражения с учетом последовательности выполнения логических операций (см. таблицу).
Порядок следования логических операций:
| Логическая функция | Операция | Связки | Знаки | Правило |
| Инверсия | отрицание | НЕ |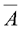 
| 1→0 0→1 |
| Конъюнкция | умножение | И | & или ^ | 0*0=0 1*0=0 0*1=0 1*1=1 |
| Дизъюнкция | логическое сложение | ИЛИ | v или + | 0+0=0 1+0=1 0+1=1 1+1=1 |
| Импликация | следование | если…, то … из … следует …влечет… | → | 0=1→0 |
| Эквиваленция | равенство или двойная импликация | тогда и только тогда необходимо и достаточно, …равносильно… | ↔ или ~ | 1=1↔1 1=0↔0 |
При выполнении логических операций определен следующий порядок их выполнения: инверсия, конъюнкция, дизъюнкция, следования, равенства. Для изменения указанного порядка могут использоваться скобки.
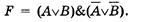
Истинность или ложность составных высказываний можно определять чисто формально, руководствуясь законами алгебры высказываний, не обращаясь к смысловому содержанию высказываний.
|
|
Подставим в логическое выражение значения логических переменных и, используя таблицы истинности базовых логических операций, получим значение логической функции:
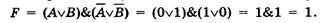
Для каждого составного высказывания (логического выражения) можно построить таблицу истинности, которая определяет его истинность или ложность при всех возможных комбинациях исходных значений простых высказываний (логических переменных).
При построении таблиц истинности целесообразно руководствоваться определенной последовательностью действий.
Во-первых, необходимо определить количество строк в таблице истинности, которое равно количеству возможных комбинаций значений логических переменных, входящих в логическое выражение. Если количество логических переменных n, то:
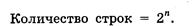
В нашем случае логическая функция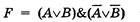 
имеет две переменные и, следовательно, количество строк в таблице истинности должно быть равно 4.
Во-вторых, необходимо определить количество столбцов в таблице истинности, которое равно количеству логических переменных плюс количество логических операций. В нашем случае количество переменных равно двум, а количество логических операций равно пяти, т.е. количество столбцов таблицы истинности равно семи.
В-третьих, необходимо построить таблицу истинности с указанным количеством строк и столбцов, обозначить столбцы и внести возможные наборы значений исходных логических переменных.
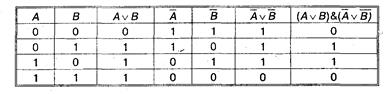
В-четвертых, необходимо заполнить таблицу истинности по столбцам, выполняя базовые логические операции в необходимой последовательности и в соответствии с их таблицами истинности. Теперь мы можем определить значение логической функции для любого набора значений логических переменных.
|
|
Логические выражения, у которых таблицы истинности совпадают, называются равносильными. Для обозначения равносильных логических выражений используется знак «=».
Докажем, что логические выражения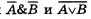 
равносильны. Построим сначала таблицу истинности для логического выражения 
.
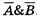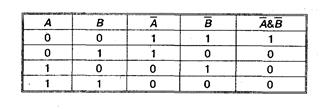
Построим теперь таблицу истинности для логического выражения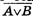 
.
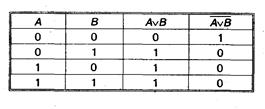
Таблицы истинности совпадают, следовательно, логические выражения равносильны:
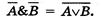
Итак, чтобы составить таблицу истинности для логической формулы, надо выполнить следующие шаги:
1. подсчитать количество переменных n в логическом выражении
2. определить число строк в таблице, которое равно Q = 2n
3. подсчитать количество логических операций в логическом выражении и определить количество столбцов в таблице, которое равно количеству переменных плюс количество операций
4. ввести названия столбцов таблицы в соответствии с последовательностью выполнения логических операций с учётом скобок и приоритетов
5. заполнить столбцы входных переменных наборами значений
6. провести заполнение таблицы истинности по столбцам, выполняя логические операции в соответствии с установленной в п. 4 последовательностью.
| Переменные | Промежуточные логические формулы | Формула | ||||||
| x | y | z |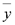 
| 
| 
| 
| 
| 
|
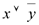
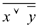
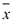
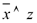
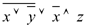
Пример (см. выше):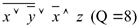 
|
|
Данная формула является выполнимой, так как в некоторых случаях принимает значение «истина», а в некоторых – «ложь».
Задание:
Записать составное высказывание «(2*2=4 и 3*3=9) или (2*2≠4 и 3*3≠9)» в форме логического выражения. Построить таблицу истинности.