Тела, участвующие в теплообмене, представляют собой термодинамическую систему. Термодинамическая система называется теплоизолированной, если она не получает энергию извне и не отдаёт её; теплообмен происходит только между телами, входящими в эту систему. Для любой теплоизолированной системы тел справедливо следующее утверждение: количество теплоты, отданное одними телами, равно количеству теплоты, принимаемому другими телами.
Qотд . = Qполуч .(5)
Это утверждение описывает частный случай закона сохранения и превращения энергии в применении к процессу теплообмена. А формула (5) является одним из видов уравнения теплового баланса.
При решении задач с помощью данного вида уравнения теплового баланса в формуле (1) в качестве t2 следует брать большую температуру, а в качестве t1 – меньшую. Тогда разность (t2 – t1) будет положительна и всё произведение cm(t2–t1) также будет положительным. Все теплоты, отданные и полученные, будут положительными.
Уравнение теплового баланса можно записать и в таком виде:
Q1+ Q2+…+ Qn= 0,(6)
Где n – количество тел системы.
Алгебраическая сумма всех количеств теплоты (поглощенных и выделенных) в теплоизолированной системе равна нулю.
Q1, Q2, …, Qn – это теплоты, поглощаемые или выделяемые участниками теплообмена. Очевидно, что в этом случае какие-то теплоты должны быть положительны, а какие-то – отрицательны. При записи уравнения теплового баланса в виде (6) всегда t2 – конечная температура, а t1 – начальная.
Если тело нагревается, то разность (t2 – t1) положительна и все произведение cm(t2 – t1) положительно. То есть Q > 0 тогда, когда теплота к данному телу подводится.
А если t2 < t1 (тело остывает), то разность (t2 – t1) отрицательна, то есть Q < 0. В этом случае тело энергию выделяет.
Если при фазовом переходе энергия к телу подводится (плавление, кипение), то Q > 0; если тело выделяет энергию (кристаллизация, конденсация), то Q < 0.
В принципе уравнения (5) и (6) равносильны. Результат решения задачи не зависит от того, каким видом уравнения пользуемся. Выбор способа решения – за читателем.
Применим уравнение теплового баланса для решения ряда задач.
Задача 1
В медном калориметре массой 100 г находится 1 кг воды при температуре 20°С. В воду опускают свинцовую деталь массой 2 кг, имеющую температуру 90°С. До какой температуры нагреется вода? Потерями теплоты пренебречь.*
Решение
 m1 = 0,1 кг
с1= 380 Дж/(кг×0С)
t2 = 20°С
m2 = 1 кг
с2=4200 Дж/(кг×0С)
m3 = 2 кг
с3= 140 Дж/(кг×0С)
t3 = 90°С
q –? m1 = 0,1 кг
с1= 380 Дж/(кг×0С)
t2 = 20°С
m2 = 1 кг
с2=4200 Дж/(кг×0С)
m3 = 2 кг
с3= 140 Дж/(кг×0С)
t3 = 90°С
q –?
| Проведём анализ: Вода и калориметр находились в тепловом равновесии, поэтому они имели одинаковую температуру: t1 = t2 = 20°С. При опускании в воду с температурой 20°С свинцового тела с температурой 90°С между водой и свинцом будет происходить теплообмен. Свинец будет остывать, а вода - нагреваться. В этом же процессе участвует и калориметр, который, как и вода, будет тоже нагреваться. |
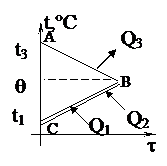
| Изменение температур тел с течением времени удобно изображать на графике зависимости t(t). Отрезок АВ соответствует графику изменения температуры свинцового тела. Стрелка, идущая от него, показывает, что, остывая, свинец выделяет энергию Q3. |
| Два параллельных отрезка СВ соответствуют графикам изменения температур калориметра и воды. Стрелки, идущие к ним, показывают, что для нагревания калориметра и воды требуется энергия Q1 и Q2, которую они поглощают. | |
Решим задачу с использованием уравнения теплового баланса в виде (5):
Q1 + Q2 = Q3,
c1m1(q - t1) + c2m2(q - t2) = c3m3(t3 - q).
Выражаем температуру q:
q = 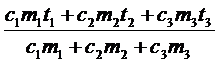
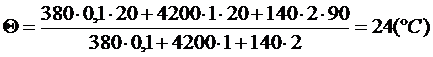
|
Решим задачу с использованием уравнения теплового баланса в виде (6):
Q1 + Q2 + Q3 = 0,
c1m1(q - t1) + c2m2(q - t2) + c3m3(q - t3) = 0.
q = 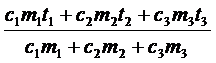 = 24 (°С)
= 24 (°С)
Ответ: Вода нагреется до 24 °С.
Предлагаю читателю самостоятельно сделать проверку размерности.
Задача 2
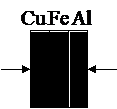 Три пластины: медную, имеющую массу m1 = 1 кг и температуру t1 = 100°С, железную (m2 = 1,2 кг, t2 = 150°С) и алюминиевую (m3 = 0,8 кг, t3 = 80°С) сложили вплотную (см рис). Какую температуру будут иметь пластины, когда теплообмен прекратится? Потерями теплоты в окружающую среду пренебречь.
Три пластины: медную, имеющую массу m1 = 1 кг и температуру t1 = 100°С, железную (m2 = 1,2 кг, t2 = 150°С) и алюминиевую (m3 = 0,8 кг, t3 = 80°С) сложили вплотную (см рис). Какую температуру будут иметь пластины, когда теплообмен прекратится? Потерями теплоты в окружающую среду пренебречь.
| m1 = 1 кг с1= 380 Дж/(кг×0С) t1 = 100°С m2 = 1,2 кг с2= 460 Дж/(кг×0С) t2 = 150°С m3 = 0,8 кг с3= 920 Дж/(кг×0С) t3 = 80°С | Решение
Решим задачу с помощью уравнения теплового баланса в виде (5).
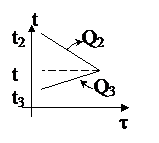 1. Не трудно догадаться, что в результате теплообмена самая горячая пластина остынет, а самая холодная - нагреется. Итак, мы знаем, что будет происходить с железной и алюминиевой пластинами: железная будет остывать, алюминиевая – нагреваться.
Мысленно соединим сначала эти две пластины и найдём температуру t, которой они при этом достигнут:
Q2 = Q3 Þ
c2m2(t2 - t) = c3m3(t - t3)
t = 1. Не трудно догадаться, что в результате теплообмена самая горячая пластина остынет, а самая холодная - нагреется. Итак, мы знаем, что будет происходить с железной и алюминиевой пластинами: железная будет остывать, алюминиевая – нагреваться.
Мысленно соединим сначала эти две пластины и найдём температуру t, которой они при этом достигнут:
Q2 = Q3 Þ
c2m2(t2 - t) = c3m3(t - t3)
t = 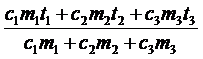
|
| q -? |
t = 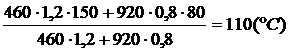
2. Теперь медная пластина вступает в теплообмен с железной и алюминиевой. Медная будет нагреваться от температуры t1 до температуры q, а железная и алюминиевая – остывать от температуры t до температуры q. Тогда:
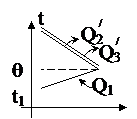 Q1 = Q2'+ Q3',
Q1 = Q2'+ Q3',
c1m1(q - t1) = (c2m2 + c3m3)(t - q),
c1m1q – c1m1t1 = (c2m2 + c3m3)t – (c2m2 + c3m3)q
q = 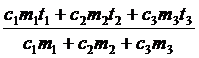
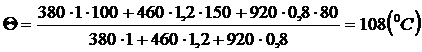
3. Решим задачу, применив уравнение теплового баланса в виде (6):
Q1 + Q2 + Q3 = 0,
c1m1(q - t1) + c2m2(q – t2) + c3m3(q - t3) = 0,
q = 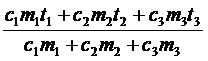 = 108 (°С)
= 108 (°С)
Ответ: Пластины будут иметь температуру 108 °С.
Как видим, второй способ оказался и в данном случае более рациональным. Однако, первый способ зачастую оказывается более понятным, особенно при наличии фазовых переходов. Поэтому в дальнейшем автор будет придерживаться первого способа решения задач. Желательно, чтобы читатель пробовал решать их и вторым способом.
Задача 3
В железном ведре массой 1,2 кг находится 5 кг воды при температуре 20°С. Сколько льда температурой – 10°С надо положить в ведро, чтобы температура воды понизилась до 12°С? Теплообменом с окружающей средой пренебречь.
m1 = 1,2 кг
с1=460 Дж/(кг×0С)
m2 = 5 кг
с2=4200 Дж/(кг×0С)
t1 = t2 = 20°С
t3 = -10°С
с3=2100 Дж/(кг×0С)
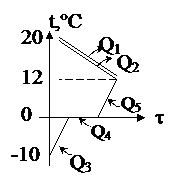 t4 = 0оС
q = 12°С t4 = 0оС
q = 12°С
| Решение Известна конечная температура, Значит, анализ ситуации довольно прост: вода и ведро будут остывать, не испытывая фазовых переходов, отдавая теплоты Q1 и Q2, а лёд сначала будет нагреваться до температуры плавления t4, поглощая теплоту Q3, затем плавиться, поглощая теплоту Q4, а затем вода, образовавшаяся из льда, будет нагреваться до конечной температуры q, поглощая теплоту Q5. Так как иных участников теплообмена нет, то можно так записать уравнение теплового баланса: Q1 + Q2 = Q3 + Q4 + Q5. (c1m1 + c2m2)(t1 - q) = = c3m3(t4 - t3) + lm3 + c2m3(q - t4) |
| m3 –? |
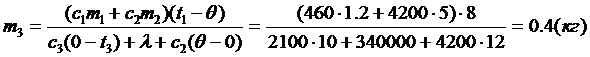
Ответ: Потребуется 0,4 кг льда.
Задача 4
В алюминиевую кастрюлю массой 200 г, содержащую 3 кг воды при 20°С, поместили стальную деталь массой 0,5 кг, нагретую до 500°С. При этом часть воды выкипела, а оставшаяся вода нагрелась до 22°С. Сколько воды выкипело?

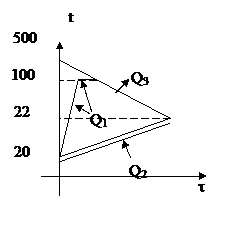 m1 = 3 кг
с1=4200Дж/(кг°С)
m2 = 0,2 кг
с2 =920 Дж/(кг°С)
t1 = t2 = 20°С
q = 22°С
m3 = 0,5 кг
с3 = 460 Дж/(кг0С)
t3 = 500°С
L = 2,3×106 Дж/кг m1 = 3 кг
с1=4200Дж/(кг°С)
m2 = 0,2 кг
с2 =920 Дж/(кг°С)
t1 = t2 = 20°С
q = 22°С
m3 = 0,5 кг
с3 = 460 Дж/(кг0С)
t3 = 500°С
L = 2,3×106 Дж/кг
| Решение 1. Стальная деталь, не претерпевая фазовых переходов, остыла от 500°С до 22°С, выделив при этом количество теплоты Q3 = c3m3(t3 - q). 2. Часть воды массой m0 нагрелась до температуры кипения (100оС) и выкипела. При этом была поглощена теплота Q1 = c1m0(100 - t1) + Lm0. 3. Оставшаяся в кастрюле вода массой (m1 - m0) и сама кастрюля массой m2 нагрелись от 200С до 22°С. При этом была поглощена теплота Q2 = c1(m1 - m0)(q - t1) + c2m2(q - t1). | |
| m0 –? | ||
4. Так как потерь тепла нет, то записываем уравнение теплового баланса:
Q1 + Q2 = Q3,
c1m0(100 - t1) + Lm0 + c1(m1 - m0)(q - t1) +
+ c2m2(q - t2) = c3m3(t3 - q).
5. Решая это уравнение, находим m0:
m0 = 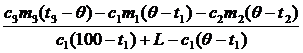 ,
m0 = ,
m0 = 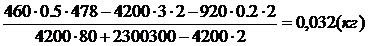 
|
Ответ: Выкипело 32 г воды.
Задача 5
Комок мокрого снега массой 400 г опустили в медный таз массой 500 г, содержащий 2 кг воды при температуре 20°С. После установления теплового равновесия температура воды в тазу стала 10°С. Сколько воды было в комке снега?
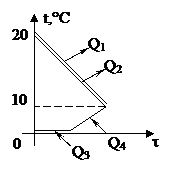 m3 = 0,4 кг
l = 3,4×105 Дж/кг
t1 = t2 = 20°С
t3 = 0°С
m1 = 0,5 кг
с1 = 380 Дж/(кг×0С)
m2 = 2 кг
с2=4200Дж/(кг×0С)
q = 10°С m3 = 0,4 кг
l = 3,4×105 Дж/кг
t1 = t2 = 20°С
t3 = 0°С
m1 = 0,5 кг
с1 = 380 Дж/(кг×0С)
m2 = 2 кг
с2=4200Дж/(кг×0С)
q = 10°С
| Решение 1. Медный таз и вода находятся в тепловом равновесии. Поэтому 20°С – их общая температура. При остывании от 20°С до 10°С ни медь, ни вода фазовых превращений не испытывают. При этом они отдают суммарную теплоту: Q1 + Q2 = c1m1(t1 - q) + c2m2(t2 - q). 2. Мокрый снег – это снег, содержащий воду. Значит, снег и вода находятся в тепловом равновесии. Это возможно только при температуре фазового перехода, то есть при 0°С. | |
| mв –? | ||
Итак, начальная температура мокрого снега 0°С.
3. На пути к температуре 10°С снег массой m3-mв будет сначала таять. Для этого требуется теплота Q3 = l(m3 - mв). А затем вся вода массой m3 будет нагреваться от 0°С до 10°С. Для этого ей надо получить количество теплоты Q4 = c2m3(q - t3).
4. Так как нет потерь тепла, то можно написать уравнение теплового баланса:
Q1 + Q2 = Q3 + Q4,
с1m1(t1 - q) + c2m2(t2 - q) = l(m3 - mв) + c2m2(q - t3).
5. Решая это уравнение, находим mв:
mв = 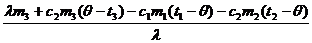 mв =
mв = 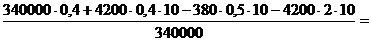 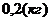 Ответ:В комке мокрого снега было 0,2 кг воды.
Ответ:В комке мокрого снега было 0,2 кг воды.
|
Задача 6
В холодную воду массой 2 кг, имеющую температуру 10°С, находящуюся в кастрюле, влили 3 кг горячей воды при температуре 80°С. До какой температуры нагреется холодная вода, если известно, что 25% теплоты, отданной горячей водой, пошло на нагревание кастрюли? Какова теплоемкость кастрюли?
| M1 = 2 кг t1 = 10°С m2 = 3 кг t2 = 80°С h1=0,25 (25%) | Решение
Так как 25% теплоты отданы кастрюле, то 75% теплоты пошло на нагревание холодной воды. Значит, можно говорить о КПД процесса нагревания холодной воды:
h2 = 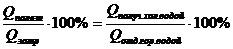 (h2 = 0,75)
Здесь Qполез - теплота, идущая на нагревание холодной воды: Qполез = c1m1(q - t1);
Qзатр - теплота, отданная горячей водой: Qзатр = c2m2(t2 - q).
Удельные теплоты с1 холодной и с2 горячей воды равны.
h2 = (h2 = 0,75)
Здесь Qполез - теплота, идущая на нагревание холодной воды: Qполез = c1m1(q - t1);
Qзатр - теплота, отданная горячей водой: Qзатр = c2m2(t2 - q).
Удельные теплоты с1 холодной и с2 горячей воды равны.
h2 = 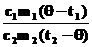 Þ h2m2(t2 - q) = m1(q - t2),
h2m2t2 - h2m2q = m1q - m1t1, Þ h2m2(t2 - q) = m1(q - t2),
h2m2t2 - h2m2q = m1q - m1t1,
|
| q -? С -? |
q = 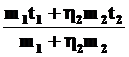
q = 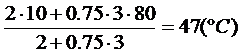
Так как 25% теплоты, отданной горячей водой, пошло на нагревание кастрюли, то можно говорить и о КПД процесса нагревания кастрюли:

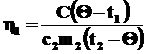 ,
,
откуда: 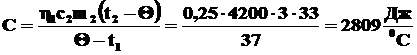
Ответ: Холодная вода нагреется до температуры 47°С. Теплоемкость кастрюли 2809 Дж/0С.
Задача 7
Сколько керосина нужно сжечь, чтобы превратить в пар 1 кг льда, взятого при температуре - 40°С? КПД нагревательного устройства равен 60%, удельная теплота сгорания керосина 46 МДж/кг.
 m1 = 1 кг
t1 = -40°С
с1 =2100Дж/(кг×0С)
l = 3,4×105 Дж/кг
с2 =4200Дж/(кг×0С)
L = 2,3×106 Дж/кг
h = 0,6 (60%) q = 46×106 Дж/кг m1 = 1 кг
t1 = -40°С
с1 =2100Дж/(кг×0С)
l = 3,4×105 Дж/кг
с2 =4200Дж/(кг×0С)
L = 2,3×106 Дж/кг
h = 0,6 (60%) q = 46×106 Дж/кг
| Решение
1. Изобразим на графике t(t) процессы: нагревание льда, плавление льда, нагревание получившейся из льда воды, кипение этой воды. Для осуществления каждого из этих процессов необходим подвод теплоты. Теплоту выделяет керосин в процессе сгорания (на графике не показано).
2. Применим формулу КПД нагревателя:
h = 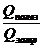 .
Здесь Qполез = Q1 + Q2 + Q3 + Q4 =
= m1[c1(0 - t1) + l + c2(100 - 0) + L],
а Qзатр = qm2.
Получаем: h = .
Здесь Qполез = Q1 + Q2 + Q3 + Q4 =
= m1[c1(0 - t1) + l + c2(100 - 0) + L],
а Qзатр = qm2.
Получаем: h = 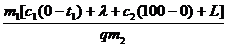 ,
откуда: m2 = ,
откуда: m2 = 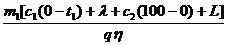 .
m2 = .
m2 = 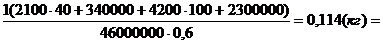 = 114 г
= 114 г
|
| m2 -? |
Ответ: Нужно сжечь 114 г керосина.
Задача 8
Сколько водяного пара, имеющего температуру 120°С, надо впустить в калориметр, содержащий 800 г льда при температуре -20°С, чтобы температура образовавшейся воды оказалась 20°С? Теплоёмкостью калориметра пренебречь.
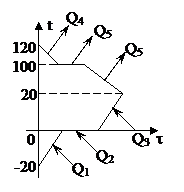 m1 = 0,8 кг
t1 = -20°С
с1 = с2 = 2100
Дж/(кг×0С)
t2 = 120°С
с3 =4200Дж/(кг×0С)
q = 20°С m1 = 0,8 кг
t1 = -20°С
с1 = с2 = 2100
Дж/(кг×0С)
t2 = 120°С
с3 =4200Дж/(кг×0С)
q = 20°С
| Решение 1. Так как теплоемкостью калориметра можно пренебречь, то систему лед - пар можно считать теплоизолированной: теплообмен происходит только между паром и льдом. 2. Получают теплоту тела: - лёд, нагреваясь от –200С до температуры плавления: Q1 = c1m1(0 - t1); - лёд, превращаясь в воду при температуре плавления: Q2 = lm1; - вода, образовавшаяся из льда, нагреваясь от 0°С до 20°С: Q3 = с3m1(q - 0). 3. Отдают теплоту тела: - пар, остывая от 120°С до температуры конденсации: Q4 = c2m2(t2 - 100); - пар, превращаясь в воду при 100°С: Q5 = Lm2; - вода, образовавшаяся из пара, остывая от 100°С до 20°С: Q6 = c3m2(100 - q). 4. Других участников теплообмена нет, поэтому записываем уравнение теплового баланса: Q1 + Q2 + Q3 = Q4 + Q5 + Q6, c1m1(0 – t1) + lm1 + c3m1(q - 0) = c2m2(t2 - 100) + + Lm2 + c3m2(100 - q), |
| m2-? |
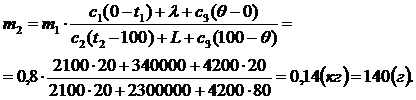
Ответ: Потребуется 140 г водяного пара.
Часто при решении задач можно встретиться со следующей проблемой. В теплообмене участвуют вещества, находящиеся в различных агрегатных состояниях, и конечная температура теплообмена не известна. Тогда уравнение теплового баланса сразу написать не удастся, так как его вид зависит от того, в каких агрегатных состояниях будут находиться конечные продукты. В этом случае последовательность решения задачи немного изменяется. Сначала нужно сделать предварительные расчеты: сколько теплоты выделит или поглотит каждое вещество в предполагаемом процессе, сравнить эти теплоты и сделать вывод о том, в каких агрегатных состояниях будут находиться продукты теплообмена. И только после этого можно записывать уравнение теплового баланса. Такие задачи значительно сложнее задач, в которых конечная температура известна. Рассмотрим ряд таких задач.
Задача 9
В калориметр, содержащий воду массой 0,5 кг при температуре 25°С, впускают водяной пар массой 50 г при температуре 120°С. Какая температура установится в калориметре, если его теплоёмкость 1200 Дж/оС?
 |
| m1 = 0,5 кг с1 =4200 Дж/(кг×0С) t1 = 25°С m2 = 0,05 кг t2 = 120°С c2=2100 Дж/(кг×0С) С = 1200 Дж/0С L = 2,3×106 Дж/кг | Решение
1. Если в конечном итоге весь пар остынет от 120°С до 100°С, затем сконденсируется в воду, затем образовавшаяся из
пара вода остынет от 100°С до q, то в калориметре будет находиться вода при температуре q, а уравнение теплового баланса примет вид:
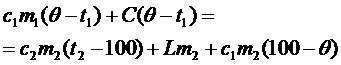 . .
|
| q-? | |

| 2. Если пар остынет от 120°С до 100°С, а сконденсируется не весь, то в калориметре будет находиться смесь воды и пара при температуре 100°С, а уравнение теплового баланса будет таким:
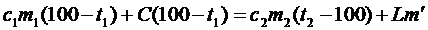 Здесь m¢- масса сконденсировавшегося пара.
Здесь m¢- масса сконденсировавшегося пара.
|
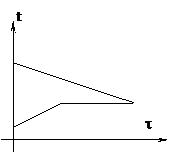
| 3. Пар может остыть от 120°С до 100°С, а вода и калориметр уже нагреются до 100°С, и при этом часть воды даже выкипит. В калориметре будет смесь пара и воды при температуре 100°С.
Уравнение теплового баланса будет иметь вид:
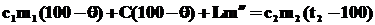 , где m¢¢- масса превратившейся в пар воды. , где m¢¢- масса превратившейся в пар воды.
|
| Каким из трёх уравнений пользоваться? Cделаем предварительные расчёты. Вычислим: а) сколько теплоты нужно для того, чтобы нагреть воду и калориметр от 25°С до 100°С: Q1 = c1m1(100 - t1) + C(100 - t1) = 4200×0,5×75+1200×75 = 247500 (Дж). б) сколько теплоты выделится, если весь пар остынет от 120°С до 100°С: Q2 = c2m2(t2 - 100) =2100×0,05×20 = 2100 (Дж). в) сколько теплоты выделится, если весь пар сконденсируется в воду при температуре 100°С: Q3 = Lm2 = 2300000×0,05 = 115000 (Дж). |
Выделяющаяся теплота Q2 + Q3 = 2100 Дж + 115000 Дж = 117100 Дж при охлаждении пара и его конденсации меньше теплоты, которая требуется для нагревания «холодной» воды и калориметра. Значит, чтобы вода вместе с калориметром смогла нагреться до 100°С, ей нужно больше энергии, чем может отдать пар, остывая и конденсируясь. Поэтому 117100 Дж пар отдаст, став при этом «горячей» водой при 100°С, а «холодная» вода при этом до 100°С ещё не нагреется. Тогда в калориметре будут одновременно находиться сконденсировавшаяся из пара вода при 100°С и подогретая «холодная» вода. В результате дальнейшего теплообмена «горячая» вода остынет, а «холодная» нагреется. И в итоге в калориметре будет вода, температура которой ниже 1000С, но выше 250С.
Уравнение теплового баланса будет иметь вид (1):
c1m1(q - t1) + C(q - t1) = c2m2(t2 - 100) + Lm2 + c1m2(100 - q), откуда
c1m1q - c1m1t1 + Сq - Сt1 = 117100 + c1m2×100 - c1m2q.
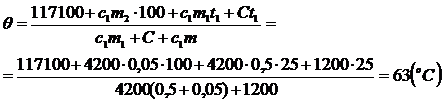
Ответ: В калориметре установится температура 63°С.

Задача 10
В калориметре находится вода массой 0,8 кг при температуре 20°С. В воду опустили 2 кг льда при температуре -30°С. Что будет в калориметре после того, как теплообмен прекратится? Теплоёмкостью калориметра пренебречь.
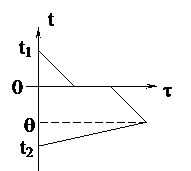 m1 = 0,8 кг
с1=4200 Дж/(кг×0С)
t1 = 20°С
m2 = 2 кг
t2 = -30°С
c2=2100 Дж/(кг×0С)
l = 3,4×105 Дж/кг m1 = 0,8 кг
с1=4200 Дж/(кг×0С)
t1 = 20°С
m2 = 2 кг
t2 = -30°С
c2=2100 Дж/(кг×0С)
l = 3,4×105 Дж/кг
| Решение Рассмотрим варианты решения: 1. Вода остынет от 20°С до 0°С, затем эта вода замёрзнет и станет льдом при температуре 0°С, затем лёд, образовавшийся из воды, остынет до температуры q (см. график). А опущенный в воду лёд только нагреется от температуры -30°С до температуры q. В калориметре будет находиться лёд при температуре q. Уравнение теплового баланса запишется так: c1m1(t1 - 0) + lm1 + c2m1(0 - q) = c2m2(q - t2). |
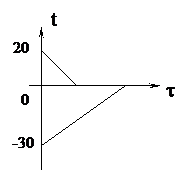 q, mв, mл –? q, mв, mл –?
|
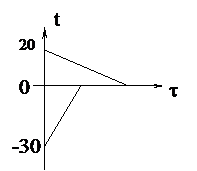 c1m1(t1 - 0) + lm¢ = c2m2(q - t2), где m¢ - масса превратившейся в лед воды.
c1m1(t1 - 0) + lm¢ = c2m2(q - t2), где m¢ - масса превратившейся в лед воды.
3. Вода остынет от 20°С до 0°С. Лёд при этом нагреется от -30°С до 0°С, затем частично или полностью расплавится и станет водой при 0°С. В калориметре будет смесь воды и льда при температуре 0°С. Уравнение теплового баланса запишется так:
c1m1(t1 - 0) = c2m2(0 - t2) + lm², где m² - масса превратившегося в воду льда.

 4. Лёд нагреется от -30°С до 0°С, расплавится, и образовавшаяся из льда вода нагреется от 0°С до температуры q. А вода массой m1 при этом остынет от 20°С до температуры q. Тогда в калориметре будет находиться вода при температуре q. Уравнение теплового баланса запишется так:
4. Лёд нагреется от -30°С до 0°С, расплавится, и образовавшаяся из льда вода нагреется от 0°С до температуры q. А вода массой m1 при этом остынет от 20°С до температуры q. Тогда в калориметре будет находиться вода при температуре q. Уравнение теплового баланса запишется так:
c1m1(t1 - q) = c2m2(0 - t2) + lm2 + c1m2(q - 0).
Проведем численный анализ ситуации. Сколько теплоты:
а) выделит вода при остывании от 20°С до 0°С:
Q1 = c1m1(t1 - 0) = 4200×0,8×20 = 67200 (Дж);
б) выделит вода при превращении в лед при 0°С:
Q2 = lm1 = 340000×0,8 = 272000 (Дж);
в) нужно получить льду, чтобы нагреться от -30°С до 0°С:
Q3 = c2m2(0 - t2) = 2100×2×30 = 126000 (Дж);
г) нужно получить льду, чтобы полностью расплавиться при температуре 0°С:
Q4 = lm2 = 340000×2 = 680000 (Дж).
Получаем: чтобы весь лёд нагрелся от -30°С до 0°С, ему нужно передать 126000 Дж теплоты, а вода при этом, остывая от 20°С до 0°С, может дать только 67200 Дж. Значит, лёд эти 67200 Дж у воды «возьмет», но ему ещё не будет хватать Q¢ = 126000 Дж - 67200 Дж = 58800 Дж, чтобы нагреться до 0°С. Он их «возьмёт» у превращающейся в лед воды (если бы вода полностью превратилась в лед, то она бы выделила 272000 Дж, а это больше, чем «нужно» льду):
Q¢ = lm¢ Þ m¢ = Q¢/l = 58800/340000 » 0,2 (кг), где
m¢ - это масса воды, обратившейся в лёд при температуре 0°С.
Как только лёд нагреется до 0°С, теплообмен между льдом и водой прекратится, так как они будут иметь одинаковые температуры.
Итак, получили: вода остынет до 0°С, часть её (а именно m¢ = 0,2 кг) замёрзнет и станет льдом при 0°С, а лёд нагреется до 0°С. И в результате в калориметре будет находиться смесь воды и льда при 0°С. При этом масса воды будет равна:
mв = m1 - m¢= 0,8 кг - 0,2 кг = 0,6 кг,
а масса льда равна: mл = m2 + m¢ = 2 кг + 0,2 кг = 2,2 кг.
Ответ: Вкалориметре при 0°С находится смесь воды (0,6 кг) и льда (2,2 кг).
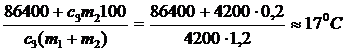 .
. m – m1 = m – m
m – m1 = m – m 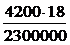 ) = 0,116 (кг) = 116 (г)
) = 0,116 (кг) = 116 (г)
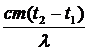 ;
;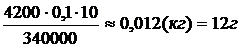 .
.