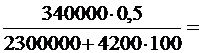1. Для приготовления ванны ёмкостью 100 л смешали холодную воду, имеющую температуру 12°С, и горячую, имеющую температуру 72°С. Сколько той и другой воды надо взять, чтобы температура воды в ванне была 36°С?*
2. Когда в 2 кг воды, находящейся в калориметре при 20°С, опустили алюминиевое тело массой 0,8 кг, имеющее температуру 100°С, температура воды поднялась до 25°С. Определить теплоёмкость калориметра.
3. В 2 кг воды, имеющей температуру 20°С, опустили сначала медное тело массой 2 кг, имеющее температуру 80°С. После того, как температура перестала меняться, в воду опустили железное тело массой 3 кг, имеющее температуру -20°С. Какой после этого стала температура воды? Теплоёмкостью сосуда пренебречь.
4. После опускания в воду, имеющую температуру 100°С, тела с температурой 20°С, установилась общая температура 80°С. Какой станет температура воды, если, не вынимая первого тела, в нее опустить ещё два таких же тела, имеющих температуру 20°С?
5. В чайник налили воду при температуре 200С и поставили на электроплитку. Через 13 минут вода закипела. Через какое время половина воды выкипит?
6. Для того, чтобы на спиртовом нагревателе, с КПД 70%, нагреть до кипения 1,4 кг воды и половину ее превратить в пар, израсходовали 100 г спирта. Какова начальная температура воды? Удельная теплота сгорания спирта 29×106 Дж/кг.
7. В калориметре находится лёд массой 500 г при температуре 0°С. В калориметр впускают водяной пар температурой 100°С. Сколько воды окажется в калориметре, когда весь лёд растает, а температура образовавшейся воды будет равна 0°С?
8. В калориметр, содержащий 400 г воды и 200 г льда при 0°С, впустили водяной пар с температурой 100°С. Сколько пара было впущено в калориметр, если в калориметре установилась температура 20°С? Теплоёмкость калориметра 1000 Дж/0С.
9. В сосуд теплоёмкостью 1000 Дж/0С, содержащий 5 кг воды при температуре 20°С, положили лёд, имеющий температуру -40°С. Температура образовавшейся смеси оказалась равна -2°С. Сколько льда было положено в сосуд?
10. В алюминиевом калориметре массой 200 г находится кусок льда с температурой -20°С. В калориметр впустили водяной пар, имеющий температуру 100°С. Когда температура калориметра стала равна 20°С, измерили массу его содержимого. Она оказалась равной 400 г. Найти массу льда, находящегося в калориметре, и массу сконденсировавшегося пара.
11. В калориметр, содержащий 3 кг воды при температуре 20°С, опустили 2 кг льда, имеющего температуру -10°С. Что будет в калориметре, когда теплообмен прекратится? Теплоемкостью калориметра пренебречь.
12. В калориметр, содержащий 1 кг льда и 800 г воды при 0°С впускают 100 г водяного пара при 100°С. Что будет в калориметре, когда теплообмен прекратится? Теплоемкостью калориметра пренебречь.
13. В калориметре находится вода массой 600 г при температуре 5°С. К ней долили ещё 300 г воды с температурой 10°С и положили 600 г льда с температурой -60°С. Что будет в калориметре после того, как теплообмен прекратится? Теплоемкостью калориметра пренебречь.
14. В теплоизолированном медном сосуде массой 400 г находятся 2 кг льда при температуре -10°С. В сосуд помещают 400 г водяного пара при температуре 110°С. Что будет в сосуде после того, как теплообмен прекратится?
15. В колбе находятся 200 г воды при температуре 0°С. Откачиванием паров всю воду в колбе заморозили. Сколько получилось льда?
Ответы и решения
1. 60 л холодной и 40 л горячей воды.
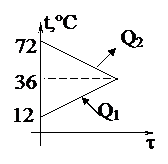 t1 = 12°С
t2 = 72°С
q = 36°С
V = 100 л t1 = 12°С
t2 = 72°С
q = 36°С
V = 100 л
| Решение Q1 = cm1(q - t1) – теплота, которую получит холодная вода, нагреваясь от 12°С до 36°С; Q2 = c(m - m1)(t2 - q) – теплота, которую отдаст горячая вода, остывая от 72°С до 36°С, |
| V1 -? V2 -? |
Q1 = Q2,
cm1(q - t1) = c(m - m1)(t2 - q),
m1(q - t1) + m1(t2 - q) = m(t2 - q),
rV1(q - t1 + t2 - q) = rV (t2 - q),
V1 = V× 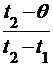 ;
;
V1 = 100× 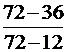 = 60 (л),
= 60 (л),
V2 = V - V1 = 100 – 60 = 40 (л).
2. 2640 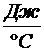 .
.
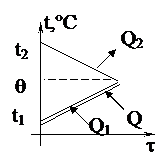 m1 = 2 кг
t1 = 20°С
с1=4200 Дж/(кг×0С)
m2 = 0,8 кг
t2 = 100°С
с2 = 920 Дж/(кг×0С)
q = 25°С _______
Ск -? m1 = 2 кг
t1 = 20°С
с1=4200 Дж/(кг×0С)
m2 = 0,8 кг
t2 = 100°С
с2 = 920 Дж/(кг×0С)
q = 25°С _______
Ск -?
| Решение
Q2 = Q + Q1, где
Q2 – теплота, отданная алюминиевым телом;
Q1 – теплота, полученная водой,
Q - теплота, полученная калориметром.
c2m2(t2 - q) = (Cк + c1m1)(q - t1),
Cк = 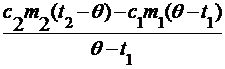 .
Cк = .
Cк = 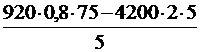 = 2640 (Дж/0С) = 2640 (Дж/0С)
|
3. 190С.
| m1 = 2 кг c1=4200 Дж/(кг×0С) t1 = 20°С m2 = 2 кг c2 = 380 Дж/(кг×0С) t2 = 80°С m3 = 3 кг c3 = 460 Дж/(кг×0С) t3 = -20°С | Решение
Здесь удобнее пользоваться уравнением теплового баланса в виде (6), так как при решении этим способом последовательность опускания в воду тел не важна:
Q1 + Q2 + Q3 = 0,
c1m1(q - t1) + c2m2(q - t2) + c3m3(q - t3) = 0,
q = 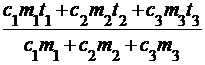 . .
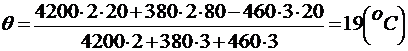
|
| q –? |
4. 53°С
| С1– теплоёмкость воды; t1 = 100°С С2– теплоёмкость тела; t2 = 20°С t3 = 80°С | Решение
1. При опускании в воду с температурой t1 первого тела:
С1(t1 - t3) = С2(t3 - t2). (1)
2. При опускании в воду с температурой t2 сразу трех тел:
С1(t1 - t4) = 3С2(t4 - t2). (2)
3. Делим уравнение (1) на уравнение (2) и получаем:
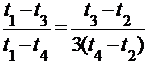 , ,
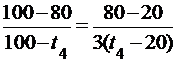 Решая это уравнение, находим, что: t4 » 53 °С.
Решая это уравнение, находим, что: t4 » 53 °С.
|
| t4 -? |
5. 44,5 мин.
| t1 = 13 мин t1 = 20°С t2 = 100°С m2 = m1/2 с = 4200 Дж/(кг×0С) L = 2,3×106 Дж/кг |
| t2 –? |
Решение
Мощность электроплитки подразумеваем постоянной. Поэтому:
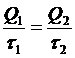 ,
,
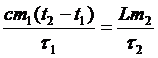 ,
,
откуда: 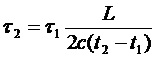 ,
,
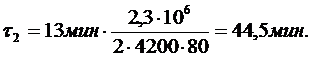
6. 29°С
 |
| m1 = 1,4 кг с1=4200 Дж/(кг×0С) t2 = 100°С h = 0,7 m2 = 0,1 кг q = 29×106 Дж/кг | Решение
h =  , где
Qполез = Q1 + Q2 =
= cm1(t2 - t1) + L , где
Qполез = Q1 + Q2 =
= cm1(t2 - t1) + L 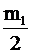 , а
Qзатр = qm2.
Тогда h = , а
Qзатр = qm2.
Тогда h = 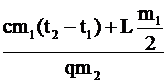
|
| t1-? |
Выражаем t1: t1 = t2 – 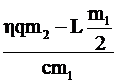
t1 = 100 - 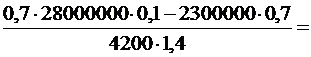 100 – 71 = 29 (°С).
100 – 71 = 29 (°С).
7. 563 г.
| m1 = 0,5кг l = 3,4×105 Дж/кг t1 = 0°С с = 4200 Дж/(кг×0С) L = 2,3×106 Дж/кг t2 = 100°С | 
Q1 = Q2 + Q3, lm1 = Lm2 + cm2(t2 - t1), m2 = m2 =
| ||
| m –? |
= 0,063 (кг) = 63 г
В итоге: m = m1 + m2 = 500 +63 = 563 (г).
8. 65 г
 m1 = 0,4 кг
m2 = 0,2 кг
l = 3,4×105 Дж/кг
t1 = 0°С
c =4200Дж/(кг×0С)
t2 = 100°С
L = 2,3×106 Дж/кг
q = 20°С
C = 1000 Дж/0С m1 = 0,4 кг
m2 = 0,2 кг
l = 3,4×105 Дж/кг
t1 = 0°С
c =4200Дж/(кг×0С)
t2 = 100°С
L = 2,3×106 Дж/кг
q = 20°С
C = 1000 Дж/0С
| Решение
Q1 + Q2 + Q3 = Q4 + Q5,
lm2 + c(m1 + m2)(0 - t1) +
+ C(q - t1) =
= Lm3 + cm3(t2 - q),
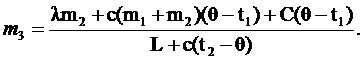 m3 =
m3 = 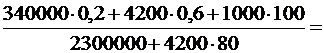 0,065 (кг). 0,065 (кг).
|
| m3 –? |
9. 27,1 кг.
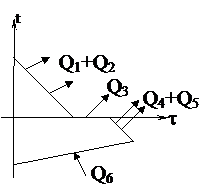 |
| C = 1000 Дж/0С m1 = 5 кг c1=4200 Дж/(кг×0С) t1 = 20°С t2 = -40°С c2=2100 Дж/(кг×0С) l = 3,4×105 Дж/кг q = -2°С | Решение Q1 + Q2 + Q3 + Q4 + Q5 = Q6, Q2 + Q4 = C(t1 - q) – теплота, отданная калориметром; Q1 + Q3 + Q5 = c1m1(t1 - 0) + lm1 + c2m1(0 - q) – теплота, отданная водой; Q6 = c2m2(q - t2) – теплота, принятая льдом. |
| m2 –? | |
Тогда m2 = 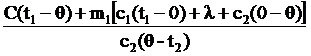 .
.
m2 = 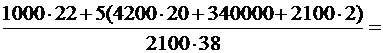 27,1 (кг).
27,1 (кг).
10. 340 г льда и 60 г пара.
 с1 = 920Дж/(кг×0С)
m1 = 0,2 кг
t1 = t2 = -20°С
c2=2100 Дж/(кг×0С)
t3 = 100°С
L = 2,3×106 Дж/кг
l = 3,4×105 Дж/кг
c3=4200 Дж/(кг×0С)
q = 20°С
m = 0,4 кг с1 = 920Дж/(кг×0С)
m1 = 0,2 кг
t1 = t2 = -20°С
c2=2100 Дж/(кг×0С)
t3 = 100°С
L = 2,3×106 Дж/кг
l = 3,4×105 Дж/кг
c3=4200 Дж/(кг×0С)
q = 20°С
m = 0,4 кг
| Решение Q1 + Q2 + Q3 + Q4 + Q5 = = Q6 + Q7. Q2, Q3, Q4 – теплоты, полученные льдом; Q1, Q5 – теплоты, полученные калориметром; Q6, Q7 – теплоты, отданные паром. c1m1(q - t1) + c2m2(0 - t2) + lm2 + c3m2(q - 0) = = L(m - m2) + c3(m - m2)(100 - q), Масса льда: |
| m2 –? m3 –? |
m2 = 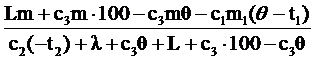
m2 = 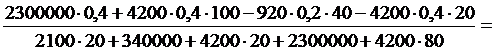 0,34 (кг)
0,34 (кг)
Масса пара: m3 = m – m2 = 0,4 кг – 0,34 кг = 0,06 кг.
11. Смесь, состоящая из 1,4 кг льда и 3,6 кг воды при температуре 00С.
| m1 = 3 кг t1 = 20°С c1= 4200 Дж/(кг×0С) m2 = 2 кг t2 = -10°С c2= 2100 Дж/(кг×0С) l = 3,4×105 Дж/кг | Решение 1. Q1 = c1m1(t1 - 0) = 4200×3×20 = 252000 (Дж) – может отдать вода, остывая от 20°С до 0°С. 2. Q2 = c2m2(0 - t2) = 2100×2×10 = 42000 (Дж) – нужно льду, чтобы нагреться от –10°С до 0°С. 3. Q3 = lm2 = 340000×2 = 680000 (Дж) – нужно льду, чтобы полностью расплавиться. 4. Q1 - Q2 < Q3 – значит, у воды не хватит энергии, чтобы расплавить весь лёд. |
| m¢1 –? m¢2 –? q –? |
Вывод: лёд растает не весь, и в калориметре будет находиться смесь воды со льдом при температуре 0°С.
Сколько растает льда?
lm¢ = Q1 - Q2 Þ m¢ = 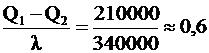 (кг)
(кг)
Тогда останется льда: m¢2 = m2 - m¢ = 2 кг – 0,6 кг = 1,4 кг.
Масса воды: m¢1 = m1 + m¢ = 3 кг + 0,6 кг = 3,6 кг
12. 0,2 кг льда и 1,7 кг воды при температуре 00С.
| m1 = 1 кг m2 = 0,8 кг t1 = t2 = 0°С l = 3,4×105 Дж/кг c = 4200 Дж/(кг×0С) m3 = 0,1 кг t3 = 100°С L = 2,3×106 Дж/кг | Решение 1. Q1 = lm1 = 340000×1 = 340000 (Дж) – нужно льду, чтобы полностью растаять при 00С. 2. Q2 = Lm3 = 2300000×0,1 = 230000 (Дж) – может отдать пар, конденсируясь при 1000С в воду. 3. Q3 = cm3(t3 - t1) = 4200×0,1×100 = 42000 (Дж) – может отдать пар, остывая от 1000С до 00С. 4. Q2 + Q3 = 230000 + 42000 = 272000 (Дж) < Q1. Поэтому лёд растает не весь, пар весь сконденсируется, а образовавшаяся из него вода остынет до 0°С. |
| q –? m¢1 –? m¢2 –? |
Сколько льда растает?
lm¢ = Q2 + Q3 Þ m¢ = 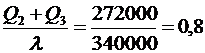 (кг).
(кг).
В калориметре останется льда: m¢1 = m1 - m¢ = 1 кг – 0,8 кг = 0,2 кг.
Масса воды: m¢2 = m2 + m¢ + m3 = (0,8 + 0,8 + 0,1) кг = 1,7 (кг)
Полученная смесь находится при температуре 0°С.
13. Смесь воды (750 г) и льда (750 г) при 00С.
| m1 = 0,6 кг c1= 4200 Дж/(кг×0С) t1 = 5°С m2 = 0,3 кг t2 = 10°С m3 = 0,6 кг t3 = -600С с2= 2100 Дж/(кг×0С) l = 3,4×105 Дж/кг | Решение 1. Q1 = c1m1(t1 - 0) = 4200×0,6×5 = 12600 (Дж) – выделят 600 г воды, остывая от 5°С до 0°С. 2. Q2 = c1m2(t2 - 0) = 4200×0,3×10 = 12600 (Дж) – выделят 300 г воды, остывая от 10°С до 0°С. Q1 + Q2 = 25200 Дж. 3. Q3 = c2m3(0 - t3) = 2100×0,6×60 = 75600 (Дж) – нужно льду, чтобы нагреться от -60°С до 0°С. Q3 > Q1 + Q2 Þ вся вода остынет до 0°С, а лёд ещё при этом не нагреется до 0°С. DQ = Q3 - (Q1 + Q2) = 75600 – 25200 = 50400 (Дж). Нагреваясь до 0°С, лед «приморозит» к себе часть воды m¢: |
| q –? mводы –? mльда –? |
lm¢ = DQ Þ m¢ = 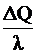 =
= 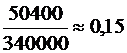 (кг).
(кг).
Итак, в калориметре будет находиться смесь воды со льдом при температуре 0°С:
mводы = m1 + m2 - m¢ = 0,6 + 0,3 - 0,15 = 0,75 (кг),
mльда = m3 + m¢ = 0,6 + 0,15 = 0,75 (кг)
14. 2,4 кг воды при температуре 360С.
| m1 = 0,4 кг c1 = 380 Дж/(кг×0С) m2 = 2 кг c2= 2100 Дж/(кг×0С) t1 = t2 = -10°С l = 3,4×105 Дж/кг m3 = 0,4 кг t3 = 110°С с3= 2100 Дж/(кг×0С) L = 2,3×106 Дж/кг c4= 4200 Дж/(кг×0С) | Решение 1. Q1 = c1m1(0 - t1) = 380×0,4×10 = 1520 (Дж) – нужно получить медному сосуду, чтобы нагреться от -10°С до 0°С. 2. Q2 = c2m2(0 - t1) = 2100×2×10 = 42000 (Дж) – нужно получить льду, чтобы он нагрелся от -10°С до 0°С. 3. Q3 = lm2 = 340000×2 = 680000 (Дж) – нужно получить льду, чтобы растаять и стать водой при 0°С. Q1 + Q2 + Q3 = 723520 (Дж) – нужно получить сосуду и льду, чтобы в сосуде при 0°С была вода. 4. Q4 = c3m3(t3 - 100) = 2100×0,4×10 = 8400 (Дж) – может отдать пар, остывая от 110°С до 100°С. 5. Q5 = Lm3 = 2300000×0,4 = 920000 (Дж) – может отдать пар, конденсируясь в воду при 1000С. |
| q –? m –? | |
Q4 + Q5 = 8400 + 920000 = 928400 (Дж) – может отдать пар, превращаясь в пар с температурой 100°С;
DQ = (Q4 + Q5) - (Q1 + Q2 + Q3) = 928400 – 723520 = 204880 (Дж) – столько энергии останется у пара, когда он станет водой при 1000С, (лед при этом превратится в воду при 0°С).
Проверим, хватит ли этой энергии, чтобы вода, образовавшаяся из льда, нагрелась вместе с сосудом от 0°С до 100°С?
Q6 = (c1m1 + c2m2)(100 - 0) = (380×0,4 + 4200×2)×100 = 855200 (Дж).
Это больше, чем 204880 Дж. Значит, вода, образовавшаяся из льда, нагреется не до 100°С. Найдем, до какой температуры нагреются вода и сосуд:
Q1 + Q2 + Q3 + (c1m1 + c4m2)(q - 0) = Q4 + Q5 + c4m3(100 - q),
c1m1q + c4m2q + c4m3q = c4m3×100 + 204880,
q = 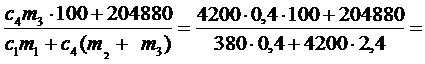 36(°С).
36(°С).
15. 174 г.
 m = 0,2 кг
l = 3,4×105 Дж/кг
L = 2,3×106 Дж/кг m = 0,2 кг
l = 3,4×105 Дж/кг
L = 2,3×106 Дж/кг
| Решение | |
|
Q1 = lm1 – энергия, которая выделяется при замерзании воды массой m1.
Q2 = L(m – m1) – энергия, которая необходима для превращения оставшейся воды в пар.
Q1 = Q2,
lm1 = L(m - m1)
m1 = m× 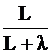 , откуда
, откуда
m1 = 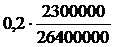 (кг) = 0,174 кг = 174 г.
(кг) = 0,174 кг = 174 г.
Учебное издание
Самарин Григорий Геннадьевич
Решение задач на теплообмен с использованием уравнения теплового баланса
(методические рекомендации)
Редактор – Г. Д. Попырина
Компьютерная верстка – К. В. Маренин
Подписано в печать:
Бумага типографская
Условных печатных листов – 2,25
Тираж – 100 экз.
Заказ –
Цена договорная.
Лицей естественных наук
610006, г. Киров, ул. Возрождения, 6
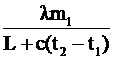 ,
,