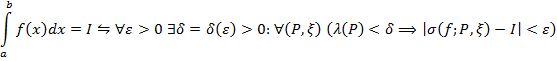
Замечание Можно доказать, что определение 5 равносильно тому, что

Определение 6 Функция 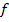 называется интегрируемой по Риману на сегменте
называется интегрируемой по Риману на сегменте  , если для неё определён интеграл Римана (т.е. если существует предел соответствующих интегральных сумм при
, если для неё определён интеграл Римана (т.е. если существует предел соответствующих интегральных сумм при 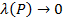 ).
).
Замечание Множество всех функций, интегрируемых по Риману на сегменте  обозначается через
обозначается через  .
.
Теорема 1 (линейность) Если  , то и линейная комбинация
, то и линейная комбинация 
 , причём
, причём

◄ Рассмотрим интегральную сумму, соответствующую интегралу, стоящему в левой части соотношения  , и преобразуем её:
, и преобразуем её:

или, что то же самое,
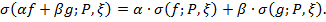
Поскольку существует предел при 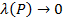 правой части данного равенства (так как в соответствии с условием
правой части данного равенства (так как в соответствии с условием  ), то существует также предел и левой его части. Таким образом, доказано, что
), то существует также предел и левой его части. Таким образом, доказано, что  . Поскольку эти пределы совпадают, доказано и равенство
. Поскольку эти пределы совпадают, доказано и равенство  . ►
. ►
Теорема 2 (монотонность) Если  ,
,  и
и  , то
, то

◄ При 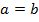 утверждение верно. Если
утверждение верно. Если  , рассмотрим соответствующее (очевидно верное) отношение интегральных сумм:
, рассмотрим соответствующее (очевидно верное) отношение интегральных сумм:

Переходя в данном неравенстве к пределу при 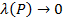 , существование которого гарантировано условием теоремы, доказываем проверяемое соотношение. ►
, существование которого гарантировано условием теоремы, доказываем проверяемое соотношение. ►
Теорема 3 (о среднем) Пусть  и функция
и функция  неотрицательна (или неположительна) на сегменте
неотрицательна (или неположительна) на сегменте  , тогда
, тогда 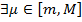 :
:


◄ Без ограничения общности доказательства положим  и
и  . Очевидна справедливость следующего двойного неравенства:
. Очевидна справедливость следующего двойного неравенства:

Поскольку в соответствии с теоремой об интегрируемости произведения интегрируемых функций (доказательство которой мы опустим)  ,
,  ,
,  , то применяя свойство линейности и монотонности интеграла, получаем
, то применяя свойство линейности и монотонности интеграла, получаем



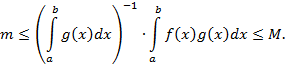
Обозначим число, стоящее в центре данного неравенства буквой  .
.


где  прямо по построению. ►
прямо по построению. ►
Следствие Если  (т.е. если
(т.е. если  непрерывна на сегменте
непрерывна на сегменте  ), то в силу теоремы о прохождении непрерывной на сегменте функции через любое промежуточное значение найдётся точка
), то в силу теоремы о прохождении непрерывной на сегменте функции через любое промежуточное значение найдётся точка  , такая, что
, такая, что

Теорема 4 (аддитивность) Пусть  и
и  , тогда
, тогда

◄ Рассмотрим такие разбиения сегмента  , в которых точка
, в которых точка  является точкой разбиения. Каждое такое размеченное разбиение
является точкой разбиения. Каждое такое размеченное разбиение  порождает разбиения
порождает разбиения  сегмента
сегмента  и
и  сегмента
сегмента  , причём
, причём  и
и  . В таком случае справедливо равенство
. В таком случае справедливо равенство

Так как  и
и  , то, переходя к пределу в данном равенстве при
, то, переходя к пределу в данном равенстве при  , получаем доказываемое равенство. ►
, получаем доказываемое равенство. ►
Замечание 1 Вообще говоря, нужно также доказать факт интегрируемости ограничения функции 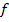 на сегменты
на сегменты  и
и  . Но это доказательство мы опустим.
. Но это доказательство мы опустим.
Замечание 2 Если точка  лежит вне сегмента
лежит вне сегмента  , то равенство
, то равенство  остаётся в силе. Пусть, например,
остаётся в силе. Пусть, например,  и
и 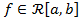 . И вправду, применяя формулу
. И вправду, применяя формулу  , получим
, получим
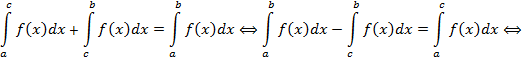
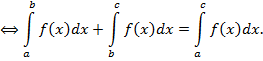
Теорема 5 (о существовании первообразной) Непрерывная на сегменте  функция
функция  имеет на этом сегменте первообразную, причём любая первообразная функции
имеет на этом сегменте первообразную, причём любая первообразная функции 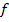 на
на  имеет вид
имеет вид

◄ Требуется доказать, что  , то есть
, то есть

Действительно,

где второе равенство верно в силу общепринятых договорённостей, последнее — в силу замечания 2 к теореме 4. Воспользовавшись формулой среднего значения (точнее, следствием из теоремы 3), продолжаем цепочку равенств
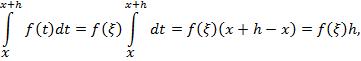
где  .
.
Следовательно,

где последнее равенство справедливо в силу непрерывности функции 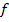 . ►
. ►
Замечание Прежде всего стоило обосновать существование интеграла в формуле  . Оказывается, это гарантируется теоремой об интегрируемости непрерывной функции, доказательство которой мы тоже опустим ввиду его сложности.
. Оказывается, это гарантируется теоремой об интегрируемости непрерывной функции, доказательство которой мы тоже опустим ввиду его сложности.
Следствие (формула Ньютона – Лейбница) Положим в  сначала
сначала  , а затем
, а затем  . Получим:
. Получим:  и
и
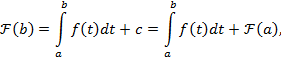
откуда незамедлительно получаем, что

