Трехфазный двухобмоточный трехстержневой трансформатор включен в сеть с напряжением UH при схеме соединения обмоток Y/Yн. Величины, характеризующие номинальный режим работы трансформатора, приведены в таблице 1: полная мощность SH, первичное линейное напряжение U1н; вторичное линейное напряжение U2н; напряжение короткого замыкания Uк; мощность потерь короткого замыкания (при номинальном токе) ркн. Кроме того, заданы значения тока холостого хода Iо (в % от I1н), мощность потерь холостого хода ро, коэффициент мощности cos φ2 и характер нагрузки.
Таблица 1 - Данные к задаче 1 раздела № 1
| Варианты | Sн, кВА | U1н, кВ | U2н, кВ | Uк, % | I0, % | р0, % | pкн, Вт | cos φ2 | Характер нагрузки |
| 0,4 | 4,5 | 3,2 | 0,9 | Активно-индуктивная | |||||
| 0,4 | 4,7 | 3,0 | 0,95 | Активно-индуктивная | |||||
| 0,4 | 4,7 | 2,8 | 0,85 | Активно-индуктивная | |||||
| 0,4 | 5,3 | 2,8 | 0,80 | Активно-индуктивная | |||||
| 0,4 | 4,7 | 2,6 | 0,70 | Активно-индуктивная | |||||
| 0,4 | 6,5 | 2,6 | 0,75 | Активно-емкостная | |||||
| 0,4 | 6,5 | 2,4 | 0,95 | Активно-индуктивная | |||||
| 0,4 | 6,8 | 2,4 | 1,0 | активная | |||||
| 0,4 | 6,5 | 2,3 | 0,9 | Активно-индуктивная | |||||
| 0,4 | 6,8 | 2,3 | 0,88 | Активно-индуктивная | |||||
| to | 0,4 | 4,5 | 2,1 | 0,8 | Активно-индуктивная | ||||
| 0,4 | 6,5 | 2,1 | 1,0 | активная | |||||
| 0,4 | 5,5 | 2,0 | 0,95 | Активно-емкостная | |||||
| 0,4 | 6,5 | 2,0 | 0,9 | Активно-емкостная | |||||
| 0,4 | 5,0 | 4,4 | 0,85 | Активно-индуктивная | |||||
| 0,4 | 6,6 | 4,0 | 0,80 | Активно-индуктивная | |||||
| 0,4 | 6,6 | 3,7 | 1,0 | активная | |||||
| 0,4 | 6,2 | 3,3 | 1,0 | активная | |||||
| 0,4 | 6,4 | 3,2 | 0,88 | Активно-индуктивная | |||||
| 0,4 | 5,5 | 1,4 | 0,82 | Активно-индуктивная | |||||
| 0,4 | 6,5 | 1,5 | 0,89 | Активно-емкостная | |||||
| 0,4 | 5,5 | 1,3 | 0,91 | Активно-индуктивная | |||||
| 0,4 | 6,5 | 1,4 | 0,81 | Активно-емкостная | |||||
| 0,4 | 6,5 | 1,0 | 0,78 | Активно-индуктивная | |||||
| 0,4 | 6,5 | 1,1 | 0,83 | Активно-емкостная | |||||
| 0,4 | 4,0 | 3,0 | 0,80 | Активно-индуктивная | |||||
| 0,4 | 4.5 | 3,0 | 0,90 | Активно-емкостная | |||||
| 0,4 | 4,5 | 2,8 | 0,80 | Активно-индуктивная | |||||
| 0,4 | 5,0 | 2,8 | 0,85 | Активно-емкостная | |||||
| 0,4 | 4,5 | 2,5 | 0,75 | Активно-индуктивная | |||||
| 0,4 | 6,5 | 2,5 | 0,85 | Активно-индуктивная | |||||
| 0,4 | 6,5 | 2,3 | 0,80 | Активно-емкостная | |||||
| 0,4 | 6,6 | 2,3 | 1,0 | активная | |||||
| 0,4 | 6,5 | 2,3 | 0,85 | Активно-индуктивная | |||||
| 0,4 | 6,6 | 2,3 | 0,85 | Активно-индуктивная | |||||
| 0,4 | 4,5 | 2,3 | 0,80 | Активно-емкостная | |||||
| 0,4 | 6,5 | 2,1 | 0,90 | Активно-индуктивная | |||||
| 0,4 | 5,5 | 2,0 | 0,90 | Активно-емкостная | |||||
| 0,4 | 6,5 | 2,0 | 0,85 | Активно-индуктивная | |||||
| 0,4 | 5,0 | 4,3 | 0,80 | Активно-индуктивная | |||||
| 0,4 | 6,5 | 4,0 | 0,85 | Активно-емкостная | |||||
| 0,4 | 6,5 | 3,6 | 1,0 | активная | |||||
| 0,4 | 6,1 | 3,4 | 0,82 | Активно-индуктивная | |||||
| 0,4 | 6,3 | 3,1 | 0,75 | Активно-индуктивная | |||||
| 0,4 | 5,2 | 1,5 | 0,80 | Активно-емкостная | |||||
| 0,4 | 6,4 | 1,5 | 0,85 | Активно-индуктивная | |||||
| 0,4 | 5,5 | 1,3 | 0,85 | Активно-индуктивная | |||||
| 0,4 | 6,5 | 1,4 | 0,80 | Активно-емкостная | |||||
| 0,4 | 5,5 | 1,0 | 0,85 | Активно-индуктивная | |||||
| 0,4 | 6,5 | 1,1 | 0,80 | Активно-емкостная |
Содержание задания
1 Начертить электромагнитную схему трехфазного трансформатора и определить номинальные токи в обмотках трансформатора I1ф и I2ф, фазное напряжение обмоток U1ф и U2ф, коэффициент трансформации фазных напряжений к и ток холостого хода I0 в амперах.
2 Определить параметры схемы замещения трансформатора R1, X1, R/2, Х/2, Ro, Xo.
3 Построить зависимость КПД трансформатора от нагрузки η = f(β) при
cos φ2 = const и определить оптимальную загрузку его по току βопт.
4 Построить зависимость изменения вторичного напряжения от изменения нагрузки ΔU = f(β) и внешнюю характеристику трансформатора U2 = f(β) при U1= const и cos φ2 = const.
Примечание. При решении задачи все характерные величины трехфазного трансформатора определяют для одной фазы.
Рекомендации для выполнения
К пункту 1. Начертить электромагнитную схему трехфазного двухобмоточного трехстержневого трансформатора со схемой соединения Y/Yн. Для силовых трехфазных трансформаторов можно считать, что мощность 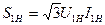 практически равна вторичной мощности
практически равна вторичной мощности 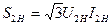 , поскольку номинальное значение КПД близко к единице. Поэтому номинальное (линейное) значение первичного и вторичного токов трансформатора следует определить из этих соотношений. Значения фазных токов и напряжений определяют на основе известных из курса ТОЭ соотношений между линейными и фазными величинами в трехфазной системе при соединении обмоток трансформатора в Y и Δ. Величину тока холостого хода в амперах определяют из соотношения
, поскольку номинальное значение КПД близко к единице. Поэтому номинальное (линейное) значение первичного и вторичного токов трансформатора следует определить из этих соотношений. Значения фазных токов и напряжений определяют на основе известных из курса ТОЭ соотношений между линейными и фазными величинами в трехфазной системе при соединении обмоток трансформатора в Y и Δ. Величину тока холостого хода в амперах определяют из соотношения
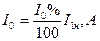 (1)
(1)
К пункту 2. Для определения параметров схемы замещения трансформатора вначале находят значение фазного напряжения короткого замыкания UКф, а также величину полного Zк, активного Rк и индуктивного Хк сопротивлений короткого замыкания по следующим зависимостям:
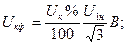
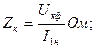 (2)
(2)
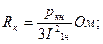
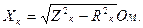 (3)
(3)
Поскольку Rк = R1 + R/2 и Хк = X1 + Х/2, то сопротивления обмоток трансформатора можно легко определить на основе допущения, что R1 ≈ R/2 и X1 ≈ Х/2, то есть R1 = R/2 = Rк/2 Ом и X1 = Х/2 = Хк/2 Ом.
Действительные значения сопротивлений вторичной обмотки трансформатора R2 и Х2 определяют из приведенных их значений R/2 и Х/2 и на основе соотношений
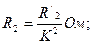 и
и 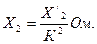 (4)
(4)
Значение величины полного Zm, активного Rm и индуктивного сопротивлений ветви намагничивания Хm для схемы замещения трансформатора определяют из соотношений
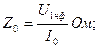
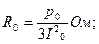
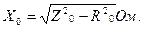 (5)
(5)
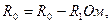
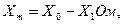


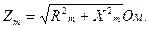 (6)
(6)
На основании выполненных расчетов следует вычертить Т-образную схему замещения трансформатора и указать на ней величины соответствующих сопротивлений.
К пункту 3. Оптимальный коэффициент загрузки трансформатора по току, соответствующий максимальному значению КПД, определяют из соотношения
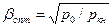 (7)
(7)
Величину КПД трансформатора при заданном значении загрузки по току βi = Ii/Iн определяют методом отдельных потерь по формуле
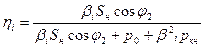 (8)
(8)
Для построения зависимости η = f(β) при U1 = const и cos φ2 = const в выражение (8) последовательно подставляют значения βi = 0; 0,25; 0,5; 0,75; 1,0; 1,25 и βопт и находят соответствующие им значения ηi. Для упрощения вычислений можно воспользоваться современными средствами автоматизации расчетов.
К пункту 4. Для построения зависимости η = f(β)) при U1 = const и cos φ2 = const пользуются выражением
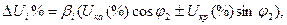 (9)
(9)
где Uка, Uкр соответственно значения падения напряжения на активном и индуктивном сопротивлении короткого замыкания трансформатора, которые определяют из соотношений
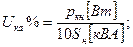
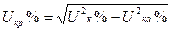 (10)
(10)
В выражение (9) подставляют значения βi = 0; 0,25; 0,50; 0,75; 1,0; 1,25 и находят соответствующие им значения ΔU1. На основании данных расчетов строят график ΔU1 = f(β).
Для построения внешней характеристики трансформатора U2 = f(β) при U1 = const и cos φ2 = const находят значение величины вторичного напряжения U2 с учетом характера нагрузки (столбец 10) при рассматриваемых выше значениях βi, т. е. U2i = U2н% - ΔUi, %. На основании полученных данных строят график U2 = f(β).