Под оптимизацией понимают процесс выбора наилучшего варианта из всех возможных. С точки зрения инженерных расчетов методы оптимизации позволяют выбрать наилучший вариант конструкции, наилучшее распределение ресурсов, минимальный урон природной среде и т. п. В процессе решения задачи оптимизации необходимо найти оптимальные значения некоторых параметров, их называют проектными параметрами. Выбор оптимального решения проводится с помощью некоторой функции, называемой целевой функцией. Целевую функцию можно записать в виде
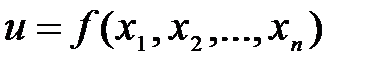, (10)
где х1,х2,...,хп- проектные параметры.
Можно выделить 2 типа задач оптимизации - безусловные и условные. Безусловная задача оптимизации состоит в отыскании максимума или минимума функции (10) от п действительных переменных и определении соответствующих значений аргументов на некотором множестве G n-мерного пространства. Обычно рассматриваются задачи минимизации; к ним легко сводятся и задачи на поиск максимума путем замены знака целевой функции на противоположный. Условные задачи оптимизации - это такие, при формулировке которых задаются некоторые условия (ограничения) на множестве G. Здесь рассмотрим только безусловные задачи оптимизации.
Поиск минимума функции одной переменной.
Для решения этой задачи используются методы золотого сечения или параболической интерполяции (в зависимости от формы задания функции), реализованные в программе fminbnd.
Пример 8. Найти и вывести на печать минимальное значение функции
f(x) = 24 - 2х /3 + х2/ 30 на [5; 20].
Строим график этой функции, чтобы убедиться в наличии минимума на заданном интервале.
Протокол программы
>> х = 5.0: 0.001: 20.0; у = 24 - 2* х/3 + х. ^2/30;
>> plot(x, у); grid on
Появляется окно с графиком этой функции (рис. 5), где отмечаем наличие минимума.
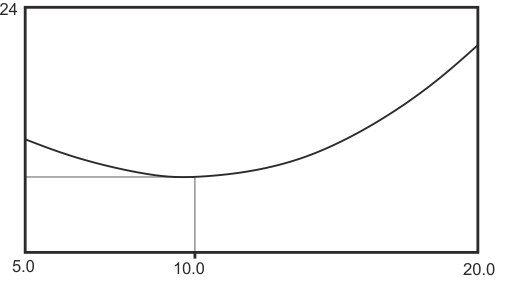
Рис. 5 – График функции f(x) = 24 - 2х /3 + х2/ 30
Далее, для точного определения координаты и значения минимума привлекаем программу fminbnd.
>> [х, у] = fminbnd ( ' (24.0 - 2* х/3 + х.^2/30) 5.0, 20.0)
Результат поиска
х =
10.0000
y =
20.6667
Варианты заданий. Найти и вывести на печать координату и минимальное значение функции f(x) на [а; b]. Данные взять из таблицы 8.
Таблица 8
| № п/п | Функция f(х) | Отрезок [a; b] |
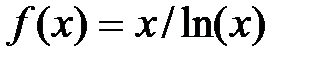
| [1.2; 4] | |
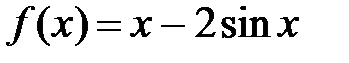
| [0; π/2] | |
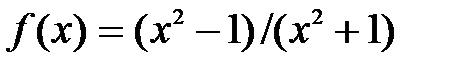
| [-2; 2] | |
| [-2; 2] | |
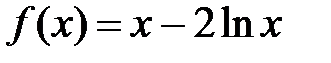
| [1; 3] | |
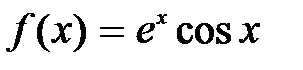
| [π; 3π/2] | |
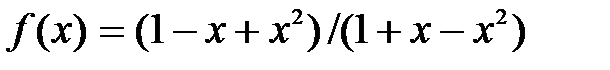
| [0; 1] | |
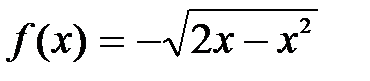
| [0; 2] | |
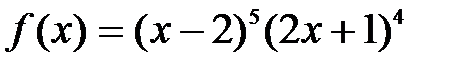
| [-0.5; 1.5] | |
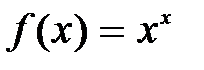
| [0,1; 1.0] | |
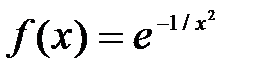
| [-0.5; 0,5] | |
| [-1.0; 0] | |
| [-0.5; 0.5] | |
| [0.5; 1.5] | |
| [1.6; 2.2] | |
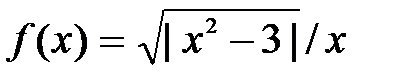
| [i; 2] | |
| [i.i; 1.6] | |
| [0; 7i/3] | |
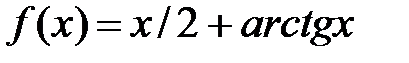
| [0.5; 1.2] | |
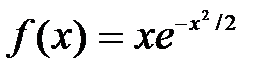
| [-1.5;-0.5] | |
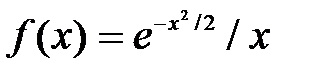
| [-2.0;-1.0] | |
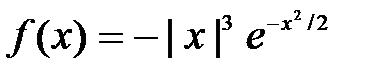
| [-2.0;-1.0] | |
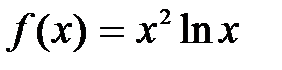
| [0.1; 1.0] | |
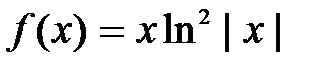
| [-0,05; -0.2] | |
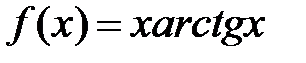
| [-0.5; 0.5] | |
| [π; 3π/2] | |
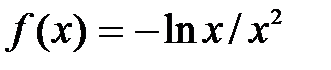
| [1.0; 2.0] | |
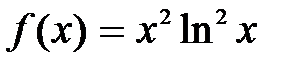
| [0.1; 0.5] | |
| [π; 2π] | |
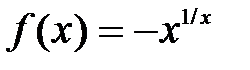
| [2.0; 3.0] |
6. Поиск минимума функций нескольких переменных
Данная задача значительно сложнее первой. Рассмотрим ее решение на примере функции двух переменных. Алгоритм может быть распространен на функции большего числа переменных. Для минимизации функций нескольких переменных MATLAB использует симплекс - метод Нелдера-Мида. Данный метод является одним из лучших методов поиска минимума функций многих переменных, где не вычисляются производные или градиент функции. Он сводится к построению симплекса в n-мерном пространстве, заданного п + 1 вершиной. В двухмерном пространстве симплекс является треугольником, а в трехмерном - пирамидой. На каждом шаге итераций выбирается новая точка решения внутри или вблизи симплекса. Она сравнивается с одной из вершин симплекса. Ближайшая к этой точке вершина симплекса заменяется этой точкой. Таким образом, симплекс перестраивается и позволяет найти новое, более точное положение точки решения. Алгоритм поиска повторяется, пока размеры симплекса по всем переменным не станет меньше заданной погрешности решения. Программу, реализующую симплекс-методы Нелдера-Мида, удобно использовать в следующей записи
[ х, min f ] = fmin search (...)
где х - вектор координат локального минимума;
minf - значение целевой функции в точке минимума.
Саму целевую функцию удобно представить с помощью дескриптора @ в М-файле.
Пример 9. Найти и вывести на печать координаты и значение минимума
функции двух переменных f(х, у) = (х2 + у2 - 3)2 + (х2 + у2 - 2х - 3)2 +1, если начальная точка поиска имеет координаты М0 (1; 1). Анализ функции показывает, что min f= 1 х = 0, у =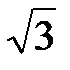 
=1.73205.
Строим трехмерный график этой функции, чтобы убедиться в наличии минимума. Возьмем интервал х ϵ [-1; 1] ;у ϵ [1;3].
Протокол программы
>> [X,Y] = mesh grid ([-1: 1, 1: 3]);
>> Z = (Х.^2 + Y.^2 - 3).^2 + (Х.^2 + Y.^2 - 2*X - 3).^2 + 1;
>> plot 3 (X,Y,Z)
После построения трехмерного графика выполняем поиск минимума. В М-файле программируем целевую функцию
Function = F ху(х)
f= (х (1)^2 + х (2)^2 -3)^2 - 3)^2 + (х (1)^2 + х (2)^ 2 -2* х(1) - 3)^2 + 1;
Решаем поставленную задачу в окне команд
>> [xmin, minf] =fminsearch (@ F ху, [1; 1])
Результаты поиска
xmin =
-0.0000 1.7320
minf =
1.0000
Как видно, результаты решения задачи точные.
Варианты заданий. Найти и вывести на печать координаты и минимальное значение функции двух переменных. Поиск начать с точки М0 (x0, y0). Данные взять из таблицы 9.
Таблица 9
| № п/п | Функция f(x, у) | Координаты начальной точки М0 (х0, y0). |
| (2 х 2 - у - 3)2 + х2 + 2х + 2 | (1; 1) | |
| (ху + 2)2 + у2 + 2у + 4 | (2; 2) | |
| (х2у2 - у + 2)2 + х2 +1 | (2; 2) | |
| (3 х 2 + 2у2 - 1)2 + (ху - 3)2 | (2; 2) | |
| (2 х 2 - 7у2 - 2)2+ (х 2 +у2 - 20)2 + 3 | (2; 2) | |
| (х 2 + у2 - 2 х - 3)2 + (х 2 + у2 -2у- 3)2 | (2; 2) | |
| (х 2 -6х + у2 + 8)2 + х 2 у 2 +1 | (2; 2) | |
| (х 2 - у - 2)2 + (х - у + 3)2 | (2; 2) | |
| ln(l + x 2 + у 2)2 +(x - y -l)2 | (2; 2) | |
| (х 2 + у2 - l)2 + (х 2 - 6 х + у 2 + 8)2 | (2; 2) | |
| х3 +у3 -3 ху | (0.5; 0.5) | |
| x2 + ху + у2 - 3 x - 6 у | (0.5; 3.5) | |
| -xy2(l-x-y) | (0; 0) | |
| 3 х 2 - х 3 + 3 у2 + 4 у | (0.1;-1.0) | |
| ху + 50/х + 20/у | (4;1) | |
| х 2 + у2 -2ln х -18ln y | (0.5; 2.5) | |
| х 3 +3 ху 2 -15 х -12 у | (1.5; 0.5) | |
| 2 х 3 - ху2 + 5х2 + у2 | (0.5; 0.5) | |
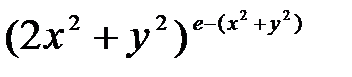
| (0.3; 0.3) | |
| (0.25; 0.25) | |
| (х -1)2 + (у - 1)2 - 1 | (0.5; 1.5) | |
| sin(x 2 + у2 - 0.5) | (0.5; 0.5) | |
| х 2 - ху + у2 + 2х - 2у + 1 | (-1.5; 0.5) | |
| xу (x+y - 4) | (1.0; 1.0) | |
| х3у2(х+у- 5 ) | (2.0; 1.5) | |
| х2 + ху+у2 +1/ х + 1/ у | (0.2; 0.3) | |
| -(sin х +sin у + sin(x + у)) | (π/4; π/4 ) | |
| -sin х· sin у· sin(x + у) | (π/4; п/4 ) | |
| х3у3-9 ху +1 | (2.5; 2.5) | |
| х 4+ у 4 -2х2+4ху-2у2+ 1 | (1.0;-1.0) |
В заключение отметим, что представленные примеры использования возможностей MATLAB в решении различных научно-технических проблем являются лишь небольшой иллюстрацией значительно большего потенциала системы, а материал главы может служить некоторым введением при самостоятельном изучении и применении интегрированного пакета математического моделирования.