Определение последовательности
Если каждому натуральному числу 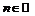 сопоставлено вещественное число
сопоставлено вещественное число 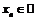 , то говорят, что задана числовая последовательность
, то говорят, что задана числовая последовательность  .
.
Последовательность может быть задана с помощью формулы: 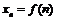 ,
, 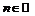 (данная формула называется формулой общего члена последовательности), а также через рекуррентные формулы, т.е. формулы, выражающие
(данная формула называется формулой общего члена последовательности), а также через рекуррентные формулы, т.е. формулы, выражающие 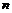 - член последовательности через члены с меньшими номерами (известными примерами здесь являются арифметическая и геометрическая прогрессии).
- член последовательности через члены с меньшими номерами (известными примерами здесь являются арифметическая и геометрическая прогрессии).
Примеры последовательностей:
1) 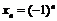 - множество значений последовательности состоит из двух чисел 1 и –1.
- множество значений последовательности состоит из двух чисел 1 и –1.
2) 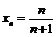 - множество значений последовательности бесконечно.
- множество значений последовательности бесконечно.
3) 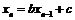 ,
, 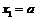 ,
, 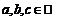 - заданные числа.
- заданные числа.
4) 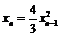 ,
, 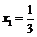 .
.
Последовательность может быть задана и другими способами, например, 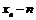 -я цифра в десятичной записи числа
-я цифра в десятичной записи числа 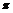 :
: 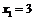 ,
, 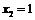 ,
, 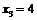 ,...
,...
Определение предела последовательности
Число 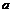 называется пределом последовательности
называется пределом последовательности  , если для
, если для 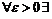 натуральное число
натуральное число 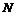 такое, что для
такое, что для 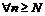 имеет место неравенство
имеет место неравенство 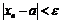 :
:
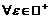
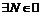
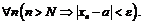
Для предела используется следующее обозначение 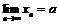 , либо
, либо 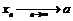 .
.
Неравенство 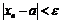 равносильно
равносильно 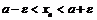 , и тогда легко дать геометрическое истолкование предела последовательности: в любой
, и тогда легко дать геометрическое истолкование предела последовательности: в любой 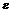 - окрестности точки
- окрестности точки 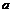 содержится бесконечно много членов последовательности
содержится бесконечно много членов последовательности  с номерами, большими
с номерами, большими 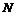 , а вне этой окрестности – лишь конечное число членов.
, а вне этой окрестности – лишь конечное число членов.
Если последовательность  имеет предел, то говорят, что последовательность сходится.
имеет предел, то говорят, что последовательность сходится.
Теорема о единственности предела последовательности
Если последовательность имеет предел, то этот предел единственный.
Пример 1.Доказать, опираясь на определение, что 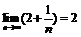 .
.
Рассмотрим модуль разности: 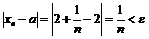 , т.е. при
, т.е. при 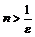 неравенство
неравенство 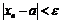 будет выполнено. Поэтому в качестве номера
будет выполнено. Поэтому в качестве номера 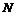 можно взять любое натуральное число, удовлетворяющее условию
можно взять любое натуральное число, удовлетворяющее условию 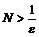 , например
, например 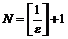 .
.
|
|
Из данного примера следует, что номер 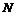 не может быть указан раз и навсегда, вообще говоря, он зависит от выбора числа
не может быть указан раз и навсегда, вообще говоря, он зависит от выбора числа 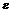 . И при его уменьшении соответствующий номер
. И при его уменьшении соответствующий номер 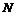 увеличивается.
увеличивается.
Пример 2.Доказать, исходя из определения, что 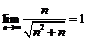 .
.
Рассмотрим модуль разности:
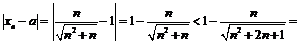
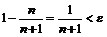 , откуда
, откуда 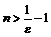 . Следовательно, в качестве
. Следовательно, в качестве 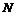 можно выбрать
можно выбрать 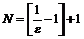 . Тогда для
. Тогда для 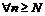 имеет место
имеет место 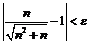 . Заметим, что в данном примере, как и во многих других, мы не решали неравенство
. Заметим, что в данном примере, как и во многих других, мы не решали неравенство 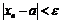 , т.е. не находили те и только те значения
, т.е. не находили те и только те значения 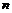 , для которых оно выполняется. Нам лишь необходимо определить тот номер
, для которых оно выполняется. Нам лишь необходимо определить тот номер 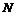 , начиная с которого все члены последовательности
, начиная с которого все члены последовательности  лежат в
лежат в 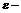 окрестности числа
окрестности числа 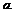 Будет ли это неравенство выполняться для номеров
Будет ли это неравенство выполняться для номеров 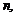 меньших
меньших 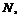 или нет, нас не интересует. Таким образом, в рассмотренном примере мы указываем номер
или нет, нас не интересует. Таким образом, в рассмотренном примере мы указываем номер 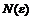 «с запасом», используя приём усиления неравенства и разрешая относительно
«с запасом», используя приём усиления неравенства и разрешая относительно 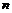 более простое неравенство:
более простое неравенство: 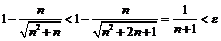 .
.
Сформулируем отрицание определения предела последовательности: «число 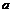 не является пределом последовательности
не является пределом последовательности  » в позитивном смысле (позитивное – значит утверждающее наличие каких-то свойств, а не отсутствие чего-либо, поэтому не содержащее слов «не», «нет», и т.д.).
» в позитивном смысле (позитивное – значит утверждающее наличие каких-то свойств, а не отсутствие чего-либо, поэтому не содержащее слов «не», «нет», и т.д.).
Число 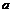 не является пределом последовательности
не является пределом последовательности 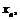 если
если 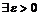 такое, что для любого натурального числа
такое, что для любого натурального числа 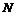 найдётся
найдётся 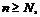 что будет выполнено неравенство:
что будет выполнено неравенство: 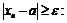
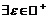
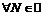
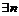
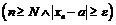
Геометрически это означает, что существует окрестность числа 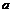 , вне которой находится бесконечно много членов последовательности
, вне которой находится бесконечно много членов последовательности 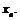
Пример 3. Доказать, что 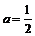 не является пределом последовательности
не является пределом последовательности 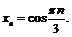
Выпишем несколько членов нашей последовательности:
|
|
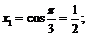
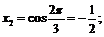
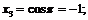
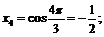
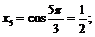
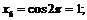 и т. д.
и т. д.
Пусть 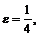 тогда какой бы ни был номер
тогда какой бы ни был номер 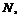
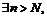 например,
например, 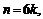 где
где 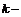 натуральное число
натуральное число 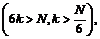 что будет иметь место неравенство:
что будет иметь место неравенство: 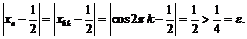
Мы могли бы выбрать другое 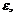 например,
например, 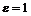 и для
и для 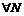 указать
указать 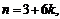 тогда
тогда 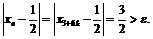
Последовательность называется расходящейся, если никакое число не является пределом этой последовательности, т.е.
для 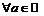
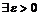
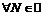
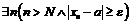 .
. 
Пример 4. Доказать, что последовательность 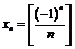 расходится.
расходится.
Если 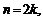 то
то 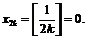 Если же
Если же 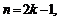 то
то  Пусть
Пусть 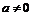 и
и 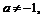 тогда
тогда 
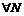
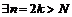 , что
, что 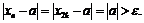
Если же 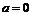 или
или 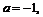 то можно положить
то можно положить 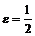 , и тогда вне
, и тогда вне 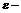 окрестности числа
окрестности числа 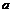 окажутся все (т.е. бесконечно много) члены последовательности с нечетными номерами (для
окажутся все (т.е. бесконечно много) члены последовательности с нечетными номерами (для 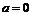 ) или все члены последовательности с чётными номерами (для
) или все члены последовательности с чётными номерами (для 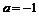 ).
).
Следовательно, последовательность 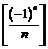 расходящаяся.
расходящаяся.
Пример 5. Пусть в некоторой 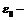 окрестности точки
окрестности точки 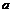 лежит бесконечно много членов последовательности
лежит бесконечно много членов последовательности  . Следует ли из этого условия, что: а)
. Следует ли из этого условия, что: а) 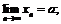 б) никакая точка
б) никакая точка 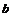 вне этой окрестности не является пределом последовательности
вне этой окрестности не является пределом последовательности 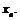
а) Не следует, так как предыдущий пример показывает, что в окрестности точки 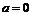 лежат бесконечно много членов последовательности
лежат бесконечно много членов последовательности 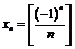 , но эта последовательность расходится.
, но эта последовательность расходится.
б) Следует, ибо можно указать 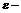 окрестность точки
окрестность точки 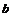 , вне которой содержится бесконечно много членов нашей последовательности. Для этого достаточно взять
, вне которой содержится бесконечно много членов нашей последовательности. Для этого достаточно взять 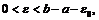 если
если 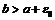 или
или 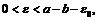 если
если 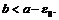
Пример 6. Пусть задана последовательности  . Определим последовательность
. Определим последовательность 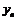 путём сдвига:
путём сдвига: 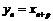 (либо
(либо 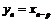 ,
, 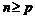 ). Доказать, что если существует
). Доказать, что если существует 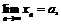 то существует и
то существует и 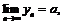 если же последовательность
если же последовательность  расходится, то последовательность
расходится, то последовательность 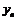 также расходится.
также расходится.
Рассмотрим сначала сходящуюся последовательность  . Это означает, что для
. Это означает, что для 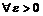
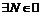 такое, что для
такое, что для 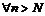 имеет место неравенство:
имеет место неравенство: 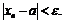 Но тогда в силу равенства
Но тогда в силу равенства 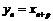 (либо
(либо 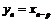 ) для
) для 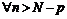
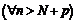 будет выполняться неравенство:
будет выполняться неравенство: 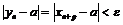
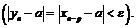 Согласно определению последовательность
Согласно определению последовательность 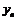 сходится к числу
сходится к числу 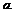
|
|
Пусть теперь  расходится, т.е. для
расходится, т.е. для 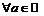
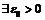 такое, что для
такое, что для 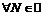
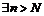 и такое, что
и такое, что 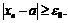 Взяв
Взяв 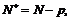 найдём
найдём 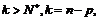 что
что 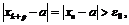 ведь
ведь 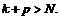
Следовательно, для 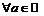
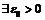 такое, что для
такое, что для 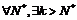 , и тогда
, и тогда 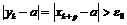 , что означает расходимость последовательности
, что означает расходимость последовательности 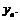
Итак, доказана следующая теорема:
Отбрасывание или добавление конечного числа членов последовательности не влияет на её сходимость.
Теорема об ограниченности сходящейся последовательности
Если последовательность имеет предел, то она ограничена.
Ограниченность последовательности – необходимое условие её сходимости, т.е. если последовательность не ограничена, то она расходится.
Пример 7. Доказать, пользуясь теоремой об ограниченности сходящейся последовательности, что последовательность 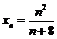 расходится.
расходится.
Покажем, что данная последовательность не ограничена, т.е. для 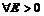
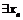 такое, что
такое, что 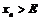 .
.
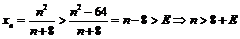 .
.
Итак, для любого 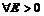
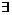 натуральное число
натуральное число 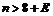 , при котором имеет место
, при котором имеет место 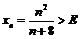 .
.
Определение бесконечно малой последовательности
Последовательность 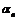 называется бесконечно малой, если
называется бесконечно малой, если 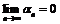 .
.
Пример 8. Доказать, что 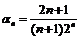 – бесконечно малая последовательность.
– бесконечно малая последовательность.
Согласно определению требуется доказать, что 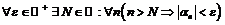 .
.
Рассмотрим 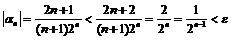 .
.
Откуда, логарифмируя, получим: 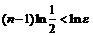 ,
, 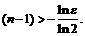 Итак,
Итак, 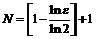 .
.
Последовательность  ограничена, если существуют числа
ограничена, если существуют числа 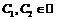 такие, что
такие, что 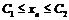 .
.
Леммы о бесконечно малых последовательностях.
Лемма 1. Если последовательности 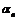 и
и 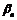 – бесконечно малые, а
– бесконечно малые, а 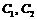 – вещественные числа, то последовательность
– вещественные числа, то последовательность 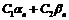 также бесконечно малая.
также бесконечно малая.
Лемма 2. Если последовательность 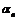 – бесконечно малая, а последовательность
– бесконечно малая, а последовательность  – ограниченная, то произведение
– ограниченная, то произведение 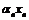 – бесконечно малая последовательность.
– бесконечно малая последовательность.
Пример 9. Используя лемму о бесконечно малых, доказать, что 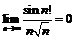 .
.
Последовательность 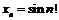 является ограниченной:
является ограниченной:  , а последовательность
, а последовательность 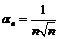 – бесконечно малая, так как
– бесконечно малая, так как 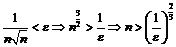 , т.е. для
, т.е. для 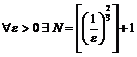 такое, что для
такое, что для 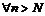 имеет место неравенство:
имеет место неравенство: 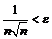 .
.
Следовательно, последовательность 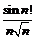 – бесконечно малая.
– бесконечно малая.
Пример 10. Доказать: 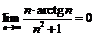 .
.
Последовательность 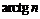 ограничена:
ограничена: 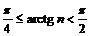 , а
, а 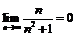 , так как
, так как 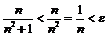 . Следовательно, их произведение есть бесконечно малая, т.е.
. Следовательно, их произведение есть бесконечно малая, т.е. 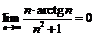 .
.
Определение бесконечно большой последовательности Последовательность  называется бесконечно большой, если для
называется бесконечно большой, если для 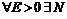 такое, что для
такое, что для 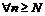 имеет место неравенство
имеет место неравенство 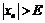 :
:
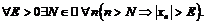
В этом случае пишут: 
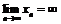 . Очевидно, что бесконечно большая последовательность является расходящейся.
. Очевидно, что бесконечно большая последовательность является расходящейся.
Пример 11.Доказать, что 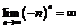 . Рассмотрим
. Рассмотрим 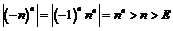 , если
, если 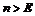 , т.е.
, т.е. 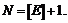
Пример 12.Доказать, что 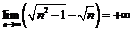 . Требуется для
. Требуется для 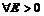 указать номер
указать номер 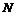 такой, что для
такой, что для 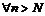 выполняется
выполняется 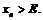
Рассмотрим
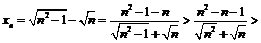
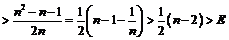 .
.
Следовательно, неравенство 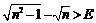 будет выполнено, если
будет выполнено, если 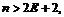 т.е.
т.е. 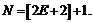
Пример 13. Доказать, что последовательность 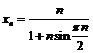 не ограничена, но не является бесконечно большой.
не ограничена, но не является бесконечно большой.
Сформулируем в положительном смысле утверждение: “последовательность не является бесконечно большой“:
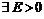
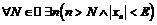 .
.
С другой стороны, требуется доказать неограниченность последовательности 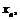 т.е.
т.е. 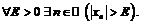
Выпишем первые несколько членов нашей последовательности:
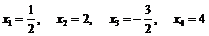 ,
,
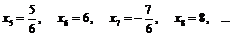
Итак, для 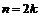
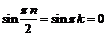 , поэтому
, поэтому 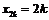 ;
;
для 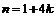
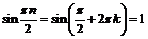 , откуда
, откуда 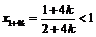 .
.
Следовательно, какое бы число 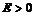 мы не выбрали,
мы не выбрали, 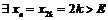 , если
, если 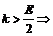 последовательность
последовательность  не ограничена. В то же время
не ограничена. В то же время 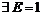 , что какое бы натуральное
, что какое бы натуральное 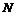 мы не взяли, можно указать
мы не взяли, можно указать 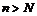 и равное при этом
и равное при этом 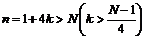 , что имеет место
, что имеет место 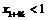 - последовательность
- последовательность  не является бесконечно большой.
не является бесконечно большой.
Связь бесконечно большой последовательности с бесконечно малой
Если  - бесконечно большая последовательность, то
- бесконечно большая последовательность, то 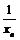 – бесконечно малая и наоборот, если
– бесконечно малая и наоборот, если  - бесконечно малая, то
- бесконечно малая, то 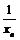 – бесконечно большая.
– бесконечно большая.
Пример 14. Доказать, что 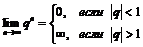 .
.
Рассмотрим неравенство: 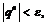 если
если 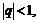 логарифмируя, будем иметь:
логарифмируя, будем иметь: 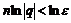 , откуда
, откуда 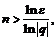 т.к.
т.к. 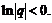 Следовательно, для
Следовательно, для 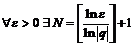 , что для всех
, что для всех 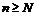 выполняется
выполняется 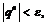 если
если 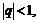 т.е.
т.е. 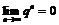 для
для 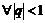 .
.
Пусть теперь 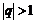 , тогда
, тогда 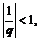 т.е., по доказанному выше, последовательность
т.е., по доказанному выше, последовательность 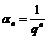 является бесконечно малой, откуда следует, что последовательность
является бесконечно малой, откуда следует, что последовательность 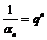 бесконечно большая при
бесконечно большая при 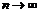 .
.
Теорема об арифметических свойствах предела
Если существуют 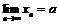 и
и 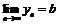 , то
, то
существует 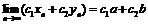 - для
- для 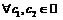 ;
;
существует 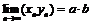 ; в случае
; в случае 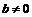 существует
существует 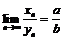 .
.
Пример 15. Найти 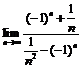 .
.
В данном примере невозможно непосредственно воспользоваться теоремой о пределе частного, так как не существует 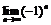 (
(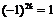 ,
, 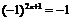 и вне
и вне 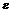 – окрестности, где
– окрестности, где 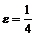 - например, любого числа
- например, любого числа 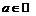 находится бесконечно много членов данной последовательности). Поэтому необходимо провести следующее преобразование:
находится бесконечно много членов данной последовательности). Поэтому необходимо провести следующее преобразование:

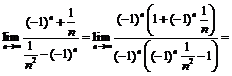

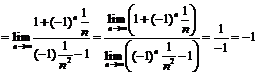 .
.
Пример 16. Найти 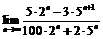 .
.
Учитывая, что 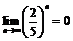 , получим:
, получим:
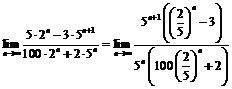
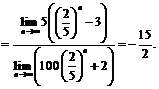
Пример 17. Найти 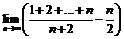 .
.
Сумма n членов арифметической прогрессии равна:
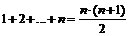 .
.
Тогда 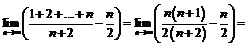
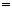
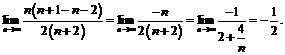
Пример 18. Найти 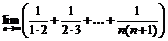 .
.
Учитывая, что 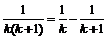 , получим
, получим
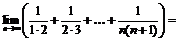
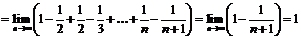 .
.
Пример 19. Найти 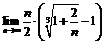 .
.
Используя тождество 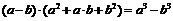 , будем иметь:
, будем иметь:
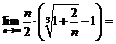
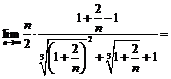
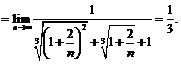
Теоремы о пределах, связанные с неравенствами
1) Принцип двухстороннего ограничения.
Если 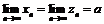 и для всех
и для всех 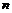 , начиная с некоторого
, начиная с некоторого 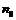 ,
, 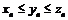 , то
, то 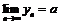
2) Теорема о предельном переходе в неравенстве.
Если 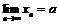 и для всех
и для всех 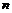 , начиная с некоторого
, начиная с некоторого 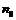 ,
, 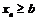 (или
(или 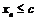 ), то
), то 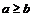 (или
(или 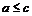 ).
).
Пример 20. Найти 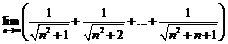 .
.
В рассматриваемой сумме содержится  слагаемое, наименьшее из которых
слагаемое, наименьшее из которых 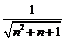 , а наибольшее
, а наибольшее 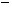
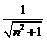 , поэтому
, поэтому 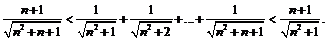
Так как
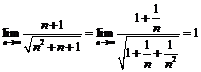 и
и 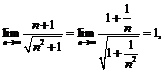 то
то 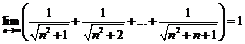 .
.
Пример 21. Доказать, что 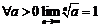 .
.
Пусть сначала  .
.
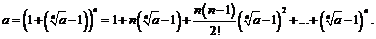 В сумме справа все слагаемые положительны, поэтому
В сумме справа все слагаемые положительны, поэтому 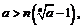 откуда
откуда 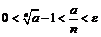 . Следовательно, при
. Следовательно, при 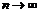
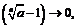 т.е.
т.е. 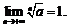
Если 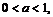 то
то 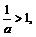 поэтому по доказанному выше
поэтому по доказанному выше 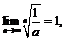 откуда следует, что
откуда следует, что 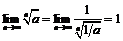 .
.
Пример 22. Доказать, что 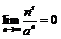 для
для 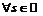 и
и 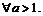
По условию 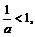 поэтому
поэтому 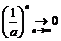 (доказано в примере 14). Если при этом
(доказано в примере 14). Если при этом 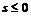 , то по лемме о бесконечно малых
, то по лемме о бесконечно малых 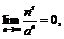 так как последовательность
так как последовательность 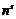 ограничена:
ограничена: 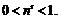
Пусть теперь 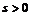 . Тогда найдется такое натуральное число
. Тогда найдется такое натуральное число 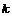 , что
, что 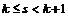 и будет выполняться неравенство
и будет выполняться неравенство 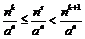 . Покажем, что крайние члены этого неравенства стремятся к общему пределу.
. Покажем, что крайние члены этого неравенства стремятся к общему пределу.
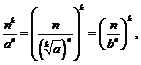 где
где 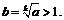
Но
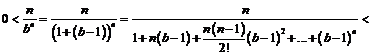
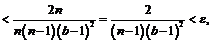 если
если 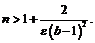
Таким образом, 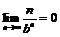 , а тогда, применяя теорему о пределе произведения, получим, что
, а тогда, применяя теорему о пределе произведения, получим, что 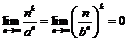 .
.
Аналогично 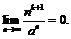 Принцип двустороннего ограничения приводит нас к выводу:
Принцип двустороннего ограничения приводит нас к выводу: 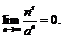
Пример 23. Доказать, что 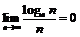 для
для 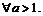
Требуется для 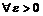 указать
указать 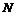 такое, что для
такое, что для 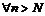 имеет место неравенство:
имеет место неравенство: 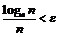 . Преобразуем данное неравенство:
. Преобразуем данное неравенство:
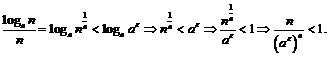
При  и
и 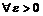
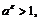 поэтому по результатам предыдущего примера
поэтому по результатам предыдущего примера 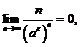 что означает, что для
что означает, что для 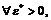 в том числе и для
в том числе и для 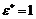 , найдётся
, найдётся 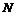 такое, что для всех
такое, что для всех 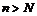 выполняется:
выполняется: 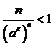 , что равносильно
, что равносильно 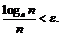
Пример 24. Доказать: 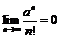 для
для 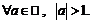
Каково бы ни было вещественное число 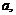 можно указать такое натуральное число
можно указать такое натуральное число 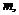 что
что 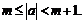 Тогда
Тогда
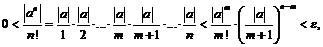
откуда получим: 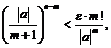 затем логарифмируя, будем иметь:
затем логарифмируя, будем иметь:
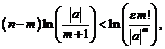
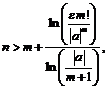 ведь
ведь 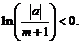
Следовательно, 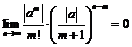 , и по теореме о двустороннем ограничении получаем требуемое.
, и по теореме о двустороннем ограничении получаем требуемое.