Если последовательность монотонна, начиная с некоторого номера, и ограничена, то эта последовательность имеет конечный предел.
Пример 25. Доказать, что последовательность сходится, если 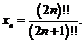
Применим теорему о пределе монотонной последовательности. Для доказательства монотонности рассмотрим отношение: 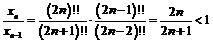 для
для 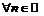 , т.е.
, т.е. 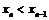 - данная последовательность монотонно убывает. При этом
- данная последовательность монотонно убывает. При этом 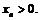 Следовательно, существует
Следовательно, существует 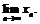
Пример 26. Доказать, что последовательность 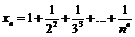 имеет предел.
имеет предел.
Последовательность  монотонно возрастает, ибо
монотонно возрастает, ибо 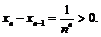 Покажем, что
Покажем, что  ограничена сверху.
ограничена сверху.
Так как 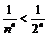 для
для 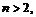 то
то 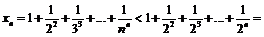
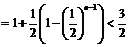 , и последовательность сходится.
, и последовательность сходится.
Пример 27. Доказать, что последовательность
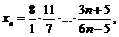
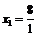 сходится и найти ее предел.
сходится и найти ее предел.
Рассмотрим
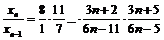
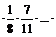
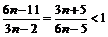 , если
, если 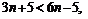
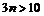
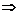
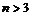 .
.
При этом 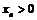 - по теореме о пределе монотонной последовательности сходимость доказана. Обозначим
- по теореме о пределе монотонной последовательности сходимость доказана. Обозначим 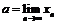 . Тогда, переходя к пределу при
. Тогда, переходя к пределу при 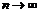 в равенстве
в равенстве 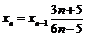 , получим:
, получим: 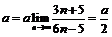 , откуда следует, что
, откуда следует, что 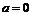 .
.
Пример 28. Доказать, что последовательность
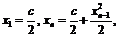
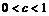 сходится и найти её предел.
сходится и найти её предел.
Вычислим 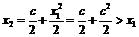 . Рассмотрим разность
. Рассмотрим разность
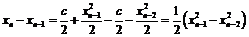 .
.
Используем метод математической индукции:
имеем 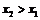 , предположим, что
, предположим, что 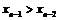 , тогда из предыдущего равенства получим:
, тогда из предыдущего равенства получим: 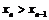 - последовательность монотонно возрастает. По условию
- последовательность монотонно возрастает. По условию 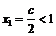 . Если предположить, что
. Если предположить, что 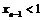 , то из равенства
, то из равенства 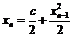 следует, что
следует, что 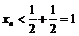 -последовательность ограничена сверху. По теореме о пределе монотонной последовательности существует
-последовательность ограничена сверху. По теореме о пределе монотонной последовательности существует 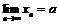 , поэтому для определения
, поэтому для определения 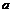 перейдем к пределу при
перейдем к пределу при 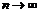 в равенстве
в равенстве 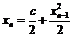 , будем иметь:
, будем иметь: 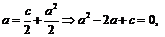
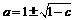 . Из двух возможных значений
. Из двух возможных значений 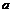 выбираем то, которое со знаком ²-², ибо предел заведомо не может быть больше 1 (ведь
выбираем то, которое со знаком ²-², ибо предел заведомо не может быть больше 1 (ведь 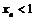 , следовательно, и
, следовательно, и 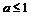 по теореме о предельном переходе в неравенстве).
по теореме о предельном переходе в неравенстве).
Итак, 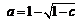 .
. 
Пример 29.Доказать, что последовательность имеет предел и найти его, если: 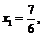
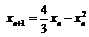 .
. 
Вычислим несколько первых членов данной последовательности:
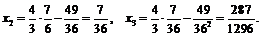
Рассмотрим разность:
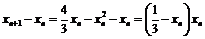 , откуда следует, что если
, откуда следует, что если 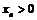 и
и 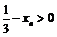 , т.е.
, т.е. 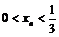 , то последовательность возрастающая, а если
, то последовательность возрастающая, а если 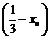 и
и  разных знаков, т.е.
разных знаков, т.е. 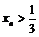 , то последовательность убывающая. Поскольку
, то последовательность убывающая. Поскольку 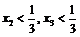 , будем доказывать, что
, будем доказывать, что 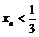 , методом математической индукции. Из предположения
, методом математической индукции. Из предположения 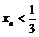 получим:
получим:
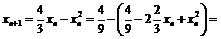
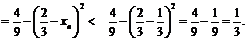



Итак доказано одновременно и монотонное возрастание последовательности, и ее ограниченность сверху. Следовательно, существует 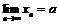 . Переходя к пределу в равенстве
. Переходя к пределу в равенстве 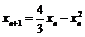 , будем иметь:
, будем иметь: 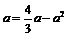 ,
, 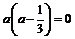
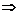
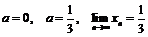 .
.
Пример 30. Доказать, что последовательность
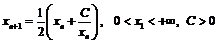
сходится и найти ее предел.
Рассмотрим рекуррентную формулу:
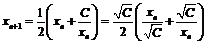
Обозначим 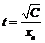 , тогда в скобках получим
, тогда в скобках получим 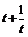 . Но так как
. Но так как 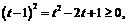
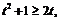 то для
то для 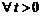 ,
, 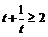 , следовательно,
, следовательно, 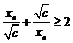 (ведь для
(ведь для 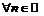
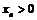 ).
).
Тогда 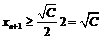 - последовательность ограничена снизу. При этом
- последовательность ограничена снизу. При этом 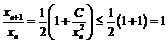 - последовательность монотонно убывающая.
- последовательность монотонно убывающая.
Следовательно, существует 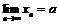 и, перейдя к пределу при
и, перейдя к пределу при 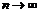 в рекуррентной формуле, получим:
в рекуррентной формуле, получим: 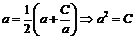 ,
, 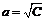 .
.
Фундаментальные последовательности. Критерий Коши
Определение.
Последовательность  называется фундаментальной, если для
называется фундаментальной, если для 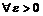 существует такое натуральное число N, что для всех
существует такое натуральное число N, что для всех 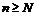 и всех
и всех 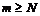 верно неравенство:
верно неравенство: 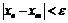 .
.
Данное определение можно сформулировать по-другому:
для 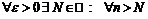
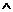
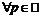 имеет место неравенство:
имеет место неравенство: 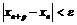 .
.
Критерий Коши.
Для того, чтобы последовательность  имела конечный предел, необходимо и достаточно, чтобы она была
имела конечный предел, необходимо и достаточно, чтобы она была
фундаментальной.
Пример 31. Доказать, что последовательность 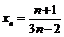 фундаментальна.
фундаментальна.
Рассмотрим модуль разности:
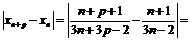
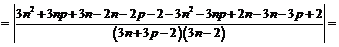
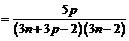 .
.
Для 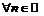 и
и 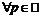 справедливо неравенство:
справедливо неравенство: 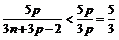 , так как
, так как  . Поэтому
. Поэтому
для 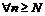 и
и 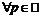 имеет место
имеет место 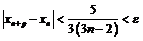 , откуда следует:
, откуда следует: 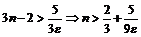 .
.
Пример 32. Доказать, что последовательность 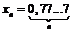 фундаментальна.
фундаментальна.
Так как 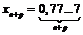 , то
, то
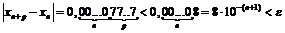 , откуда
, откуда
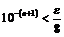 и, логарифмируя:
и, логарифмируя: 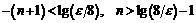 ,
, 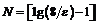 .
.
Пример 33. Доказать, что последовательность
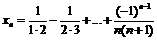 фундаментальна.
фундаментальна.
Так как
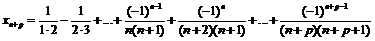 , то
, то
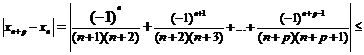
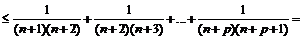
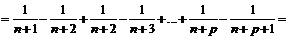
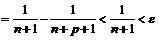
для 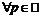 , откуда
, откуда 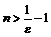 , т.е.
, т.е. 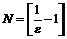 .
.
Пример 34. Доказать, что последовательность
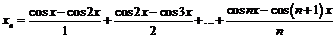
фундаментальна.
Учитывая, что
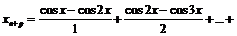
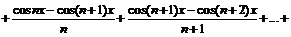
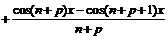 ,
,
получим:
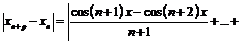
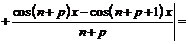

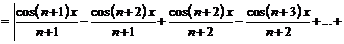
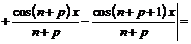
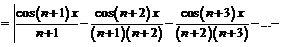
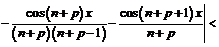
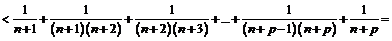
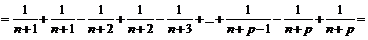
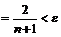 , откуда
, откуда 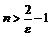 . При этом использовалось тождество
. При этом использовалось тождество
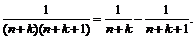
Таким образом, для 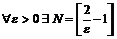 , что для
, что для 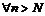 и
и 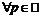 имеет место неравенство
имеет место неравенство 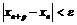 .
.
Пример 35. Доказать, пользуясь критерием Коши, что последовательность 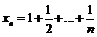 расходится.
расходится.
Запишем отрицание критерия Коши: последовательность расходится тогда и только тогда, когда 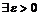
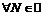
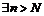
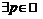 такие, что
такие, что 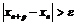 .
.
Учитывая, что 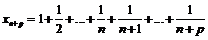 , будем иметь:
, будем иметь:
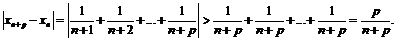 Если
Если 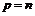 , то
, то 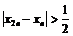 .
.
Итак, 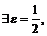 что какое бы
что какое бы 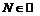 мы ни выбрали, взяв
мы ни выбрали, взяв 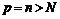 , получим:
, получим: 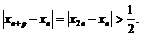
Пример 36. Доказать, что последовательность 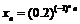 не является фундаментальной.
не является фундаментальной.
Eсли 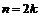 , то
, то 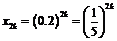 , если же
, если же 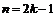 , то
, то 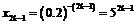 . Поэтому, если
. Поэтому, если 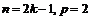 , то
, то
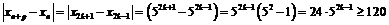 для
для 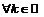 .
.
Итак, 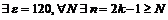 и
и 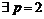 , что имеет место неравенство
, что имеет место неравенство 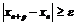 .
.
Пример 37. Доказать, что последовательность
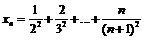 не является фундаментальной.
не является фундаментальной.
Так как
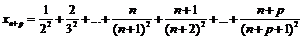 , то
, то
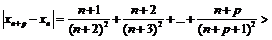
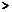
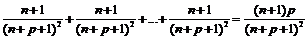
Пусть теперь 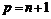 , тогда
, тогда 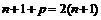 и
и 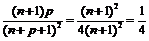 .
.
Таким образом, 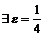 , что
, что 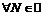
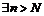 и
и 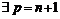 такие, что
такие, что 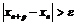 .
.
Пример 38. Доказать, что последовательность 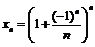 не является фундаментальной.
не является фундаментальной.
Рассмотрим
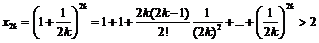
(все слагаемые положительны) и
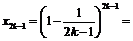
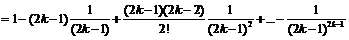
- выражение содержит 2k слагаемых, k из которых положительны, а k - отрицательны, знаки слагаемых чередуются. При этом отношение модулей соседних слагаемых равно 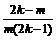 , для
, для 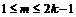 , т.е. меньше 1 для
, т.е. меньше 1 для 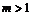 .
.
Поэтому, группируя слагаемые по два, получим, во-первых:
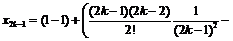
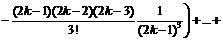
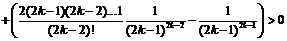 ,
,
во-вторых,
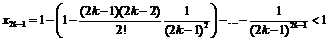 .
.
Тогда 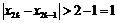 .
.
Таким образом, 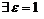
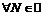
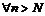 и
и 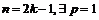 , что
, что 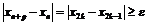 .
.
Упражнения для самостоятельной работы 1. Пусть 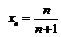
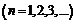 . Доказать, что
. Доказать, что 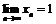 , определив для каждого e > 0 число
, определив для каждого e > 0 число 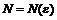 такое, что
такое, что 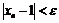 , если
, если 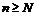 .
.
Заполнить следующую таблицу:
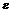
| 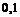
| 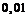
| 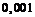
| 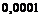
|
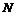
|
2. Доказать, что 
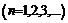 есть бесконечно малая, т.е. имеет предел, равный
есть бесконечно малая, т.е. имеет предел, равный 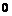 , указав для всякого
, указав для всякого 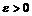 число
число 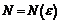 такое, что
такое, что 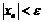 при
при 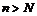 , если
, если
а) 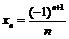 ; в)
; в) 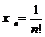 ;
;
б) 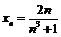 ; г)
; г) 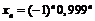 .
.
Для каждого из этих случаев заполнить таблицу:
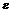
| 0,1 | 0,01 | 0,001 | 0,0001 |
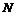
|
3. Доказать, что последовательности
а) 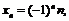 б)
б) 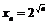 , в)
, в) 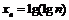 ,
, 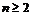 имеют бесконечный предел при
имеют бесконечный предел при 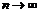 (т.е. являются бесконечно большими), определив для всякого E > 0 число
(т.е. являются бесконечно большими), определив для всякого E > 0 число 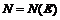 такое, что
такое, что 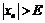 при
при 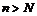 .
.
Для каждого из этих случаев заполнить таблицу:
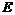
| 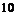
| 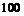
| 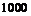
| 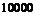
|
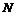
|
4. Сформулировать с помощью неравенств следующие утверждения:
а) 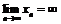 ; б)
; б) 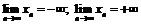 .
.
5. Найти 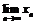 , если:
, если:
1) 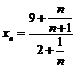 ; 2)
; 2) 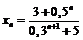 ; 3)
; 3) 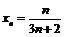 ; 4)
; 4) 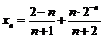 ; 5)
; 5) 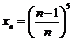 ; 6)
; 6) 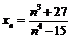 ; 7)
; 7) 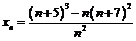 ; 8)
; 8) 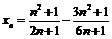 ; 9)
; 9) 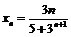 ; 10)
; 10) 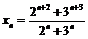 ; 11)
; 11) 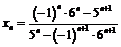 .
.
Найти:
6. 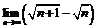 ; 7.
; 7. 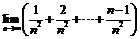 ;
;
8. 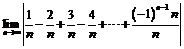 ; 9.
; 9. 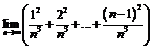 ; 10.
; 10. 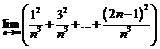 ;
;
11. 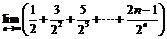 ; 12.
; 12. 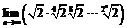 .
.
Докажите следующие равенства:
13. 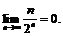 14.
14. 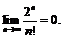 15.
15. 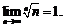
Пользуясь теоремой о существовании предела монотонной и ограниченной последовательности, доказать сходимость следующих последовательностей:
16. 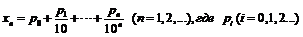 - целые неотрицательные числа, не превышающие 9, начиная с
- целые неотрицательные числа, не превышающие 9, начиная с 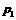 .
.
17. 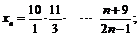
18. 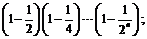
19. 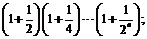
20. 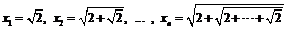 ;
;
21. 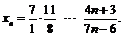
22. Доказать, что последовательность  имеет предел и найти его, если:
имеет предел и найти его, если:
1) 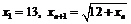 ;
;
2) 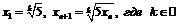 ;
;
3) 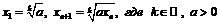 ;
;
4) 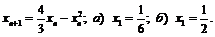
Пользуясь критерием Коши, показать сходимость следующих последовательностей:
23. 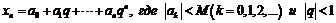 ;
;
24. 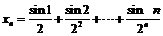 ;
;
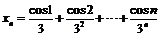 ;
;
25. 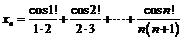 ;
;
26. 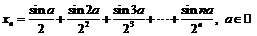 ;
;
27. 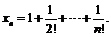
Пользуясь отрицанием критерия Коши, доказать, что следующие последовательности расходятся:
28. 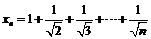 ; 29.
; 29. 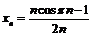 ;
;
30. 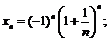 31.
31. 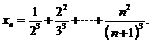
Мощность множества
Аналогом понятия «количество элементов конечного множества» в случае бесконечного множества является понятие «мощность» множества.
Определение
Говорят, что два множества 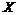 и
и 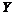 имеют одинаковое число элементов или одинаковую мощность, если между их элементами может быть установлено взаимно однозначное соответствие.
имеют одинаковое число элементов или одинаковую мощность, если между их элементами может быть установлено взаимно однозначное соответствие.
Из данного определения следует, что множество натуральных чисел 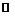 содержит столько же элементов, сколько и множества чётных или нечётных чисел. Действительно, каждому натуральному числу
содержит столько же элементов, сколько и множества чётных или нечётных чисел. Действительно, каждому натуральному числу 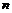 сопоставим чётное число
сопоставим чётное число 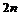 или нечётное число
или нечётное число 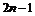 .
.
Таким образом, для бесконечных множеств известный принцип Аристотеля «часть меньше целого» уже не является справедливым. В смысле сделанного определения часть может быть равна целому!
Возможность для множества быть равномощным своей части является характерным признаком бесконечных множеств. По Дедекинду множество называется конечным, если оно не равномощно никакому своему собственному подмножеству; в противном случае множество называется бесконечным.
 Пример 1. Показать, что на гипотенузе прямоугольного треугольника точек «столько же», сколько и на катете.
Пример 1. Показать, что на гипотенузе прямоугольного треугольника точек «столько же», сколько и на катете.
Доказательство очевидно из рисунка. Достаточно спроектировать точки гипотенузы на соответствующий катет. Однако стоит помнить, что мощность множества и длина – это различные понятия, из совпадения мощностей множеств не вытекает равенство длин катета и гипотенузы.
Пример 2. Доказать равномощность интервала действительных чисел 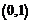 и множества действительных чисел
и множества действительных чисел 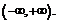
В данном случае проще непосредственно указать закон, задающий взаимнооднозначное отображение. Например, 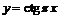 .
.
Определение
Множество, равномощное множеству натуральных чисел, называется счётным.
Согласно данному определению множество счётно, если оно содержит бесконечно много элементов, и притом все они могут быть расположены в виде последовательности, занумерованной натуральными числами.
Справедливы следующие леммы:
- Любое бесконечное множество содержит счётное подмножество.
- Любое бесконечное подмножество счётного множества счётно.
Из последнего утверждения следует, что мощность счётного множества – наименьшая бесконечная мощность.