Равномерное распределение.

Дискретные распределения.

.

Биномиальное распределение. (Распределение Бернулли) Предположим, что производятся независимые испытания и при каждом испытании может быть два исхода — успех с вероятностью р или неудача с вероятностью q (р + q = 1). Например, стрельба по цели (при каждом выстреле два исхода — попадание или непопадание); проверка наугад вы­бранного изделия, которое может оказаться качественным или бракованным; подбрасывание симметричной монеты (при каждом подбрасывании появится герб или решка). Термины «успех» и «неудача» употребляются для удобства, важно только, чтобы при каждом испытании было два исхода.

Предположим, что произведено п испытаний, пусть x — число успехов при п испытаниях.

 

Данная случайная величина принимает значения от 0 до n.

P(ξ=m)=P_n(m)=C_n^mp^mq^n-m.

Согласно биному Ньютона:

(p+q)ⁿ= C_n⁰pⁿq⁰+ C_n¹p^n-1q¹+…=

= = =

 

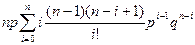Если k=i-1

 

= =np

 

Найдем наибольшее значение для биноминального распределения.

 

 

k>np-q – число меньше единицы

P(ξ=k+1)<P(ξ=k)

k>np-q – число больше единицы

P(ξ=k+1)>P(ξ=k)

K=np-q –тут может быть дробным числом. тогда в [k] максимум.

Если k целое число. То у нас два максимума.

 

Другой способ вычисления P_x и M_x.

 

 

_{= ; ;}

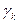
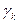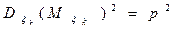
Геометрическое распределение.

Приводиться ряд экспериментов. Где может быть успех или неуспех.

 

ξ—кол-во Неуспехов до первого успеха

P(ξ=m)=q^mp

Данная формула имеет свойство отсутвия посследствия P(ξ=m+n/ ξ>=n)= P(ξ=m)

 

P(ξ=m+n/ ξ>=n)= P(ξ=m)=

 

 

 

 

 

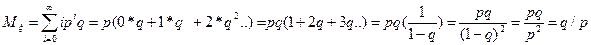
Распределение Пуассона.

Пусть события одно за другим с интенсивностью λ к моменту времени t₁ t₂.Причем интенсивность не зависит от τ(его величины и местоположения)—простейший однородный стационарный поток относительно λ.

Случайная величина ξ кол-во событий за время τ.

Для подсчета разделим процесс τ на n- частей так,чтобы промежутки 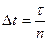, и за это время могло произойти или не произойти событие.Вероятность поступления одного события за время равно тогда

P(ξ=m)=

 

 

 

При следующие пределы равны:

 

 

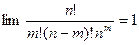
P(ξ=m)=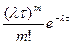

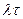=a – среднее кол-во событий за время τ.

 

P(ξ=m)=

А – параметр распределения Пуассона

=1;

;

 

 

 

Математическое ожидание равно дисперсии.

 

Гипергеометрическое распределение.

 

Имеется N объектов. Среди них m обладают свойством «1», а N-m обладают свойством «2». для исследования взято l объектов.

ξ – кол-во объектов обладающих свойством «1» среди l, взятых на исследование

 

P(ξ=k) =

Непрерывные распределения.

 

Равномерное распределение.

 

Равномерное распределение определяет случайную величину заданную на отрезке [a;b].

 

 

 

 

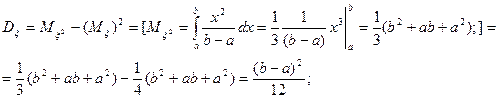
Показательное распределение.

 

Показательное распределение характеризует время безотказной работы в условиях эксперемента имеющего Распределение Пуассона.

ξ-время до первого отказа прибора:

F(x)=P(ξ<x)=1-p(0)=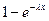

 

т.к. P(0)=

p(x)=F(x)=

 

 

;

 

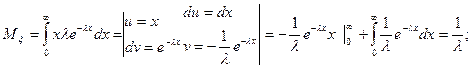
Распределение нормальное.

Интеграл Лапласса 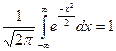, если выполним замену , то получим наше распределение:

 

 

p(x)= ;

 

 

 

 

Т.к. =0,

а =1.

 

 

σ—среднеквадратическое отклонение нормального распределения.

 

 

Распределение Коши.

 

Пусть имеется источник излучения α-частиц.

ξ- случайная величина пересечения частицы с осью координат x.

 

 

 

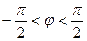
P(ξ<x)=P(tg (φ)< ).

P(φ<arctg )=

 

 

p(x)=P’(x)=

Распределение Коши не имеет мат.ожидания.

 

Распределение Вейбула –Гнеденко.

 

Это распределение используется в теории вероятностии и в теории надежности.

 

ק(x)=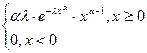

 

-- функция интенсивности потока событий.

Если α=1, то поучаем показательное распределение.

 

Распределение Лапласа.

 

p(x)=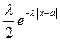

Данное распределение симметрично.