Множества
После проработки этой главы Вы должны уметь:
а) использовать систему записи множеств;
б) определять, равны ли данные два множества или является ли одно из данных множеств подмножеством другого;
в) находить объединение, пересечение и разность двух данных множеств.
Что такое множество?
В математике часто рассматриваются наборы объектов различных типов. Например, можно рассматривать:
· решения квадратного уравнения;
· точки на окружности;
· простые числа меньше 100;
· вершины треугольника;
· область определения вещественной функции.
Понятие множества предоставляет единую структуру, необходимую для систематического рассмотрения подобных наборов.
Множество можно рассматривать как набор объектов, таких как числа, точки, функции или даже другие множества. Каждый объект в множестве называется его элементом; элементы принадлежат множеству.
Ограничений на типы объектов, которые могут находиться в множестве, нет при условии, что множество задано таким образом, что мы, в принципе, можем определить, принадлежит ли данный элемент множеству.
Такое описание может быть произведено многими способами. Например, можно определить множество S как множество чисел из списка 4, 9, 3, 2. Это описание позволяет определить, что, к примеру, число 2 принадлежит S, а число 1 — нет. Такое множество может быть проиллюстрировано схемой, как на полях; она называется диаграммой Венна в честь жившего в XIX веке кембриджского математика Джона Венна.
Также множество E может быть задано утверждением: «пусть E будет множеством всех чётных целых чисел». Такое описание позволяет нам определить, является ли данный объект элементом E, узнав, является ли он чётным целым числом; например, 6 принадлежит E, а 5 — нет.
Некоторые множества используются так часто, что для их записи заняты специальные символы.
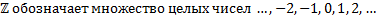
Мы используем символ ∈, чтобы показать принадлежность множеству; например, чтобы показать, что 7 — это элемент ℕ, мы пишем:
.
Чтобы показать, что 9 — это не элемент ℕ, мы пишем:
.
Также символ ∈ используется, чтобы ввести символ, обозначающий произвольный элемент множества. Например, пишут
чтобы показать, что x — это произвольный (неопределённый) элемент множества ℝ. Иногда говорят, что x — это вещественная переменная. Вообще переменная — это символ (типа x или n), который обозначает произвольный элемент множества.
Упражнение 1.1
Система записи множеств
Теперь изучим некоторые формальные способы записи множеств.
Множество с небольшим количеством элементов может быть задано перечисление этих элементов в фигурных скобках. Например, можно задать множество A, состоящее из первых пяти натуральных чисел, так:
Принадлежность множеству не зависит от порядка, в котором перечислены его элементы, поэтому множество A может быть с тем же успехом задано так:
Таким же образом можно задать множество B вершин квадрата, показанного на полях:
Можно даже задать множество C, элементами которого будут три множества {1, 3, 5}, {9, 4} и {2}:
Множество из одного элемента, как, например, {2}, называется одноэлементным, или одноточечным. (Не путайте множество {2} и число 2.)
Упражнение 1.2
Не имеет значения, указываем ли мы элемент множества в фигурных скобках несколько раз: мы по-прежнему описываем множество, состоящее из каждого из элементов по отдельности. Например, {1, 2, 3, 3} и {1, 2, 3} — это одно и то же множество. Тем не менее, записи одного элемента несколько раз обычно избегают.
В случае множеств с большим числом элементов перечислять все элементы непрактично, поэтому иногда для указания на продолжение определённой модели принадлежности элементов множеству используются три точки (называемые многоточием, или эллипсисом). Например, множество первых 100 натуральных чисел можно задать, написав {1, 2, 3,..., 100}.
Использование многоточия может быть расширено и на некоторые бесконечные множества. Например, множество всех натуральных чисел натуральных чисел может быть записано как {1, 2, 3,...}. Недостаток такой записи заключается в том, что модель, обозначенная многоточием, может быть двусмысленной. Например, непонятно, какое множество описывает запись {3, 5, 7,...}: множество всех нечётных простых чисел или множество всех нечётных чисел больше единицы. По этой причине такая запись может быть использована, только когда модель принадлежности очевидна или когда даются дополнительные пояснения.
Другой способ задания множества — это использование переменных для построения объектов необходимого типа и последующая запись условий, которым должны отвечать эти объекты. Например, рассмотрим интервал (3, ∞), которые состоит из всех такие действительных чисел x, что x > 3. Используя систему записи множеств, мы можем записать его как
что читается так: множество действительных x таких, что x больше 3.
Часто с помощью такой записи множество может быть описано несколькими разными способами. В частности, для обозначения произвольного элемента множества может быть использована другая буква:
Если после двоеточия нужно поставить больше одного условия, то они разделяются запятой или словом «и». Так, полуинтервал (0, 1] может быть записан так:
хотя обычно эти неравенства совмещают и пишут
Иногда удобно задать множество, написав перед двоеточием выражение от одной или нескольких переменных, а после — условия, накладываемые на переменные. Например, множество чётные целых чисел меньше 100 может быть задано так:
Так же, как и при записи множества как списка элементов, запись одного элемента несколько раз значения не имеет. Например, записи
задают одно и то же множество.
Запись множеств полезна, когда нам нужно указать множество решений одного или нескольких уравнений. Например, решения уравнения 
составляют множество
Множество решений уравнений зависит от множества значений, из которого выбираются решения. Например, множество решений уравнения
—
это
если нас интересуют действительные решения, но если мы рассматриваем только целые решения, то это будет
В этой части книги мы полагаем, что решения берутся из 
, если не оговорено иное.
Иногда у уравнения нет действительных решений, поэтому в множестве его решений нет элементов. Такое множество называется пустым множеством и обозначается символом ⌀. Например,
Пример 1.1
Решение
Упражнение 1.3
1.3 
Множества на плоскости
В части I1 Вы познакомились с плоскостью 
и увидели, что любая точка на плоскости может быть представлена как упорядоченная пара 
по отношению к данной паре осей. Множество точек из называется множеством на плоскости, или плоской фигурой. Простые примеры множеств на плоскости — это прямые и окружности.
Прямые
Рассмотрим прямую линию l c наклоном a и пересечением с осью ординат на расстоянии b от начала координат. Эта прямая — это набор всех таких точек плоскости , что 
. Используя систему записи множеств, запишем это так:
.
(Иногда в качестве краткой записи этого множества используется фраза «прямая ».)
Прямую, параллельную к оси Oy и отстоящую от неё на расстояние c, записывают так:
.
Упражнение 1.4
Окружности
Единичная окружность U — это множество точек плоскости , расстояние от которых до точки начала координат 
равно 1. По теореме Пифагора, это точки , удовлетворяющие уравнению 
, так что единичная окружность записывается так:
.
В общем случае окружность C c радиусом r и центром в точке 
— это множество точек , лежащих от точки на расстоянии r. По теореме Пифагора, это точки , удовлетворяющие уравнению 
, так что единичная окружность записывается так:
.
Упражнение 1.5
Полуплоскости, круги и другие множества на плокости
Рассмотрим прямую
.
Эта прямая делит на три разные части: саму линию l, множество H 1 точек, лежащих над прямой, и множество H 2 точек, лежащих под прямой.
Рассмотрим произвольную точку 
из H 1, как показано на полях. Точка 
лежит на прямой l под P, как показано на рисунке, так что y > 1 – x. Аналогично, для любой точки 
из H 2 выполняется y < 1 – x. Таким образом,
и 
.
(На графиках, когда показанное множество на плоскости не включает граничную линию, мы рисуем её пунктиром.)
Множество точек с одной стороны от прямой, возможно, также вместе с точками самой прямой, называется полуплоскостью. Полуплоскость, не включающая точки прямой, задаётся аналогично вышеприведённым примерам H 1 и H 2. Соответствующие полуплоскости, включающие точки прямой получаются заменой строгих неравенств на нестрогие.
Теперь рассмотрим единичную окружность
.
Эта окружность делит плоскость на три разные части: саму окружность U, множество D 1 точек, лежащих внутри окружности, и множество D 2 точек, лежащих вне окружности.
Условие того, что точка (x, y) лежит внутри U — это то, что расстояние от неё до начала координат меньше единицы, то есть и квадрат этого расстояния тоже меньше единицы. Таким образом,
.
Аналогично,
.
Множество точек внутри окружности, возможно, вместе с точками самой окружности, называется кругом. Если нам нужно включить в круг точки самой окружности, мы заменяем в определении множества D 1 строгое неравенство на нестрогое.
Теперь рассмотрим множество точек, лежащих внутри квадрата с вершинами (0, 0), (1, 0), (1, 1) и (0, 1). Это множество можно записать как
.
Если в это множество надо включить стороны квадрата, мы меняем строгие неравенства на нестрогие. На рисунке такое множество мы бы показали, заменив пунктиры сплошными линиями.
Упражнение 1.6
Этот подраздел мы завершаем рассмотрением графика вещественной функции. В части I1 мы нарисовали график вещественной функции f, нанося на плоскость точки вида (x, f (x)) для каждого элемента x из области определения функции A. Из этого вытекает следующее формальное определение графика.
Определение График вещественной функции 
— это множество 
.
Упражнение 1.7