ДО 3 БАЛЛОВ ЗА КОНСПЕКТ
ЛЕКЦИЯ 1.2.
Основные операции над множествами
Операции над множествами
Определение 1. Объединением(суммой)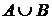 
двух множеств А и В называется множество, состоящее из тех и только тех элементов, которые принадлежат хотя бы одному из этих двух множеств.
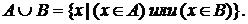
Еще будем писать так: 
.
В устной или письменной речи операцию объединения описывают союзом или.
Непосредственно из определения операции объединения следует справедливость и такого утверждения: если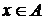 
, то элемент 
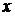принадлежит объединению множества 
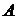со всяким другим множеством 
. Будем писать: 
.
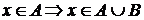Что же означает условие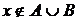 
? Из определения операции объединения следует, что если 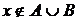, этот элемент не может входить ни в одно из данных двух множеств, то есть 
Пример. Пусть 
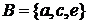. Тогда 
Пусть 
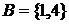. Тогда 
Определение.Пересечением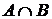 
(или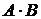 
, или АВ) двух множеств А и В называется множество, состоящее из тех и только тех элементов, которые принадлежат обоим множествам.
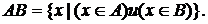
По-другому: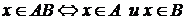 
.
Но если 
, он не принадлежит и пересечению 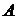с любым другим множеством. Будем писать: 
.
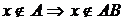В устной или письменной речи операции пересечения соответствует союз и.
Таким образом, чтобы элемент 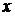не принадлежал пересечению 
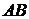, необходимо и достаточно, чтобы он не принадлежал хотя бы одному из двух множеств, т.е.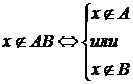 
Пример.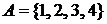 
, 
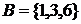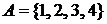. Тогда 
, 
. Тогда 
Определение. Два множества называются непересекающимися, если АВ=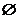 
.
Определение. Пусть e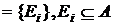 
- семейство множеств Ei, каждое из которых включено во множество А. Семейство e называется покрытием множества А, если всякий элемент множества А входит хотя бы в одно множество семейства e. Таким образом,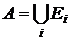 
Пример.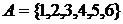 
. Тогда семейства
e 1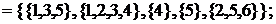 
e 2 
e 3 
- этопокрытия множества А.
Определение. Покрытие e называется разбиением множества А, если всякий элемент множества А принадлежит ровно одному множеству семейства e. Таким образом, 
и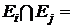 
Æ, если i¹j.
Пример 5.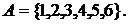 
Тогда семейства
e 1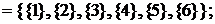 
e 2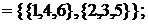 
e 3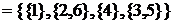 
образуют разбиения множества А.
Определение.Разностью 
множеств А и В называется множество, состоящее из тех и только тех элементов, которые принадлежат множеству А и не принадлежат множеству В.
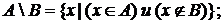
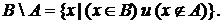
Иная запись: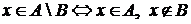 
.
Из этого определения следует, что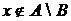 
тогда и только тогда, когда или 
. Итак, 
.
Пример. 
, 
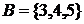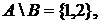
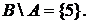
. Т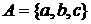огда 
, 
. Тогда 
Æ,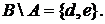 
Итак, если 
, то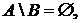 
так как во множестве А нет ни одного элемента, который не ходил бы в множество В. Обратно, если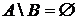 
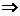
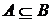, так как каждый элемент множества А принадлежит и В.
Определение.Симметрической разностью А 
В (или А Å В)множеств А и В называется множество, состоящее из тех и только тех элементов, которые принадлежат ровноодному из данных множеств
Или так: 
.
Но тогда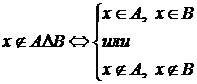 
.
Пример.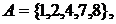 
Тогда 
, 
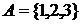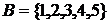. Тогда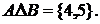 
Таким образом,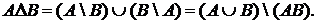 
Определение.Дополнением 
множества А доуниверсума U называют множество, состоящее из тех и только тех элементов, которые не принадлежат А.
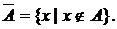
Иная запись: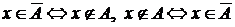 
.
В устной речи операции дополнения соответствует частица не.
Пример.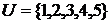 
, 
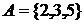. Тогда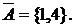 
Таким образом,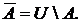 
Утверждение.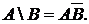 
Доказательство. Докажем, что множества 
и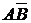 
состоят из одних и тех же элементов. Используя понятие подмножества, можно сказать, что А = В Û А Í В и В Í А (множества А и В состоят из одних и тех же элементов).
а. Пусть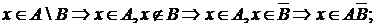 
б. Пусть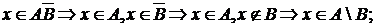 
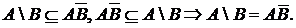
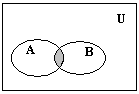
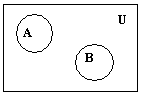
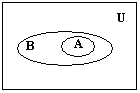
Диаграммы Венна
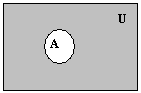
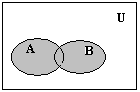
На диаграммах Венна универсум изображается прямоугольником или квадратом, а множества – областями внутри универсума. Точки – это элементы универсума. Проиллюстрируем диаграммами Венна введенные определения (рис.1).
 |
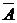
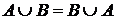
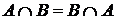
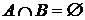
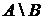
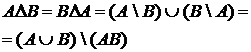
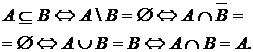
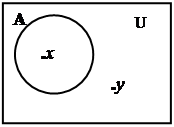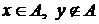
Рис. 1.