Пусть  Каковы бы ни были заданные подмножества
Каковы бы ни были заданные подмножества  универсума U, справедливы соотношения
универсума U, справедливы соотношения
1. Идемпотентность.

2. Коммутативность.

3. Ассоциативность.
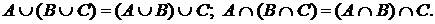
Дистрибутивность.

2. Законы поглощения.

3. Свойства нуля.

4. Свойства единицы.

5. Инволютивность.

6. Законы де Моргана.

10. Свойства дополнения.

Доказательство этих равенств большей частью совершенно элементарно. Построим доказательства одного из законов дистрибутивности и одного из законов де Моргана.
Утверждение.  .
.
Доказательство.

 .
.

Пусть 
 Þ
Þ

 .
.
 .
.
Утверждение.  .
.
Доказательство.





 ,
,  .
.
Законы коммутативности и ассоциативности легко распространяются на случай объединения (пересечения) любого конечного числа множеств. Именно, в какой бы последовательности не объединялись (пересекались) данные множества  , в результате получится одно и тоже множество, которое обозначается
, в результате получится одно и тоже множество, которое обозначается  . Объединение состоит из тех и только тех элементов, которые входят хотя бы в одно из данных множеств (пересечение содержит те и только те элементы, которые входят во все множества одновременно).
. Объединение состоит из тех и только тех элементов, которые входят хотя бы в одно из данных множеств (пересечение содержит те и только те элементы, которые входят во все множества одновременно).
Запишем обобщение законов дистрибутивности и де Моргана

Доказательство проводится, например, методом математической индукции.
Примеры решения задач
Пример 2. Доказать что  Û
Û  Û
Û  Û
Û  .
.
Решение. Для доказательства 12 указанных утверждений достаточно доказать любую замкнутую цепочку из четырех утверждений вида



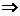

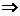

Доказательство.
а)  Þ
Þ 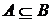 .
.

б) 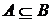 Þ
Þ  .
.

 по определению объединения множеств;
по определению объединения множеств;
А È В = В.
в)  Þ
Þ  .
.
 по определению пересечения множеств;
по определению пересечения множеств;

АВ = А.
г)  Þ
Þ  .
.
 противоречие
противоречие
д)  Þ
Þ 

Пример 3. Верны ли следующие рассуждения? Проиллюстрировать обоснование истинности (ложности) этих рассуждений диаграммами Венна.
а) Если А, В, С – такие подмножества универсума U, что АВ  и А È С Í В, то АС = Æ.
и А È С Í В, то АС = Æ.
Пояснение. Условия АВ  и А È С Í В называются посылками или допущениями. Вывод АС = Æ называется заключением или следствием из данных посылок. Совокупность посылок и заключения называется рассуждением. Если можно привести хотя бы один пример (в частности, построить диаграмму Венна), в котором посылки истинны, а заключение ложно, то рассуждение считается неверным.
и А È С Í В называются посылками или допущениями. Вывод АС = Æ называется заключением или следствием из данных посылок. Совокупность посылок и заключения называется рассуждением. Если можно привести хотя бы один пример (в частности, построить диаграмму Венна), в котором посылки истинны, а заключение ложно, то рассуждение считается неверным.
Решение. В данном случае опровергнуть рассуждение невозможно, строгое доказательство справедливости рассуждения написано под диаграммой (рис. 2)

 Æ.
Æ.
Рис.2
б) Если А, В, С – такие подмножества универсума U, что  и
и  то В = Æ.
то В = Æ.
Решение. Диаграмма Венна приведена на рис.3. Рассуждение ложно.
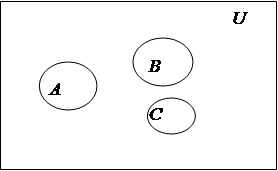


Рис.3
Пример 4. Из 100 студентов английский язык знают 28 человек, немецкий – 30, французский – 42, английский и немецкий – 8, английский и французский – 10, немецкий и французский – 5, все языки знают 3 человека. Сколько человек не знают ни одного языка? Сколько человек знают в точности два языка? Сколько человек знают английский или французский языки, но не знают немецкий?
Решение. Построим диаграмму Венна (рис. 4.). Универсум U – это множество всех студентов, A 1- множество студентов, знающих английский язык; A 2- множество студентов, знающих немецкий язык; A 3- множество студентов, знающих французский язык. Области  в общем случае разбивают прямоугольник универсума на 8 областей. Внутри каждой области записано число элементов, лежащих в этой области (мощность соответствующего множества). Известно, что
в общем случае разбивают прямоугольник универсума на 8 областей. Внутри каждой области записано число элементов, лежащих в этой области (мощность соответствующего множества). Известно, что
 Нужно найти
Нужно найти  ,
,  ,
,  .
.

Рис. 4
 ;
;  ;
;  .
.
Литература: [2], [3], [4], [9], [10], [18], [19], [20], [23]