ТЕМА: «ВПИСАННАЯ И ОПИСАННАЯ ОКРУЖНОСТИ»
Вписанная окружность
Окружность вписана в многоугольник, если она касается всех его сторон.
В любой треугольник можно вписать окружность и притом только одну.
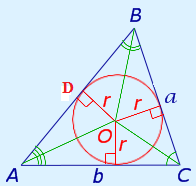
Центр вписанной в треугольник окружности лежит в точке пересечения биссектрис треугольника.
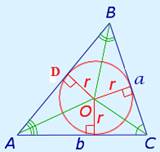
OD =r –радиус окружности. ОD 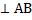 . Чтобы построить радиус вписанной окружности нужно из ее центра опустить перпендикуляр к стороне треугольника. Полученный отрезок будет являться радиусом описанной окружности. . Чтобы построить радиус вписанной окружности нужно из ее центра опустить перпендикуляр к стороне треугольника. Полученный отрезок будет являться радиусом описанной окружности.
| 
|
| Если окружность вписана в четырёхугольник, то суммы противоположных сторон этого четырёхугольника равны: AB + CD = BC + AD. | 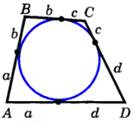
|
| Описанная окружность Окружность описана около многоугольника, если все вершины многоугольника лежат на окружности. Около любого треугольника можно описать окружность. Центр описанной около треугольника лежит в точке пересечения серединных перпендикуляров к сторонам треугольника. OD, OE,OF- серединные перпендикуляры. ОА=ОВ=ОС =R –радиус описанной окружности. Чтобы построить радиус описанной окружности необходимо точку пересечения серединных перпендикуляров соединить с вершиной треугольника. | 
|
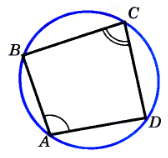
Если окружность описана около четырёхугольника, то суммы его противоположных углов равны:
ÐA + ÐC = ÐB + ÐD.
и ÐA + ÐC 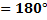
| 
|
Площадь треугольника равна произведению его полупериметра на радиус вписанной в него окружности.
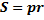
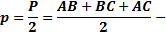
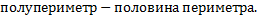 Если около четырехугольника можно описать окружность (т.е сумма противолежащих углов равна
Если около четырехугольника можно описать окружность (т.е сумма противолежащих углов равна 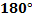 )то его площадь можно посчитать по формуле )то его площадь можно посчитать по формуле 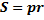 где
где 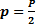 – полупериметр. – полупериметр.
| 
|
Прежде чем приступить к решению задач необходимо прочитать §4 стр-178-182 учебника.
Разберем задачи по теме.
|
|
Задача 1.
Найдите радиус окружности, описанной около прямоугольного треугольника АВС, если его катеты равны 24 и 10 см

| Дано: DАВС – прямоуг. АВ – гипотенуза; АС = 24 см; ВС = 10 см; Окр. (О; r) – опис-я. Найти: r -? |
1) Точка. С лежит на окружности (треугольник вписанный). Если ÐС – прямой, тогда дуга АВ = 180  , значит АВ является диаметром окружности. Þ О Î АВ, радиус описанной около прямоугольного треугольника окружности равен половине гипотенузы; так как АВ –диаметр, а ОВ=ОА=
, значит АВ является диаметром окружности. Þ О Î АВ, радиус описанной около прямоугольного треугольника окружности равен половине гипотенузы; так как АВ –диаметр, а ОВ=ОА=  АВ
АВ
2) DАВС – прямоугольный, ÐС – прямой, по теореме Пифагора:
АВ2 = АС2 + ВС2 = 576 + 100 = 676;
АВ = 26 (см);
3) r =  AB = 13 (см).
AB = 13 (см).
Ответ: r = 13 см.
Задача 2. По данным рисунка найдите радиус вписанной в равнобедренный треугольник окружности.
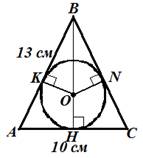
| Дано: DАВС – р/б; АС – основ-е; ВН – высота; Окр. (О; r) – впис.; АВ = 13 см; АС = 10 см Найти: r -? |
1) DАВС – р/б, АС – основание, ВН – высота Þ ВН – биссектриса (по свойству высоты р/б треугольника, проведённой к основанию) Þ О Î ВН (центр вписанной в треугольник окружности лежит в точке пересечения биссектрис);
2) Пусть ОН ^ АС, ОК, ON – радиусы вписанной окружности Þ ON ^ ВС, OK ^ АВ (радиусы, проведённые в точку касания, по свойству касательной), ОН = ON = OK;
3) DАВС – р/б, АС – основание, ВН – высота Þ ВН – медиана (по свойству высоты р/б треугольника, проведённой к основанию) Þ АН = НС = 5 см;
4) DАВН – прямоугольный, по теореме Пифагора: АВ2 = ВН2 + АН2;
169 = ВН2 + 25;
ВН = 12 (см).
5) AK = AH = 5 см (свойство отрезков касательных) Þ ВК = 13 – 5 = 8 (см);
6) DОВК – прямоугольный (OK ^ АВ), ОК = OH Þ BO = BH – OH = 12–ОК;
По теореме Пифагора:
|
|
ВО2 = ОК2 + ВК2;
(12 – ОК)2 = ОК2 + 64;
144 – 24ОК + ОК2 = ОК2 + 64;
80 = 24ОК
ОК =  (см).
(см).
Ответ: радиус вписанной окружности r=  см.
см.
Задача 3 Найдите площадь равнобедренного треугольника с основанием АВ = 6, если расстояние от центра описанной окружности до АВ равно 4.
Напоминаю, расстояние от точки до прямой – длина перпендикуляра, опущенного к данной прямой.
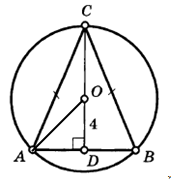
| Дано: DАВС – р/б; АВ – основ-е; CD – высота; Окр. (О; r) – опис-я.; АВ = 6; OD = 4. Найти: SABC -? |
1) OD – расстояние от центра описаннной окружности до АВ. Значит OD – серединный перпендикуляр (проходит через середину АВ и перпендекулярен АВ). СD – высота, проведённая к основанию равнобедренного DАВС Þ СD – серединный перпендикуляр к АВ Þ О Î CD так как центр описанной около треугольника окружности лежит в точке пересечения серединных перпендикуляров к сторонам треугольника.
2) О – центр описанной около равнобедренного DАВС окружности Þ АО = СО = ВО – радиусы описанной окружности;
3) DAOD – прямоугольный (CD – высота), AD = 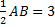 . По теореме Пифагора:
. По теореме Пифагора:
АО2 = AD2 + DO2 = 9 + 16 = 25;
AO = 5;
4) СD = OD + CO = 4 + 5 = 9;
5) 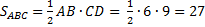 .
.
Ответ: 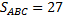 .
.
Задача 4.