
| Дано: ABCD – р/б трап.; BC, AD – основания; Окр. (О; r) – впис.; ВС = 4 см; АВ = 10 см. Найти: r -? |
1) ABCD – р/б трап-я, ВС, AD – основания; Окр.(О; r) – впис-я Þ ОР = ОН = ОМ = ON = r, ОР ^ ВС, ОН ^ АD, ON^AB, OM^CD (по свойству касательной), РН – высота трапеции;
2) Окр.(О, r) – вписанная Þ АВ + СD = BC + AD (свойство четырёхугольника, в который вписана окружность);
20 = 4 + AD; AD = 16.
3) Проведем ВК, СЕ – высоты трапеции. DАВК = DCDE (прямоугольные, по гипотенузе (АВ = CD) и острому углу (ÐА = ÐD)) Þ AK = ED.
ВСЕК – прямоугольник Þ ВС = ЕК = 4 (см);
АК = ED = (AD – EK): 2 = (16 – 4): 2 = 6 (см).
По теореме Пифагора (DАВК):
АВ2 = АК2 + ВК2;
100 = 36 + ВК2;
ВК2 = 64;
ВК = 8 (см).
4) ВК = РН = 8 см, ОР = ОН = 4 см.
Ответ: радиус вписанной окружности – 4 см.
Проверка базовых теоретических знаний учащихся
Пройти тест.
Девочки проходят 1 вариант.
Мальчики 2 вариант.
Тест по теме «Вписанная и описанная окружности».
Вариант I.
1. Каждая точка биссектрисы неразвернутого угла равноудалена от его
а) углов; б) сторон; в) вершин.
2. Каждая точка серединного перпендикуляра к отрезку
а) равноудалена от концов этого отрезка;
б) равноудалена от середины этого отрезка;
в) равноудалена от углов.
3. Если все стороны многоугольника касаются окружности, то окружность называется
а) описанной около многоугольника;
б) вписанной в треугольник;
в) вписанной в многоугольник.
4. В любой треугольник можно вписать только
а) две окружности;
б) три окружности
в) одну окружность.
5. В любом вписанном четырехугольнике сумма противолежащих углов равна
а) 3600; б) 1800; в) 900.
6. Центр вписанной окружности лежит в точке пересечения
а) медиан;
б) серединных перпендикуляров;
в) биссектрис.
7. Описанная около треугольника окружность изображена на рисунке:
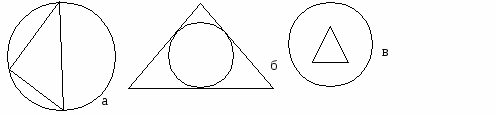
8. Вписанная в четырехугольник окружность изображена на рисунке:

Тест по теме «Вписанная и описанная окружности».
Вариант II.
1. Каждая точка, равноудаленная от сторон угла, лежит на его
а) медиане; б) высоте; в) биссектрисе.
2. Серединным перпендикуляром к отрезку называется прямая,
а) проходящая через середину данного отрезка и перпендикулярная к нему;
б) проходящая через середину данного отрезка;
в) перпендикулярная к отрезку.
3. Если все вершины многоугольника лежат на окружности, то окружность называется
а) описанной около многоугольника;
б) описанной около треугольника;
в) вписанной в многоугольник.
4. Около любого треугольника можно описать только
а) две окружности;
б) одну окружность;
в) три окружности.
5. В любом описанном четырехугольнике суммы противолежащих сторон
а) равны; б) равны радиусу; в) равны периметру.
6. Центр описанной окружности лежит в точке пересечения
а) медиан;
б) серединных перпендикуляров;
в) биссектрис.
7. Вписанная в треугольник окружность изображена на рисунке:
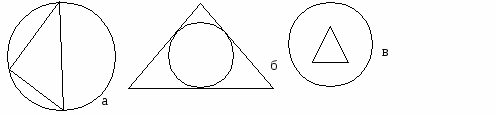
8. Описанная около четырехугольника окружность изображена на рисунке:

САМОСТОЯТЕЛЬНАЯ РАБОТА.
Задача 1.

Задача 2.

Задача 3

ВНИМАНИЕ! КЛЮЧ К ТЕСТУ И САМОСТОЯТЕЛЬНУЮ РАБОТУ ПРИСЫЛАТЬ ЛИЧНЫМ СООБЩЕНИЕМ В ВК 23.04.20 ДО 20.00.
Д/З§4 и конспект изучить. Все определения и теоремы знать наизусть. По конспекту обязательно выучить где расположен радиус вписанной и описанной окружности.
Реш. задачи 693,697, 706.