Лекция 7.2 Непараметрические методы сравнения нескольких групп данных
К настоящему времени Вы заработали баллов: 0 из 0 возможных.
КРИТЕРИЙ H КРУСКАЛ - УОЛЛИСА ДЛЯ СРАВНЕНИЯ ТРЕХ И БОЛЕЕ НЕЗАВИСИМЫХ СОВОКУПНОСТЕЙ ДАННЫХ
Критерий H Крускал Уоллиса (Краскал –Уоллиса) является непараметрическим аналогом ANOVA для независимых совокупностей. Основные условия и ограничения заключаются в следующем:
· Выборочные данные могут иметь любой закон распределения (не требует проверки на нормальность распределения);
· применим как для метрических, так и для порядковых переменных
Статистические гипотезы:
· Нулевая гипотеза Н0: выборочные совокупности однородны;
· Альтернативная гипотеза Н1: не все совокупности данных неоднородны.
Для расчета эмпирического значения H Крускала Уоллиса используется следующая формула:

| rij - ранг i испытуемого в j группе n – количество данных (испытуемых) в одной группе наблюдений N – общее количество наблюдений (все испытуемые во всех группах вместе взятых) |
Если объем каждой выборки больше 5, то показатель H имеет хи квадрат распределение Пирсона со степенями свободы df=c-1 (критические значения находят по таблице χ2 Пирсона), где с – количество сравниваемых групп. В противном случае необходимо пользоваться специальными таблицами критических значений Н Крускала Уоллиса. (Наследов. А.Д., 2007; стр.372)
Схема проверки нулевой гипотезы
Этап 1 Объединить значения всех групп и проранжировать их (rij)
Этап 2 Для каждой группы в отдельности рассчитать сумму рангов (Σ rij)
Этап 3 Рассчитать эмпирическое значение статистики Н-Крускала-Уоллиса по формуле.
Этап 4 Если каждая выборка больше 5 человек, то по таблицам критических значений χ2 - распределение Пирсона со степенями свободы df = c–1 (с – количество групп) найти значения для уровней значимости 0,05 и 0,01.
Этап 5 Сравнить эмпирическое значение показателя H с критическими значениями хи-квадрат. Если эмпирическое значение H превышает критическое χ2, тогда нулевая гипотеза отвергается на соответствующем уровне значимости
ПРИМЕР 1
Исследователь изучал особенности временной перспективы у людей с химическими зависимостями. Он набрал три группы испытуемых: (0) контрольная группа, лица, (1) страдающие алкоголизмом, (2) наркотической зависимостью. Исследователь предположил, что люди с химическими зависимостями в большей степени ориентированы на получение удовольствия настоящего (гедонистическое настоящее) в сравнении с обычными людьми.
Всем испытуемым был предложен опроник ZTPI Ф.Зимбардо. Анализируемая переменная – временная ориентация на гедонистическое настоящее. Объем каждой группы составил 15 человек (мужчины)
Показатели по шкале «гедонистическое настоящее» опросника ZTPI:
Контрольная группа (К): 2,2 3,1 2,9 3,1 3 3,9 3,1 3,2 3,1 2,7 2,6 2,7 3,1 3,7 3,3
Группа с алкогольной зависимостью (А): 2,7 3 4,1 3,8 3,1 2,3 3,3 3,7 3,2 3,7 3,9 3,5 2,9 2,9 4,1
Группа с наркотической зависимостью (Н): 3,4 3,7 2,9 3,3 4,4 3,9 3,7 4,3 3,3 4 3,3 3,7 3,1 4,1 3
Статистические гипотезы:
· Нулевая гипотеза: выраженность гедонистического настоящего не связана с наличием химических зависимостей.
· Альтернативная гипотеза: выраженность гедонистического настоящего связана с наличием химических зависимостей.
Пример 1 / этап 1 и 2
Объединить значения всех групп и проранжировать их (rij). При этом мы должны сохранить информацию о принадлежности значения к той или иной группе.
1. Контрольная группа (К): 2,2 3,1 2,9 3,1 3 3,9 3,1 3,2 3,1 2,7 2,6 2,7 3,1 3,7 3,3
2. Группа с алкогольной зависимостью (А): 2,7 3 4,1 3,8 3,1 2,3 3,3 3,7 3,2 3,7 3,9 3,5 2,9 2,9 4,1
3. Группа с наркотической зависимостью (Н): 3,4 3,7 2,9 3,3 4,4 3,9 3,7 4,3 3,3 4 3,3 3,7 3,1 4,1 3

Этап 2
Для каждой группы в отдельности рассчитать сумму рангов (Σ rij). Для этого рассортируем ранги по группам и найдем сумму.
1. Контрольная группа (К): 1+3+5+5+8,5+12+17+17+17+17+17+21,5+25+32,5+38= 236,5
2. Группа с алкогольной зависимостью (А): 2+5+8,5+8,5+12+17+21,5+25+29+32,5+32,5+36+38+42+42= 351,5
3. Группа с наркотической зависимостью (Н): 8,5+12+17+25+25+25+28+32,5+32,5+32,5+38+40+42+44+45= 447
Пример 1 / этап 3
1. Контрольная группа (К): 236,5
2. Группа с алкогольной зависимостью (А): 351,5
3. Группа с наркотической зависимостью (Н): 447
Этап 3 Рассчитать эмпирическое значение статистики Н-Крускала-Уоллиса по формуле.
| rij - ранг i испытуемого в j группе n – количество данных (испытуемых) в одной группе наблюдений N – общее количество наблюдений (все испытуемые во всех группах вместе взятых) |
Числитель в формуле = сумму рангов каждой группы возвести в квадрат (1 шаг) и разделить на объем группы (2 шаг), получившиеся значения сложить (3 шаг) и умножить на 12 (4 шаг).
| К контр | А алко | Н нарк | |
Сумма рангов

| 236,5 | 351,5 | |
(шаг 1) Квадрат суммы рангов

| 55932,25 | 123552,3 | |
(шаг 2) квадраты разделить на объем группы (15 человек)

| 55932,25/15 = 3728,817 | 123552,3/15 = 8236,817 | 199809/15 = 13320,6 |
(шаг 3) сумма значений из шага 2

| 3728,817 + 8236,817 + 13320,6 = 25286,23 | ||
(шаг 4) умножить на 12

| 25286,23 * 12= 303434,8 | ||
Разделить на N(N+1)

| 303434,8 / 45 / 46 = 146,59 | ||
| Отнять 3*(N+1) | 146,59 – 3*46 = 8,59 |
Таким образом, эмпирическое значение Н = 8,59
пример 1 / заключительные этапы
По таблицам χ2 - Пирсона находим критические значения для степеней свободы df = c–1=3-1 =2и уровней значимости 0,05 и 0,01.
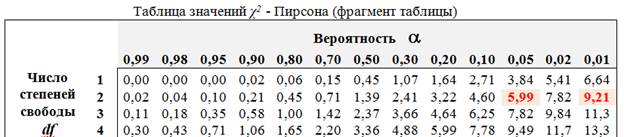
Таким образом, χ2 0,05 = 5,99 и χ2 0,01 = 9,21.
Этап 5 Сравнить эмпирическое значение с критическими. Нулевая гипотеза отвергается, если эмпирическое значение больше критических.
Эмпирическое χ2 = 8,59
критическое χ 2 0,05 = 5,99
критическое χ 2 0,01 = 9,21
Какой вывод следует сформулировать в данном примере?
Поскольку эмпирическое значение χ2 попадает в область критических отклонений, то отвергаем нулевую гипотезу на уровне значимости 0,05 и принимаем альтернативную о том, что выраженность гедонистического настоящего связана с наличием химических зависимостей.