
ВЫВОД: Поскольку эмпирическое значение χ2 попадает в область критических отклонений, то отвергаем нулевую гипотезу на уровне значимости 0,05 и принимаем альтернативную о том, что выраженность гедонистического настоящего связана с наличием химических зависимостей.
В контрольной группе показатель гедонистического настоящего ниже по сравнению с группой людей с наркотической зависимостью

КРИТЕРИЙ ФРИДМАНА ДЛЯ СРАВНЕНИЯ ТРЕХ И БОЛЕЕ ЗАВИСИМЫХ СОВОКУПНОСТЕЙ ДАННЫХ
Критерий Фридмана является непараметрическим аналогом ANOVA для зависимых совокупностей.Преимущество этого критерия заключается в том, что он прост в вычислении, не зависит от закона распределения случайной величины и его можно применять как для метрических, так и для порядковых переменных.
Статистические гипотезы:
1. Нулевая гипотеза Н0: выборочные совокупности однородны;
2. Альтернативная гипотеза Н1: не все совокупности данных неоднородны.
Для расчета эмпирического значения хи-квадрат Фридмана используется следующая формула:

| rij - ранг i испытуемого в j группе n – количество данных (испытуемых) в одной группе наблюдений с – количество групп наблюдений |
Если объем выборки больше 9, то показатель Фридмана имеет хи квадрат распределение Пирсона со степенями свободы df=c-1 (критические значения находят по таблице χ2 Пирсона). В противном случае необходимо использовать специальные таблицы критических значений χ2 Фридмана (Наследов. А.Д., 2007; стр.375).
Схема проверки нулевой гипотезы
Этап 1 Для каждого испытуемого проранжировать значения по условиям фактора (rij)
Этап 2Для каждого j-условия фактора рассчитать сумму рангов 
| |
| Этап 3Каждую сумму рангов возвести в квадрат | 
|
| Этап 4Квадраты сложить и умножить на 12 | 
|
| Этап 5Получившееся значение разделить на количество наблюдений во всех группах вместе взятых и на количество групп плюс 1. Далее вычесть 3 умноженное на количество наблюдений в одной группе и количество групп плюс 1. Это и есть эмпирическое значение хи квадрат Фридмана. | 
|
Этап 6 Если выборка больше 9 человек, то по таблицам критических значений χ2 - распределение Пирсона со степенями свободы df = c–1 (с – количество групп) находят значения для уровней значимости 0,05 и 0,01.
Этап 7 Сравнить эмпирическое значение показателя Фридмана с критическими значениями хи-квадрат. Если эмпирическое значение χr2 превышает критическое χ2, тогда нулевая гипотеза отвергается на соответствующем уровне значимости
Пример 2
Сохраняется ли ритм моторной активности в течении 30 секунд в теппинг тесте?
В этом тесте испытуемому предлагается лист бумаги, разделенный на 6 секторов. Ему необходимо как можно в более быстром темпе ставить точки в каждом секторе в течение 5 секунд.
Переменная: продуктивность (количество точек в каждом секторе)

Статистические гипотезы:
1. Нулевая гипотеза: продуктивность моторной активности стабильна в течение 30 секунд
2. Альтернативная гипотеза: продуктивность моторной активности различна на разных временных промежутках в течение 30 секунд.
Пример 2 / 1 и 2 этап
Для каждого испытуемого проранжировать значения по условиям фактора (rij)

Этап 2 Для каждого j-условия фактора рассчитать сумму рангов (Σrij)
Считаем сумму рангов для каждого сектора.
| Номер сектора | ||||||
| Испытуемый 1 | 1,5 | 3,5 | 3,5 | 1,5 | ||
| Испытуемый 2 | ||||||
| Испытуемый 3 | ||||||
| Испытуемый 4 | ||||||
| Испытуемый 5 | 2,5 | 2,5 | ||||
| Испытуемый 6 | 2,5 | 2,5 | ||||
| Испытуемый 7 | 3,5 | 3,5 | 1,5 | 1,5 | ||
| Испытуемый 8 | ||||||
| Испытуемый 9 | 2,5 | 2,5 | ||||
| Испытуемый 10 | 3,5 | 3,5 | ||||
| Сумма рангов Σrij | 49,5 | 27,5 |
Пример 2 / 3... 5 этапы
Этап 3 Каждую сумму рангов возвести в квадрат

Этап 4 Квадраты сложить и умножить на 12

(2450,25 + 1849 + 1681 + 841 + 756,25 + 400) * 12 = 7977,5 * 12 = 95730
Этап 5
| Получившееся значение разделить на количество наблюдений во всех группах вместе взятых n*c (10*6) и на количество групп плюс 1 (6 + 1). Далее вычесть 3 умноженное на количество наблюдений в одной группе (10) и количество групп плюс 1 (6 + 1). Это и есть эмпирическое значение хи квадрат Фридмана | 
|
χ2 = 95730 / (10*6*7) - 3*10*7= 17,93
Этап 6
По таблицам χ2 - распределение Пирсона находим критические значения для степеней свободы df = c–1= 6 – 1 = 5 и уровней значимости 0,05 и 0,01.
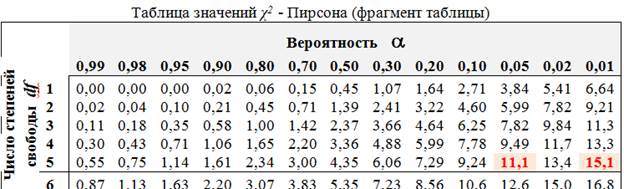
Таким образом, χ2 0,05 = 11,1 и χ2 0,01 = 15,1.
Этап 7 Сравнить эмпирическое значение с критическими. Нулевая гипотеза отвергается, если эмпирическое значение больше критических.
Эмпирическое χ2 = 17,9
χ2 0,05 = 11,1
χ2 0,01 = 15,1