ТЕМА: Работа и мощность цепи постоянного тока.
Работа, совершаемая электрическим полем при перемещении положительного заряда q вдоль неразветвленного участка а-Ь электрической цепи, не содержащего источников электрической энергии, равна произведению этого заряда на напряжение
между концами участка: А = qU. При равномерном движении заряда в течение времени t, т. е. при постоянном токе lаь = l, перемещаемый вдоль участка заряд равен
q= lt,
а совершаемая при этом работа равна
А= Ult.
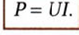Мощность равна скорости, с которой совершается работа
Основная единица измерения работы в СИ - gжоуль (Дж), мощности - ватт (Вт).Практической единицей измерения электрической энергии служит киловатт-час (кВт · ч), т. е. работа, совершаемая при неизменной мощности 1 кВт в течение 1 ч.
Так как 1 Вт · с = 1 Дж, то 1 кВт · ч = 3 600 ООО Дж = 3,6 МДж.
,ДЛЯ резистивных элементов выражение (2.30) можно преобразовать, воспользовавшись законом Ома:
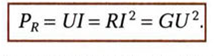
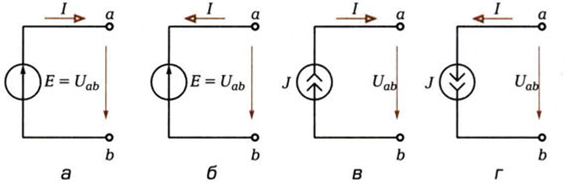
ДЛЯ источника ЭДС, положительное направление которой совпадает с выбранным положительным направлением тока (рис. 2.29, а), мощность сторонних сил.
Если направления ЭДС и тока противоположны, то мощность Рн = (рис. 2.29, 6). Аналогично мощность источника тока,
если направления тока в источнике J = I и напряжения между его выводами Иаь противоположны (рис. 2.29, в). В противном случае мощность Р1 = -И0ьl = -И0ь J (рис. 2.29, r).
Идеальные источники ЭДС и тока могут развивать бесконечно большую мощность. Подключим к каждому источнику приемник с сопротивлением нагрузки Rн. В первом случае, если Rн ~О, то ток I ~ 00 и мощность Рн = EI ~ оо, во втором случае, если Rн ~ оо,
то напряжение И ~ оо и мощность Р1 = UJ ~ оо. Мощность источника ЭДС и источника тока может иметь положительное и отрицательное значения, что соответствует передаче
энергии источником во внешнюю относительно него цепь и
получению им энергии и з этой цепи. В любой электрической цепи должен соблюдаться энергетический баланс - баланс мощностей: алгебраическая сумма мощностей всех источников энергии (в частности, источников тока и источников ЭДС) равна арифметической сумме мощностей всех приемников энергии (в частности, резистивных элементов):
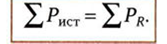
ТЕМА: Нелинейные электрические цепи постоянного тока. Нелинейные элементы.
Нелинейный резистивный элемент (выпрямительные диоды, стабилитроны, варисторы и т.д.) включается в цепь через два вывода. Его свойства определяет вольт амперная характеристика I(U) (рис. 2.30). Каждая точка БАХ определяет статическое
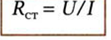
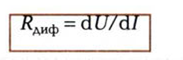
и дифференциальное:
Нелинейные свойства резистивных элементов лежат в основе принципа действия выпрямителей, стабилизаторов напряжения, усилителей и т. п. Расчет цепей с нелинейными резистивными элементами осуществляется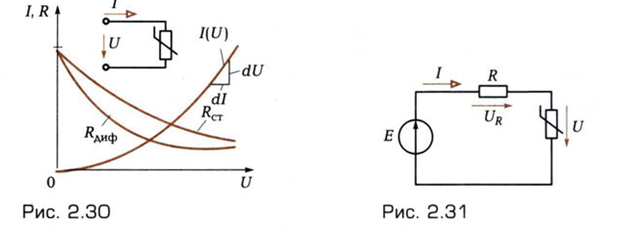 
графическими методами.
Рассмотрим расчет схемы с последовательным соединением источника ЭДС, линейного R и нелинейного резистивных элементов (рис. 2.31). На линейном резистивном элементе напряжение по второму закону Кирхгофа равно:
а ток по закону Ома с учетом (2.33) равен
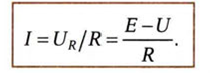
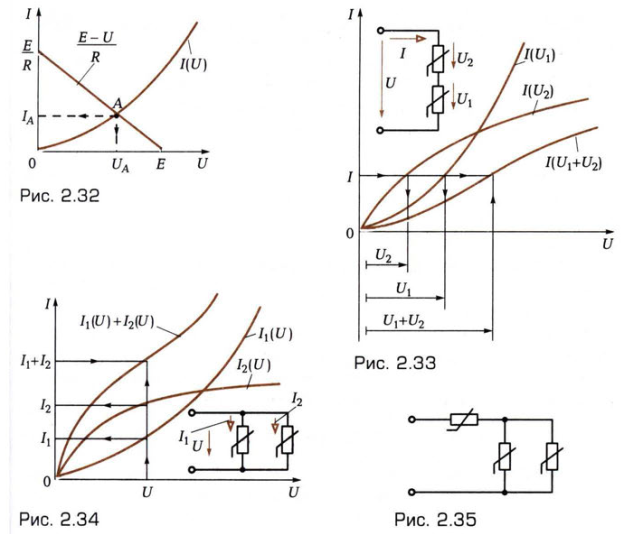
Уравнению (2.34) соответствует прямая линия, называемая нагрузочной характеристикой, проходящей через точки И = О, I = Е/ R на оси ординат и I = О, И = Е на оси абсцисс. Точка А пересечения нагрузочной характеристики и ВАХ!(И) нелинейного резистивного элемента определяет рабочий режим цепи (рис. 2.32): ток Iл и напряжение Ил- Графический метод расчета нелинейной цепи с помощью нагрузочной характеристики называется
методом нагрузочной характеристики.
Метод нагрузочной характеристики пригоден и в случаях, если цепь содержит последовательное или параллельное соединение нелинейных резистивных элементов с известными БАХ. Для этого необходимо в первом случае сложить БАХ нелинейных резистивных элементов по напряжению (рис. 2.33), а во втором - по току (рис. 2.34). Определив рабочую точку на результирующей БАХ методом нагрузочной характеристики, далее найдем ток и напряжение каждого нелинейного резистивного элемента. Аналогично рассчитывается цепь, которая содержит смешанное соединение нелинейных резистивных элементов (рис. 2.35). 