Для решения экономических задач с кредитованием вводятся условные обозначения:
1. S – сумма долга
2. r – начисляемые на эту сумму проценты
3. n – число лет или месяцев
4. Х – общая сумма выплат
Для удобства решения заполняется таблица, столбцы которой называются: долг, проценты, выплата. Число строк в таблице соответствует числу лет или месяцев, на которое взят кредит.
1) Долг на начало срока – это вся сумма, которую взяли в кредит. Таким образом, если кредит взят на n лет, то это означает, что сумму долга S разделили на n равных частей и что каждый год после выплаты сумма долга уменьшается на 1/n*S по сравнению с предыдущим долгом. Опираясь на это, заполняем первый столбик Долг.
2) Второй столбик % содержит произведение долга на данный период (первый столбик) и начисляемых на эту сумму процентов r/100.
3) Третий столбик – Выплата. Она состоит из суммы двух частей. Первая часть всегда фиксирована – это та часть, на которую долг уменьшается (1/n*S). Вторая часть – это проценты, которые рассчитаны во втором столбике.
| Долг | % | Выплата | |
| S | r/100 * S | 1/n * S + r/100 * S | |
| (n-1)/n * S | r/100 * (n-1)/n * S | 1/n * S + r/100 * (n-1)/n * S | |
| ... | |||
| n | 1/n * S | r/100 * 1/n * S | 1/n * S + r/100 * 1/n * S |
Таблица 1
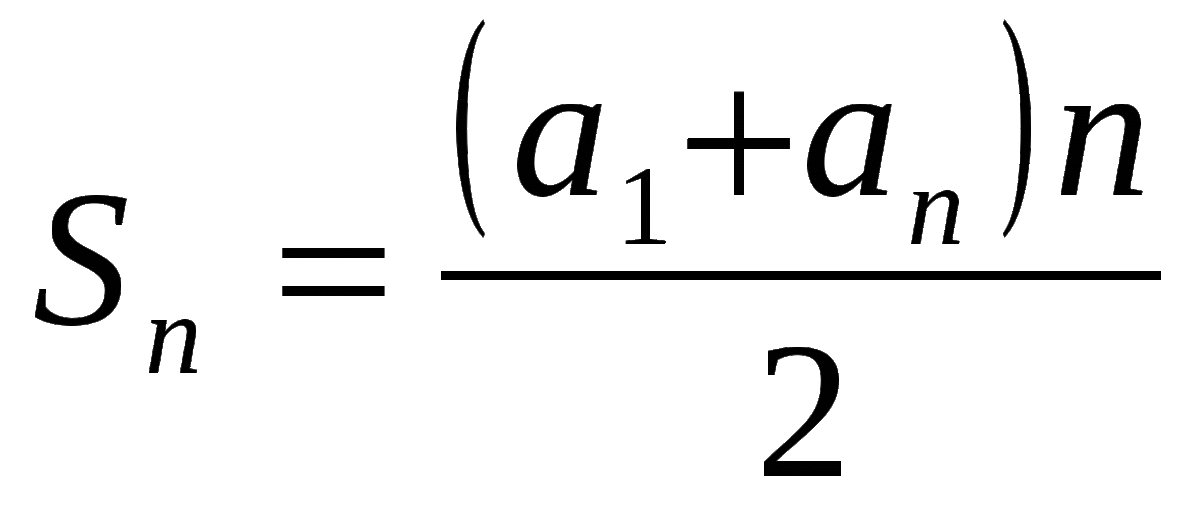
Для нахождения общей суммы выплат Х нужно сложить все выплаты, рассчитанные в третьем столбце. Будет проще, если складывать правую и левую часть по группам. Здесь для удобства можно использовать формулу суммы арифметической прогрессии.
Рис. 4 – Формула суммы арифметической прогрессии
Решение
Дано: S = 200 000 рублей, n = 4 года, r = 20% (20/100=1/5)
Найти: Х
| Долг | % | Выплата | |
| S | 1/5 * S | 1/4 * S + 1/5 * S | |
| 3/4 * S | 1/5 * 3/4 * S | 1/4 * S + 1/5 * 3/4 * S | |
| 2/4 * S | 1/5 * 2/4 * S | 1/4 * S + 1/5 * 2/4 * S | |
| 1/4 * S | 1/5 * 1/4 * S | 1/4 * S + 1/5 * 1/4 * S |
Таблица 5
|
|
Х = 4 * 1/4 * S + 1/5 * S (1 + 3/4 + 2/4 + 1/4) S = (1 + 1/4)/2 * 4 = 2,5
Х = S + 1/5 * S * 2,5
X = S + 0,5 * S
X = 1,5 * S
X = 1,5 * 200 000 = 300 000 (руб)
Ответ
Общая сумма выплат при дифференцированной схеме равна 300 000 рублей.
Решение задачи
С аннуитетным платежом
В задачах этого типа помимо суммы долга S,начисляемых на нее процентов r, числа месяцев или лет n и общей суммы выплат X для удобства решения вводится еще одно обозначение:
p = 1 + r/100
Для решения задач заполняется таблица, названия столбцов которой похожи с названиями дифференцированной таблицы: долг, долг + проценты, выплата. Эта таблица всегда будет одинаковая.
1) При аннуитетной схеме погашения кредита выплаты равны. Поэтому проще заполнить сначала третий столбик Выплата.
2) Второй столбик Долг + % – произведение р и долга на данный период.
3) Первый столбик Долг – это разность второго и третьего столбцов за предыдущий период.
| Долг | Долг + % | Выплата | |
| S | p * S | x | |
| p * S – x | p * (p * S – x) | x | |
| p * (p * S – x) – x | p * (p * (p * S – x) – x) | x | |
| p * (p * (p * S – x) – x) – x | p * (p * (p * (p * S – x) – x) – x) | x |
Таблица 3
В условии задачи этого типа всегда есть ключевая фраза. Например, «кредит будет полностью погашен четырьмя равными платежами». Это означает, что разность второго и третьего столбцов на период четвертого года равна нулю.
p * (p * (p * (p * S – x) – x) – х) – x = 0
p4 * S – p3 * x – p2 * x – p * x – x = 0
p4 * S = p3 * x + p2 * x + p * x + x
p4 * S = х * (р3 + р2 + р +1)
х = р4 * S/ (p3 + p2 + p + 1)
Общая сумма выплат Х при аннуитетной схеме погашения кредита – это сумма равных выплат х.
Х = 4х
Решение
Дано: S = 200 000 рублей, n = 4 года, r = 20% (р = 1 + 20/100 = 1,2)
|
|
Найти: Х
| Долг | Долг + % | Выплата | |
| S | p * S | х | |
| p * S – x | p * (p * S – x) | х | |
| p * (p * S – x) – x | p * (p * (p * S – x) – x) | х | |
| p * (p * (p * S – x) – x) – x | p * (p * (p * (p * S – x) – x) – x) | х |
Таблица 6
p * (p * (p * (p * S – x) – x) – х) – x = 0
p4 * S – p3 * x – p2 * x – p * x – x = 0
p4 * S = p3 * x + p2 * x + p * x + x
p4 * S = х * (р3 + р2 + р +1)
х = р4 * S/ (p3 + p2 + p + 1)
х = 1,24 * 200 000/ (1,23 + 1,22 + 1,2 + 1) = 2,0736 * 200 000/ (1,728 + 1,44 +
+ 1,2 + 1) = 414 720/5,368 = 77 258 (руб)
Х = 4х
Х = 4 * 77 258 = 309 032 (руб)
Ответ
Общая сумма выплат при аннуитетной схеме равна 309 032 рубля.
Результаты
Полученные вычисления представим в виде таблицы:
| Дифференцированный платеж | Аннуитетный платеж | |
| Основной долг(S) | 200 000 | 200 000 |
| Общая сумма выплат(X) | 300 000 | 309 032 |
Таблица 7
Таким образом, при аннуитетном платеже переплата больше. Значит кредит с дифференцированной схемой выплат выгоднее, чем кредит с аннуитетной на 9 032 рубля.
Вывод:наша гипотеза подтвердилась.

Рис. 7 – Дифференцированный платеж выгоднее
Анализ результатов
Почему так произошло, ведь условия (сумма кредита, срок погашения и проценты) были одни и те же? Ответ на этот вопрос дать сразу трудно. Но его хорошо видно на графиках.
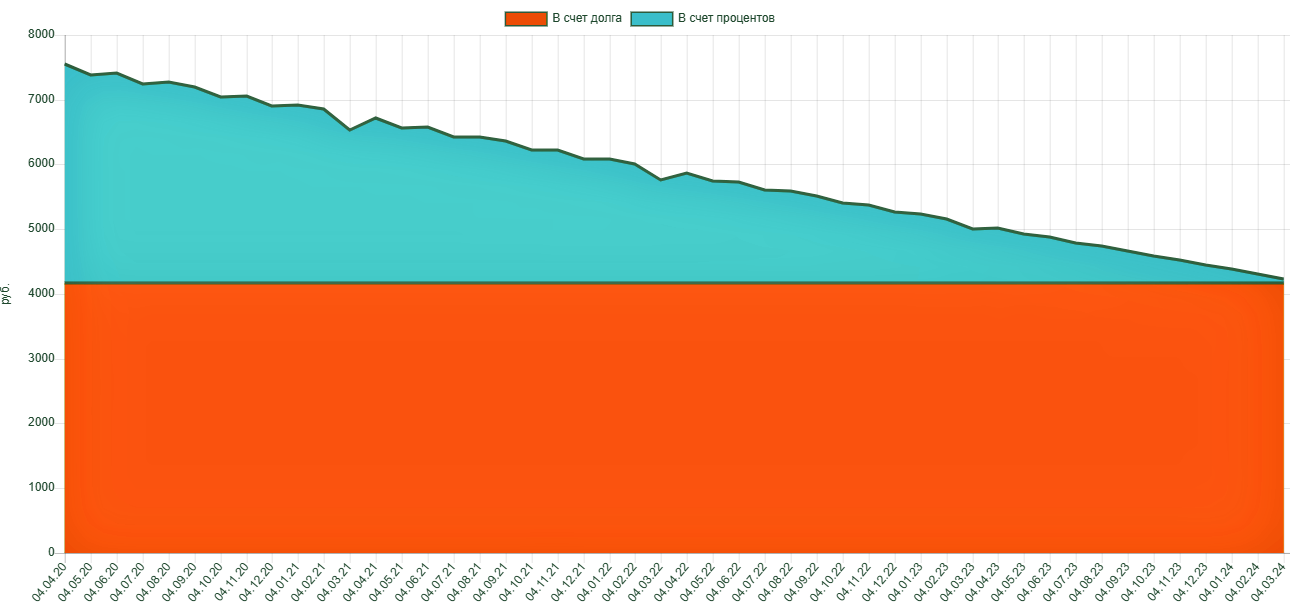
Рис. 8 – График дифференцированных выплат

Рис. 9 – График аннуитетных выплат
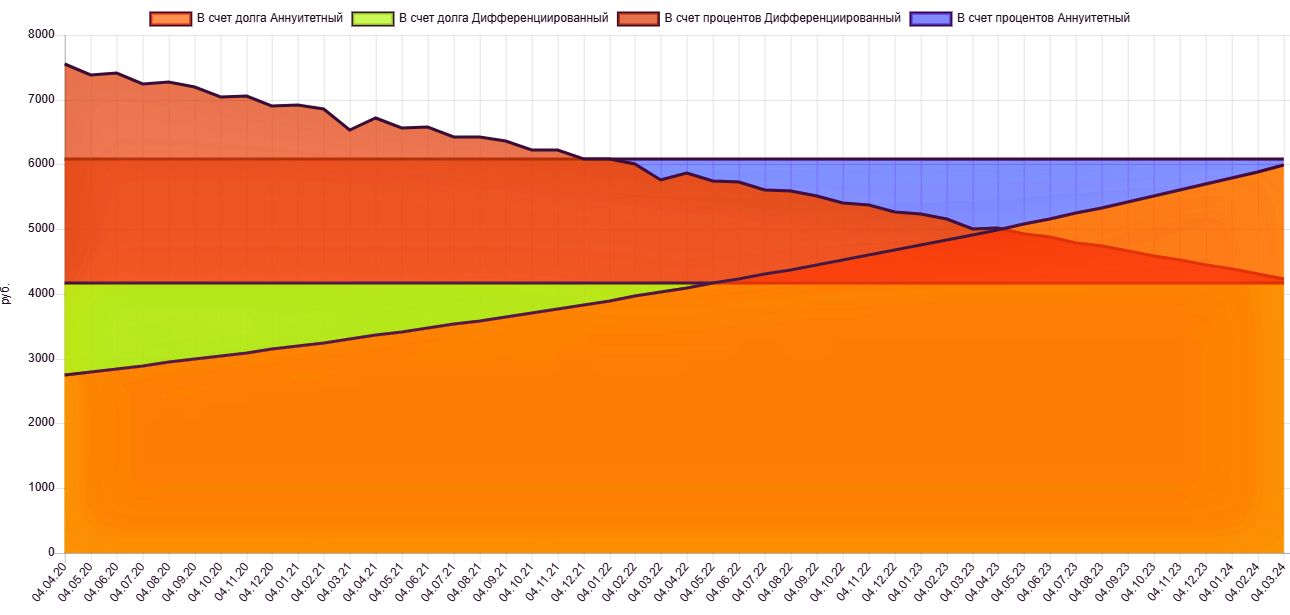
Рис. 10 – Наложение двух графиков
Дело в том, что в дифференцированной схеме проценты начисляются на ОСТАТОК долга, а в аннуитетной схеме часть долга переходит на конец кредитного срока. Значит остаток больше, чем в дифференцированной схеме.