ОП.05. Основы гидравлики и теплотехники
Урока)
Гр. 5. Основы гидравлики и теплотехники
Преподаватель: Рыжонкова С.А.
Адрес электронной почты: ryzhonkovasvetlana@yandex.ru
Тема: Практическое занятие № 9 по теме: Истечение жидкости через отверстия
Цель: Изучитьистечение жидкости через отверстия
Форма работы: индивидуальная, дистанционное обучение
Тип урока: Практическое занятие (2 урока)
Обеспечение занятий: калькулятор, линейки, карандаши, ручки, рабочая тетрадь.
Место проведения: индивидуальное, электронное обучение
Время проведения: 2 часа, (2 урока).
Практическая часть:
1. Истечение жидкости через малое отверстие в тонкой стенке при постоянном напоре
2. Распределение скоростей по сечению струи
3. Истечение жидкости, когда стенки сосуда удалены от отверстия на расстояние
4. Истечение жидкости через круглое отверстие
5. Истечение жидкости через затопленное отверстие при постоянном напоре
Методические указания к практической работе описание самой работы
1. Записать, для чего предназначены отверстия и насадки
2. Перечислить виды отверстий для истечения жидкости
3. Ответить на контрольные вопросы
Краткие теоретические сведения
Истечение жидкости через малое отверстие в тонкой стенке при постоянном напоре
Отверстия и насадки, через которые вытекает жидкость, предназначены для определенных практических целей. В зависимости от назначения им придают соответствующую форму. При рассмотрении истечения жидкости через отверстия и насадки основным вопросом является определение скорости истечения и расхода жидкости для различных форм отверстий и насадок.
Малым отверстием называется такое отверстие, вертикальный размер которого мал по сравнению с напором Н (не превышает 1/10) и размерами резервуара. В этом случае давление во всех точках отверстия может считаться одинаковым и равным давлению в центре тяжести отверстия.
|
|
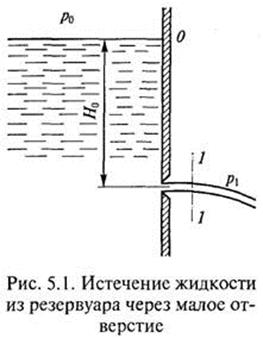
Возьмем резервуар, заполненный жидкостью. Стенки резервуара считаем тонкими, жидкость вытекает через отверстие в стенке резервуара (рис. 5.1).
Отверстием в тонкой стенке называется отверстие с фаской или с заостренными кромками в стенке, толщина которой не влияет на условия истечения и форму струи. Отверстие расположено на расстоянии Hо от свободной поверхности жидкости. Считаем Hо = const. Поскольку истечение жидкости будет происходить при постоянном напоре Но, то движение ее будет установившимся. Следовательно, можно применить уравнение Бернулли, рассматривая — одно сечение в резервуаре, другое – в струе. Отсчет ведем от центра отверстия. Уравнение примет вид
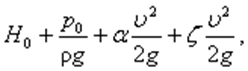
где α — коэффициент Кориолиса; ζ – коэффициент сопротивления отверстия.
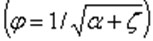Истечение жидкости будет определяться разностью давлений жидкости по обе стороны отверстия.
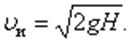где φ — коэффициент скорости. Для идеальной жидкости ζ = 0, α = 1, следовательно,
Таким образом, коэффициент скорости φ есть отношение действительной скорости истечения υ к скорости истечения идеальной жидкости υи, т. е. φ = υ/υи.
Распределение скоростей по сечению струи (рис. 5.2) является равномерным только в ядре струи, т. е. в средней части сечения, наружный слой жидкости имеет меньшую скорость в результате трения о стенку. Поэтому φ является коэффициентом средней скорости. При истечении жидкости через отверстие струя жидкости отрывается от стенки у кромки отверстия и затем сжимается. Сжатие обусловлено тем, что частицы жидкости, подходящие к отверстию вдоль стенки, не могут сразу повернуть на 90°, а огибают кромки отверстия по некоторой кривой. Крайние струйки придают вытекающей струе коноидальную форму. В зависимости от расположения отверстия.
|
|
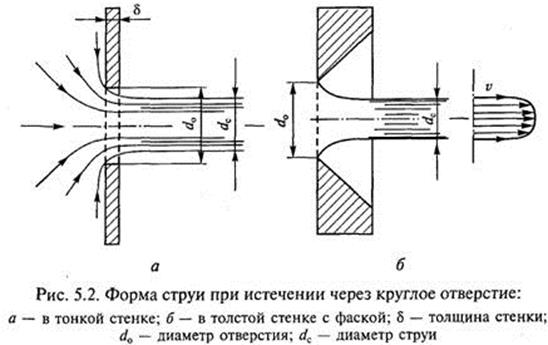
сжатие вытекающей струи будет различным. Наибольшее сжатие струи наблюдается на расстоянии от стенки около 0,5 dо, где dо — диаметр отверстия.
Если стенки сосуда удалены от отверстия на расстояние l ≥ 3 d (рис. 5.3, а), то они не оказывают влияния на сжатие струи. Струя испытывает сжатие со всех сторон. Такое сжатие называется полным и совершенным. Если отверстие находится вблизи стенок (нижнее на рис. 5.3, а), то они оказывают влияние на сжатие струи. Площадь сжатого сечения за отверстием будет больше, чем при совершенном сжатии. Такое сжатие называется полным и несовершенным. При неполном и несовершенном сжатии струя испытывает сжатие не по всему периметру отверстия (рис. 5.3, б). Степень сжатия оценивается коэффициентом сжатия е, равным отношению площади поперечного сечения струи к площади отверстия: ε = ωс/ωо; при круглом отверстии ε = dс/dо. Площадь поперечного сечения струи ωс = εωо, сжатие вытекающей струи будет различным. Наибольшее сжатие струи наблюдается на расстоянии от стенки около 0,5dо, где dо — диаметр отверстия.
|
|
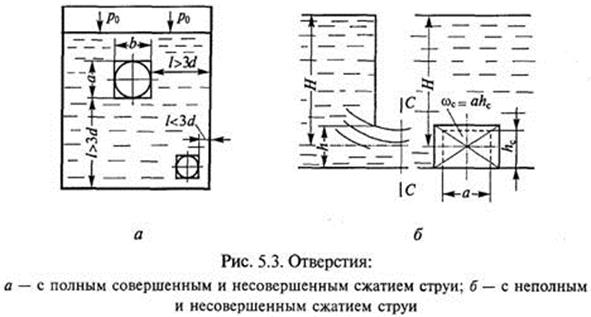
При истечении жидкости через круглое отверстие струя принимает цилиндрическую форму на расстоянии от кромки отверстия, равном его диаметру. Расход жидкости, истекающей через отверстие, определяется действительной скоростью жидкости и фактической площадью сечения струи:
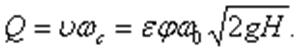
Произведение εφ = μ называется коэффициентом расхода.
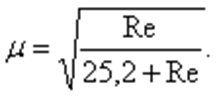Коэффициенты ε, φ и μ, зависящие от типа отверстия или насадки и от числа Re определяются экспериментально. При очень малых числах Рейнольдса (Re < 25) на коэффициенты скорости и расхода существенное влияние оказывает вязкость. Торможение жидкости у кромки отверстия становится столь значительным, что сжатия струи не происходит, т. е. ε = 1 и φ = μ. В этом случае для определения коэффициента расхода можно пользоваться формулой