Исследование эффективности робастных моделей для представления детерминированных функционалов
Цель работы
1. Углубить и закрепить знания по теории нечеткого логического вывода.
2. Исследовать возможности нечетких моделей логического вывода для аппроксимации сложных детерминированных функционалов (идентификации нелинейных зависимостей).
Краткие теоретические сведения
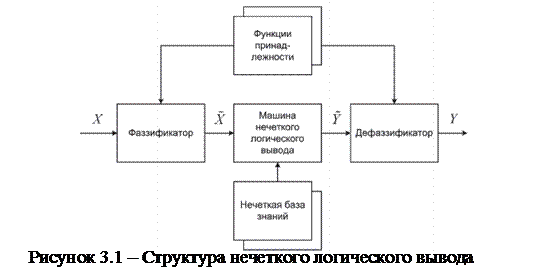
Нечеткий логический вывод—это аппроксимация зависимости «входы–выход» на основе лингвистических высказываний типа «ЕСЛИ–ТО» и операций над нечеткими множествами. Основные положения теории нечетких множеств, используемые в настоящей статье, приведены в Приложении1. Типовая структура модели на основе нечеткого логического вывода (которую в дальнейшей будем называть нечеткой моделью) показана на рис. 5.1. Нечеткая модель содержит следующие блоки:
- фаззификатор, преобразующий фиксированный вектор влияющих факторов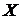 
в вектор нечетких множеств 
, необходимых для выполнения нечеткого логического вывода;
- нечеткая база знаний, содержащая информацию о зависимости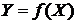 
в виде лингвистических правил типа «ЕСЛИ–ТО»;
- машина нечеткого логического вывода, которая на основе правил базы знаний определяет значение выходной переменной в виде нечеткого множества 
, соответствующего нечетким значениям входных переменных ;
- дефаззификатор, преобразующий выходное нечеткое множество в четкое число 
.
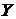В пакете Fuzzy Logic Toolbox (Matlab) реализованы два типа нечетких моделей: типа Мамдани и типа Сугено. Эти модели отличаются форматом базы знаний и процедурой дефаззификации.
Нечеткая модель типа Мамдани
В модели типа Мамдани взаимосвязь между входами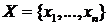 
и выходом 
определяется нечеткой базой знаний формата:
|
|
ЕСЛ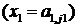И 
И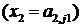 
И…. ИЛИ 
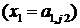И 
И … ТО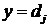 
, 
. Здесь 
- лингвистический терм, которым оценивается переменная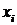 
в строке с номером 
, 
, 
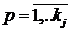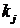- количество строк конъюнкций, в которых выход оценивается лингвистическим термом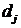 
, 
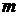- количество термов, используемых для лингвистической оценки выходной переменной . Иначе базу знаний можно представить как:
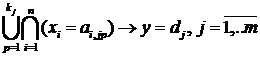(5.1)
Все лингвистические термы в базе знаний (3.1) представляются как нечеткие множества, заданные соответствующими функциями принадлежности.
Нечеткая база знаний (3.1) может трактоваться как некоторое разбиение пространства влияющих факторов на подобласти с размытыми границами, в каждой из которых функция отклика принимает значение, заданное соответствующим нечетким множеством. Правило в базе знаний представляет собой «информационный сгусток», отражающий одну из особенностей зависимости «входы-выход». Такие «сгустки» могут рассматриваться как аналог вербального кодирования, которое аналогично процессу обучения, протекающему в человеческом мозге.
Пусть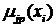 
- функция принадлежности входа 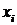нечеткому терму , 
, 
, 
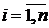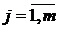, т.е.
(3.2)
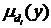- функция принадлежности выхода нечеткому терму 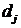, , 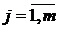т.е.
(3.3)
Степень принадлежности входного вектора 
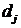нечетким термам из базы знаний (3.1) определяется следующей системой нечетких логических уравнений:
(3.4)
где 
- операция s-нормы (максимум, или «логическое ИЛИ»), а 
- операция t-нормы (минимум, или логическое «И»).
Нечеткое множество 
, соответствующее входному вектору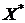 
, определяется следующим образом:
, (3.5)
где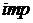 
- операция импликации (реализуется как нахождение минимума), 
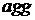- операция агрегирования (реализуется как операция максимума).
|
|
Четкое значение , соответствующее входному вектору 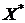, определяется в результате дефазификации нечеткого множества по методу «центра тяжести»:
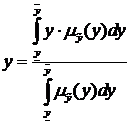(3.6)