Фирма постоянно поставляет на рынок новинки видеозаписей. Себестоимость одного диска (диск, работа, лицензионные отчисления) равна C=140 рублей. В первую неделю продаж диск позиционируется как новинка и продается в собственном магазине по цене P=200 руб. за штуку. Со второй недели цена дисков резко падает и они передаются в торговые сети по остаточной стоимости 40 руб. за диск. Директор фирмы знает, что за первую неделю возможно продать от 2 до 4 коробок с дисками по 500 штук в каждой. Вероятность спроса равна 30% для 2 коробок, 50% для 3 коробок и 20% для 4 коробок. Если сделать скидку на диски, равную D=3 %, то вероятность спроса поменяется и будет равна 20% для 2 коробок, 40% для 3 коробок и 40% для 4 коробок.
1. Определить оптимальную стратегию поведения фирмы для оптимизации прибыли. Имеет ли смысл делать скидку на фильмы?
2. Определить, какова максимальная стоимость информации о реальном спросе на конкретную видеозапись? Имеет ли смысл делать скидку в этом случае?
Подсказка: предложения со скидкой и без нее рассмотреть как отдельные возможные стратегии статистика с зависящими от них вероятностями состояний природы.
Решение:
1. Определим оптимальную стратегию поведения фирмы без скидок.
Запишем матрицу игры с природой для этой задачи. Выигрышем будем считать прибыль, которую получит фирма в каждой ситуации.
Строки матрицы будут соответствовать возможным стратегиям фирмы – продавать в собственном магазине 2, 3 или 4 коробки дисков.
Столбцы будут соответствовать спросу на диски: 2, 3 или 4 коробки.
Матрицу игры с природой представим в таблице
| Спрос Предложение | 2 коробки | 3 коробки | 4 коробки |
| 2 коробки | =2*500*(200-140) | =2*500*(200-140) | =2*500*(200-140) |
| 3 коробки | =2*500*(200-140)+1*500*(40-75) | =3*500*(200-140) | =3*500*(200-140) |
| 4 коробки | =2*500*(200-140)+2*500*(40-140) | =3*500*(200-140)+1*500*(40-140) | =4*500*(200-140) |
Вероятности 
| 0,3 | 0,5 | 0,2 |
Тогда получим платежную матрицу:
| Спрос Предложение | 2коробки | 3 коробки | 4 коробки |
| 2 коробки | |||
| 3 коробки | |||
| 4 коробки | -40000 | ||
| Вероятности
| 0,3 | 0,5 | 0,2 |
Поскольку заданы вероятности спроса, то для выбора стратегии применяем критерий Байеса.
В1=0,3*60 000+0,5*60 000+0,2*60 000=60000
В2=0,3*42500+0,5*90 000+0,2*90 000=75750
В3=0,3*(-40000)+0,5*40000+0,2*120000=32000
Вопт=max(60000; 75750; 32000) =75750= В2
C2→ Thebest (Bayes)
Таким образом, лучше продавать в собственном магазине 3 коробки дисков. Тогда средняя прибыль от продажи составит 75750рублей.
Определим оптимальную стратегию поведения фирмы с учетом скидок. Запишем матрицу игры с природой для этой задачи.
| Спрос Предложение | 2 коробки | 3 коробки | 4 коробки |
| 2 коробки | =2*500*(200*0,97-140) | =2*500*(200*0,97-140) | =2*500*(200*0,97-140) |
| 3 коробки | =2*500*(200*0,97-140)+1*500*(40-140) | =3*500*(200*0,97-140) | =3*500*(200*0,97-140) |
| 4 коробки | =2*500*(200*0,97-140)+2*500*(40-140) | =3*500*(200*0,97-140)+1*500*(40-140) | =4*500*(200*0,97-140) |
| Вероятности
| 0,2 | 0,4 | 0,4 |
Тогда получим платежную матрицу:
| Спрос Предложение | 2коробки | 3 коробки | 4 коробки |
| 2 коробки | |||
| 3 коробки | |||
| 4 коробки | -46000 | ||
| Вероятности
| 0,2 | 0,4 | 0,4 |
В1=0,2*54000+0,4*54000+0,4*54000=54000
В2=0,2*4000+0,4*81000+0,4*81000=65600
В3=0,2*(-46000)+0,4*31000+0,4*108000=46400
Вопт=max(54000; 65600; 46400) =65600= В2
C2→ The best (Bayes)
Таким образом, с учетом скидок лучше продавать в собственном магазине 3 коробки дисков. Тогда средняя прибыль от продажи составит 65600рублей.
Так как при скидках ожидаемая средняя прибыль ниже на 10150рублей, то не стоит делать скидки.
2. Если фирма будет точно знать спрос на фильмы, то будет продавать в своем магазине столько, сколько спрос. Тогда средняя прибыль составит:
без скидки В=(60000+90000+120000)/3=90000
со скидкой В=(54000+81000+108000)/3=81000
Значит, в этом случае скидку делать не стоит.
Имея информацию о спросе, фирма может увеличить среднюю прибыль на
90000-75750= 14250рублей,
это и есть стоимость информации о реальном спросе на конкретную видеозапись.
ТЕМА 2.
Управление запасами.
Детерминированные модели
Объем продаж магазина «Ткани» составляет v= 520 рулонов в год. Величина спроса равномерно распределяется в течение года (365 дней). Цена закупки одного рулона равна C=140 тыс. руб. За доставку и оформление заказа владелец магазина должен заплатить K = 28 тыс. руб. Время доставки заказа от поставщика составляет t д = 6 дней. Издержки хранения составляют s= 60 руб. в день за один рулон. Необходимо определить: сколько рулонов ткани должен заказывать владелец магазина для одной поставки, частоту заказов, точку заказа и минимальные суммарные затраты за период времени T= 5 года.
1. Рассмотреть случай поставок без скидок.
2. Определить оптимальные параметры работы системы управления запасов при следующих скидках:
| Размер заказа | Цена, тыс. руб./шт. |
| От 1 до(Q1-1)=17 | скидки нет |
| От Q1= 18до(Q2-1)=83 | P1=7 % |
| От Q2=84и более | P2=12% |
Следует ли владельцу магазина воспользоваться одной из скидок, предоставляемых поставщиком? Каковы при этом будут размер заказа и общие затраты на управление запасами?
Решение:
Определяем входящие параметры системы.
К= 28тыс.руб.;
v = 520рул./12мес.=43,3рул./мес.;
Т =5 лет = 60мес;
s =60 руб./рул.день= 1,8тыс.руб./рул.мес.
tд =6 дней=0,2 мес.
В первой части задачи:
С =140тыс.руб
Во второй части задачи:
Q1=18рул.,
Q2=84рул.,
С0=140 тыс. руб.,
С1=130,2 тыс. руб.,
С2=123,2 тыс. руб.
1. Определим оптимальные параметры функционирования системы УЗ без скидок:
рул.
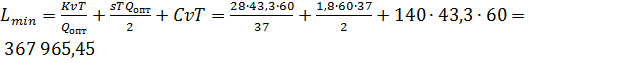тыс.руб.
поставок за 60 месяцев.
поставок в месяц.
мес.≈25 дней.
рулонов.
Вывод: при отсутствии скидок необходимо организовать поставки примерно по 37рулону каждые 25 дней. Заказ необходимо делать в момент, когда в наличии осталось 9 рулонов. Суммарные расходы на поставку и хранение рулонов ткани составят 367965,45тыс.рублей за 5 лет.
2. Для решения 2 части задачи необходимо найти Q* по формуле Уилсона и определить затраты без скидки при этом объеме. Это уже сделано в первой части задачи: Q* =37, L* =367965,45тыс.руб.
Рассмотрим сначала задачу с первой скидкой. Так как Q*>Q1 , то найдем L1 по формуле:
тыс.руб.
Рассмотрим задачу со второй скидкой. Так как Q*<Q2 , то найдем L2 по формуле:
тыс.руб.
Наименьшее из значений расходов равно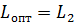 
.
Тогда 
рулона.
Остальные параметры находим по формулам:
поставки за 5лет.
поставки в месяц.
мес. = 58 дней.
рулонов.
Вывод: при имеющейся системе скидок выгодно пользоваться второй скидкой. Необходимо организовать поставки по 84 рулонов примерно каждые 58 дней. Заказ необходимо делать в момент, когда в наличии осталось 9 рулона. Суммарные расходы на поставку и хранение рулонов ткани составят примерно 325 722,67тыс. рублей за 5 лет.
ТЕМА 3.
КРИТЕРИАЛЬНЫЕ МЕТОДЫПРИНЯТИЯ РЕШЕНИЙ
Вы, – руководитель и совладелец крупной организации, – планируете вложение прибыли в социальный проект для сотрудников. Рассматриваются 4 возможных проекта:
· спортзал;
· дополнительное медицинское страхование;
· парк отдыха для сотрудников и их детей;
·??? – предложите свой вариант.
Важнейших критериев для данных проектов три:
· стоимость;
· массовость охвата сотрудников;
· укрепление корпоративного духа.
Задание
Определить, используя метод Саати, лучший вариант социального проекта для Вашей организации. Принять управленческое решение.
При выполнении задания все сравнения (кроме заданных по вариантам в таблицах З1 и З2) проведите на свое усмотрение, оставаясь в рамках здравого смысла и не противоречащие друг другу.
Таблица З1. Фиксированные сравнения критериев по цели
| ВАРИАНТ | СРАВНЕНИЕ КРИТЕРИЕВ |
| Корпоративный дух и стоимость равноценны |
Таблица З2. Фиксированные сравнения альтернатив по критериям
| ВАРИАНТ | СРАВНЕНИЕ КРИТЕРИЕВ |
| Спортзал по стоимости немного дороже чем парк отдыха |
Подсказка: по стоимости дороже – это хуже, дешевле – лучше.
Решение:
1. Выделение проблемы. Определение цели.
Цель – социальный проект для сотрудников.
2. Выделение основных критериев, обуславливающих достижение цели:
· стоимость;
· массовость охвата сотрудников;
· укрепление корпоративного духа.
3. Выделение группы альтернатив, представляющих наибольший интерес.
· спортзал;
· дополнительное медицинское страхование;
· парк отдыха для сотрудников и их детей;
· проведение тренига.
4. Построение иерархии: дерево от цели через критерии к альтернативам.
Дерево иерархии представлено на рис. 1.
 |
Рис. 2. Дерево иерархии
5. Построение матрицы попарных сравнений критериев по цели.
· Корпоративный дух и стоимость равноценны.
· Спортзал по стоимости немного дороже, чем парк отдыха
Составляется таблица качественного сравнения критериев (табл. 3).сравнения взаимны, то достаточно составить только ее часть, расположенную над главной диагональю:
Таблица 3. Качественное сравнение критериев
| Стоимость | Массовость охвата сотрудников | Укрепление корпоративного духа | |
| Стоимость | Немного важнее | равноценны | |
| Массовость охвата сотрудников | Менее важнее | ||
| Укрепление корпоративного духа | немного важнее |
На основе таблицы качественного сравнения по таблице 3 строится таблица – матрица баллов (табл. 4). Под главной диагональю записываются числа, обратные к соответствующим числам над диагональю. На диагонали всегда ставятся единицы.
Таблица 3. Количественные баллы сравнения критериев
| Стоимость | Массовость охвата сотрудников | Укрепление корпоративного духа | |
| Стоимость | |||
| Массовость охвата сотрудников | 1/3 | 1/5 | |
| Укрепление корпоративного духа |
6. Построение матриц попарных сравнений альтернатив по критериям.
Опустим подробное изложение всех операций и приведем ниже только матрицы количественных баллов (табл. 4 – 6):
Таблица 4. Количественные баллы сравнения альтернатив по стоимости
| спортзал | дополнительное медицинское страхование | парк отдыха для сотрудников и их детей | Тренинг | |
| спортзал | 1/3 | 1/3 | ||
| дополнительное медицинское страхование | ||||
| парк отдыха для сотрудников и их детей | 1/8 | 1/3 | ||
| Тренинг | 1/5 | 1/5 |
Таблица 5. Количественные баллы сравнения альтернатив
по массовости охвата сотрудников
| спортзал | дополнительное медицинское страхование | парк отдыха для сотрудников и их детей | Тренинг | |
| спортзал | 1/8 | 1/5 | 1/8 | |
| дополнительное медицинское страхование | 1/3 | |||
| парк отдыха для сотрудников и их детей | 1/5 | 1/3 | ||
| Тренинг |
Таблица 6. Количественные баллы сравнения альтернатив
по укреплению корпоративного духа
| спортзал | дополнительное медицинское страхование | парк отдыха для сотрудников и их детей | Тренинг | |
| спортзал | ||||
| дополнительное медицинское страхование | 1/5 | 1/5 | 1/3 | |
| парк отдыха для сотрудников и их детей | ||||
| Тренинг | 1/5 | 1/8 |
7. Применение методики анализа полученных матриц
Таблица 7. Определение сумм столбцов матрицы 3
| Стоимость | Массовость охвата сотрудников | Укрепление корпоративного духа | |
| Стоимость | 1,000 | 3,000 | 1,000 |
| Массовость охвата сотрудников | 0,333 | 1,000 | 0,200 |
| Укрепление корпоративного духа | 3,000 | 5,000 | 1,000 |
| Сумма | 4,333 | 9,000 | 2,200 |
Таблица 8. Деление элементов на сумму соответствующего столбца и определение средних значений по строкам
| Стоимость | Массовость охвата сотрудников | Укрепление корпоративного духа | Срзнач | |
| Стоимость | 0,231 | 0,333 | 0,455 | 0,340 |
| Массовость охвата сотрудников | 0,077 | 0,111 | 0,091 | 0,093 |
| Укрепление корпоративного духа | 0,692 | 0,556 | 0,455 | 0,567 |
Полученный в итоге столбец задает веса строк матрицы, – в данном случае – веса критериев с точки зрения поставленной цели.
Этот столбец называют весовым столбцом критериев по цели (см. табл. 9).
Таблица 9. Весовой столбец критериев по цели
| Вес в долях | Вес в процентах | |
| Стоимость | 0,340 | 34,0% |
| Массовость охвата сотрудников | 0,093 | 9,3% |
| Укрепление корпоративного духа | 0,567 | 56,7% |
Промежуточные выводы: С точки зрения удовлетворения нашей цели наиболее весомым является укрепление корпоративного духа (56,7%), далее следует стоимость (34%). Массовость охвата сотрудников имеет наименьший весовой коэффициент в 9,3%.
Данные действия повторяем для всех матриц попарного сравнения альтернатив по критериям. Получаем следующие результаты (табл. 10 – 12):
Таблица 10. Весовой столбец альтернатив по стоимости
| Вес в долях | Вес в процентах | |
| спортзал | 0,202 | 20,2% |
| дополнительное медицинское страхование | 0,527 | 52,7% |
| парк отдыха для сотрудников и их детей | 0,151 | 15,1% |
| тренинг | 0,120 | 12,0% |
Таблица 11. Весовой столбец альтернатив по массовости охвата
| Вес в долях | Вес в процентах | |
| спортзал | 0,041 | 4,1% |
| дополнительное медицинское страхование | 0,331 | 33,1% |
| парк отдыха для сотрудников и их детей | 0,142 | 14,2% |
| тренинг | 0,485 | 48,5% |
Таблица 12. Весовой столбец альтернатив
по укреплению корпоративного духа
| Вес в долях | Вес в процентах | |
| спортзал | 0,352 | 35,2% |
| дополнительное медицинское страхование | 0,059 | 5,9% |
| парк отдыха для сотрудников и их детей | 0,404 | 40,4% |
| тренинг | 0,185 | 18,5% |
8. Определение весов альтернатив по системе иерархии.
8.1. Столбцы весов в долях альтернатив по критериям объединяем в общую матрицу весов альтернатив по всем критериям (табл. 13).
Таблица 13. Матрица весов альтернатив по всем критериям
| Стоимость | Массовость охвата сотрудников | Укрепление корпоративного духа | |
| спортзал | 0,527 | 0,331 | 0,059 |
| дополнительное медицинское страхование | 0,151 | 0,142 | 0,404 |
| парк отдыха для сотрудников и их детей | 0,120 | 0,485 | 0,185 |
| Тренинг | 0,527 | 0,331 | 0,059 |
8.2. Умножаем полученную матрицу на столбец весов критериев по цели матрично (по правилу строка на столбец):
В результате получаем веса альтернатив с точки зрения достижения поставленной цели (табл. 14). Как следует из таблицы, парк отдыха для сотрудников и их детей является наиболее привлекательным для поставленной цели. Если же мы будем выполнять два проекта, то это будут проекты: парк отдыха для сотрудников и их детей и спортзал.
Таблица 14. Матрица веса альтернатив с точки зрения достижения поставленной цели
| Вес в долях | Вес в процентах | |
| спортзал | 0,272 | 27,2% |
| дополнительное медицинское страхование | 0,243 | 24,3% |
| парк отдыха для сотрудников и их детей | 0,294 | 29,4% |
| Тренинг | 0,191 | 19,1% |