ЗАДАНИЕ 3. КАНАЛЫ РАДИОСВЯЗИ

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Гражданской авиации

Кафедра радиотехнических устройств

 

КурсовАЯ РАБОТА

по дисциплине

ЭЛЕКТРОДИНАМИКА

И

РАСПРОСТРАНЕНИЕ

РАДИОВОЛН

 

Тема: расчет направляющих структур ЭМВ и РРВ

по естественным трассам

 

 

	Выполнила: студентка IV курса
	факультета ПМиВТ а группы БИ-4-1 м
	Ершова Л.
	шифр 090106 а
	Руководитель: профессор Яманов Д.Н.
	Защищена с оценкой в «»20 г.__а

 

Москва -2013

 

 

СОДЕРЖАНИЕ

 

ЗАДАНИЕ 1. ЛИНИИ ПЕРЕДАЧИ ВЫСОКОЧАСТОТНОГО ДИАПАЗОНА∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙2

 

ЗАДАНИЕ 2. ОБЪЁМНЫЕ РЕЗОНАТОРЫ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙13

 

ЗАДАНИЕ 3. КАНАЛЫРАДИОСВЯЗИ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙17

 

СПИСОК ЛИТЕРАТУРЫ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙21

 

ПРИЛОЖЕНИЕ 1∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙22

 

ПРИЛОЖЕНИЕ 2∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙23

 

ПРИЛОЖЕНИЕ 3∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙24

 

ПРИЛОЖЕНИЕ 4∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙25

 

 

 

ЗАДАНИЕ 1. ЛИНИИ ПЕРЕДАЧИ ВЫСОКОЧАСТОТНОГО ДИАПАЗОНА

1.1.Техническое задание

 

1. Выбрать поперечные размеры прямоугольного волновода по заданным рабочим частотам и по минимальной частоте у круглого волновода. Стандарт на волноводы приведен в приложении 2.

2. Найти значения K_x, K_y, K_z (прямоугольный волновод) и g_Е,Н , K_z (круглый волновод) – на λ_ср.

3. Используя найденные в п.2 значения K, записать выражения для полей заданного типа волны.

4. Найти поперечные размеры волновода при работе с высшими типами

волн (при заданной рабочей волне H₁₀ – найти размеры для волны H₂₀; при работе с волной H₁₁ в круглом волноводе найти диаметр под волну E₀₁, а при работе с высшей волной E₀₁, найти диаметр для волны H₁₁). Показать, в каком случае поперечные размеры получаются меньше – при работе с основной или с высшей волной.

5. Найти критическую частоту и критическую длину волны заданного типа.

6. Найти длину волны в волноводе, фазовую и групповую скорости на

средней длине волны.

7. Найти максимально допустимую длину волновода, при которой не наблюдалось бы заметных искажений формы сигнала при работе короткими импульсами высокой частоты f_макс и длительностьюτ =10^-7 с.

8. Рассчитать предельную мощность в волноводе на средней частоте при

выбранных его стандартных размерах. Найти пробивную мощность при

КСВ = 1,2, максимально допустимую мощность и сравнить ее с рабочей мощностью.

9. Найти коэффициент затухания на средней частоте.

10. Найти отношение амплитуд поля (при x = const и y = const) и мощностей на расстоянии l, м при рассчитанной величине коэффициента затухания.

11. Определить, на каком расстоянии амплитуды поля волн H₂₀ в прямоугольном и H₀₁ в круглом волноводах (исходя из задания), находящихся в закритическом режиме, уменьшаются не менее чем в сто раз, если частота равна средней частоте диапазона (надо предварительно найти λ_кр волны H₂₀ или H₀₁).

12. Найти КПД несогласованной с нагрузкой линии передачи при длине линии l и КБВ = 0,8.

 

 

 

1.2. Данные для расчета задания 1:

Полоса рабочих частот - ∆ƒ= 11–12, ГГц;

Напряженность поля - Е= 20, В/м;

Удельная объёмная проводимость - γ = 2∙10⁷, 1/Ом∙м;

Длина линии l = 2, м;

Тип волны Н₁₀;

Форма сечения волновода – прямоугольная;

Длительность импульса τ = 10^-7, с;

Пробивная напряженность Е_проб=3, кВ/мм;

КБВ = 0,8;

КСВ = 1,2.

 

1.3. Расчёты по п. 1-12 задания №1

 

1.3.1. Вы­бираем по­пе­реч­ные раз­ме­ры пря­мо­уголь­но­го вол­но­во­да по за­дан­ным ра­бо­чим час­то­там.

Пред­ва­ри­тель­но най­дем дли­ны волн ра­бо­че­го диа­па­зо­на:

 

; ,

 

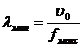где - так как вол­но­вод за­пол­нен воз­ду­хо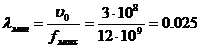м.

, м,

, м.

 

 

 

Так как в данном варианте используется прямоугольный волновод и волна типа Н₁₀, то ус­ло­вие для вы­бо­ра размеров волновода:

0.9 λ_мин а 0.6 λ_мах; b а / 2.

В данном случае получаем:

22.5 мм а 16.32 мм.

Получив данные неравенства, выбираем волновод типа R120 из приложения 2, параметры которого: ∆ƒ=9.84–15.0 ГГц; a=19.05 мм; b=9.52 мм.

 

 

1.3.2. Най­дём зна­че­ния K_x, K_y, K_z.

Для пря­мо­уголь­но­го вол­но­во­да зна­че­ния Кx и Кy рав­ны:

; ,

где m, n – ин­дек­сы, ко­то­рые ста­вят­ся око­ло на­зва­ния вол­ны (Н_mn где m = 0,1,2,3…; n = 0,1,2,3…).

, рад/м,

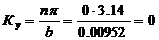, рад/м.

Ко­эф­фи­ци­ент фа­зы в вол­но­во­де

,

 

где - для пря­мо­уголь­но­го вол­но­во­да;

и – так как ди­элек­три­ком слу­жит воз­дух;

 

Получаем , так как, К_у=0

рад/м.

 

 

 

1.3.3. За­пи­сать вы­ра­же­ние для по­ля за­дан­но­го ти­па вол­ны.

 

Для пря­мо­уголь­но­го вол­но­во­да из ре­ше­ния урав­не­ний Мак­свел­ла с вы­пол­не­ни­ем гра­нич­ных ус­ло­вий на иде­аль­но про­во­дя­щих стен­ках полу­ча­ют­ся ре­ше­ния для ком­плекс­ных ам­пли­туд по­ля волн ти­па Н_mn:

;

;

;

;

;

где ;

;

– на­чаль­ная фа­за на­пря­жен­но­сти маг­нит­но­го по­ля, рад;

– дей­ст­ви­тель­ная ам­пли­ту­да на­пря­жен­но­сти про­доль­но­го магнитно­го по­ля, А/м;

, –ком­плекс­ные ам­пли­ту­ды на­пря­жен­но­сти элек­три­че­ско­го по­ля, В/м.

, А/м;

, А/м;

, А/м;

, В/м;

, В/м;

 

 

 

1.3.4. Най­ти по­пе­реч­ные раз­ме­ры вол­но­во­да при ра­бо­те с выс­ши­ми ти­па­ми волн (при за­дан­ной ра­бо­чей вол­не H₁₀ – най­ти раз­ме­ры для вол­ны H₂₀). По­ка­зать, в ка­ком слу­чае по­пе­реч­ные раз­ме­ры по­лу­ча­ют­ся мень­ше – при ра­бо­те с ос­нов­ной или с выс­шей вол­ной.

 

Критическая длина волны в волноводе:

 

Для H₂₀ -

 

 

1.3.5. Най­ти кри­ти­че­скую час­то­ту и кри­ти­че­скую дли­ну вол­ны заданного ти­па.

 

В прямоугольном волноводе критическая частота волны типа Н10 равна:

 

,

 

где – так как волновод заполнен воздухом.

 

, рад/с;

, м.

 

1.3.6. Найдём дли­ну вол­ны в вол­но­во­де, фа­зо­вую и груп­по­вую ско­ро­сти на сред­ней дли­не вол­ны.

Длина волны в волноводе, фазовая и групповая скорости вычисляются для прямоугольного волновода по формулам:

 

,

, м;

 

;

 

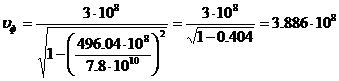, м/с;

,

 

где .

, м/с.

 

 

1.3.7. Най­ти мак­си­маль­но до­пус­ти­мую дли­ну вол­но­во­да, при ко­то­рой не на­блю­да­лось бы заметных ис­ка­же­ний фор­мы сиг­на­ла при ра­бо­те ко­рот­ки­ми им­пульса­ми вы­со­кой час­то­ты и дли­тель­но­стью с.

Максимально допустимая длина волновода, при которой искажения еще невелики

 

,

где - разность двух крайних частот спектра.

=7.89, ГГц; , Гц;

, м;

м.

1.3.8. Рас­счи­тать пре­дель­ную мощ­ность в вол­но­во­де на сред­ней час­то­те при вы­бран­ных его стан­дарт­ных раз­ме­рах. Най­ти про­бив­ную мощ­ность при КСВ = 1,2, мак­си­маль­но до­пус­ти­мую мощ­ность и срав­нить ее с ра­бо­чей мощ­но­стью.

 

Предельная мощность в прямоугольном волноводе на средней частоте и волне типа Н₁₀:

 

.

, Вт.

Пробивная мощность / КСВ,

где КСВ – коэффициент стоячей волны.

 

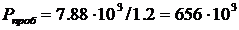, Вт.

 

Максимально допустимая мощность

.

Вт.

Рабочая мощность (мощность, проходящая по волноводу)

;

Вт.

где – амплитуда максимального значения электрического поля.

В задании именно это максимальное значение поля задано.

 

Проверим, выполняется ли условие << .

 

Вт << Вт

Условие выполняется.

 

1.3.9. Най­ти ко­эф­фи­ци­ент за­ту­ха­ния на сред­ней час­то­те.

Коэффициент затухания волн типа Н₁₀ в прямоугольном волноводе при воздушном заполнении равен

, дБ/м,

где – удельное поверхностное сопротивление

, Ом,

где g - удельная объемная проводимость стенок.

, Ом;

 

 

 

 

, дБ/м.

1.3.10. Най­ти от­но­ше­ние ам­пли­туд по­ля (при x = const и y = const) и мощ­но­стей на рас­стоя­нии l м при рас­счи­тан­ной ве­ли­чи­не ко­эф­фи­ци­ен­та за­ту­ха­ния.

Отношение амплитуд поля и отношение мощностей можно найти из следующей формулы

 

, дБ/м;

 

1.3.11. Оп­ре­де­лить, на каком рас­стоя­нии ам­пли­ту­ды по­ля вол­н H₂₀ в пря­мо­уголь­ном, на­хо­дя­щих­ся в зак­ри­ти­че­ском ре­жи­ме, умень­ша­ют­ся не ме­нее чем в сто раз, ес­ли час­то­та рав­на сред­ней час­то­те диа­па­зо­на (на­до пред­ва­ри­тель­но най­ти вол­ны H₂₀).

Расстояние , на котором поле волны , находящейся в закритическом режиме, уменьшается в 100 раз на средней частоте диапазона, находится так:

 

;

.

 

 

 

Критическая длина волны типа при выбранных размерах прямоугольного волновода

, м.

Коэффициент закритического затухания ,

где - для воздуха.

, рад/м.

Откуда расстояние, на котором поле уменьшится в 100 раз, равно

, м.

1.3.12. Най­ти КПД не­со­гла­со­ван­ной с на­груз­кой ли­нии пе­ре­да­чи при дли­не ли­нии l и КБВ = 0,8.

 

Коэффициент полезного действия несогласованной с нагрузкой линии передачи

КПД =  ,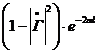

где - модуль коэффициента отражения;

- коэффициент затухания в Нп/м;

- длина линии.

 

Модуль коэффициента отражения

,

где КСВ  = 1/КБВ.

 

 

 

КСВ  = 1/0,8=1,25;

 

Коэффициент затухания

,

, Нп/м.

При расчете КПД величина

находим

 

 

 

 

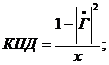
ЗАДАНИЕ 2. ОБЪЕМНЫЕ РЕЗОНАТОРЫ

2.1.Техническое задание

 

1. Нарисовать картину поля заданного типа колебания (см. Приложение 3).

2. Записать выражения для компонент поля соответствующего типа колебаний. В эти выражения надо подставить числовые значения , , 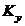, которые заданы типом колебаний и размерами а, b, d, R.

Для прямоугольного резонатора составляющие поля для колебаний типа :

3. Найти резонансную частоту ω_рез резонатора с заданным типом

колебания.

4. Запасенную энергию электромагнитного поля W (считать, что заданное электрическое поле E равно соответственно Е_{z m макс}, E_{y m} макс или Е_{r m макс} – амплитуде поля в том месте, где поле максимально). Для прямоугольного резонатора составляющие поля для колебаний типа :

5. Глубину проникновения в материал стенок.

6. Добротность резонатора Q без учета потерь в диэлектрике.

7. Постоянную времени τ₀. Определить, во сколько раз уменьшится запасенная в резонаторе энергия при свободных колебаниях за время t = 5 с.

 

2.2. Данные для расчета задания 2:

 

Форма – параллелепипед;

Тип колебаний E₁₁₀;

Относительная диэлектрическая проницаемость ε = 1,7;

Проводимость материала стенок γ= 10⁷, 1/Ом∙м;

;

;

Е= 200, В/м;

R=28, см;

d=20, см;

a=20, см;

b=10, см.

 

2.3. Расчёты по п. 1-7 задания №2

 

2.3.1. Нарисовать картину поля заданного типа колебания (см. Приложение 3).

 

2.3.2. Записать выражения для компонент поля соответствующего типа колебаний. В эти выражения надо подставить числовые значения , , 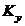, которые заданы типом колебаний и размерами а, b, d, R.

Для прямоугольного резонатора составляющие поля для колебаний типа :

 

;

;

;

;

; ;

,

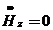где ; ; .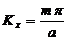

 

, рад/м;

, рад/м;

, рад/м;

, В/м;

, А/м;

, В/м; , В/м; , В/м; , В/м.

 

 

2.3.3. Найти резонансную частоту резонатора с заданным типом колебания.

Резонансные частоты в прямоугольном резонаторе с колебаниями типа

.

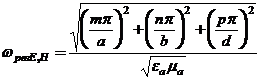, рад/с.

2.3.4. Запасенную энергию электромагнитного поля W (считать, что заданное электрическое поле E равно соответственно , или – амплитуде поля в том месте, где поле максимально).

Запасенная электромагнитная энергия в прямоугольном резонаторе с типом колебания :

;

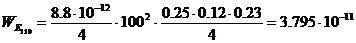Дж.

2.3.5. Глубину проникновения в материал стенок.

.

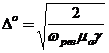, м.

 

2.3.6. Добротность резонатора Q без учета потерь в диэлектрике.

Добротность в прямоугольном резонаторе с колебаниями

,

 

2.3.7. Постоянную времени 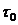. Определить, во сколько раз уменьшится запасенная в резонаторе энергия при свободных колебаниях за время t=5 с.

Энергия при свободных колебаниях тратится на потери и постепенно уменьшается по закону

,

 

где - начальный запас энергии в резонаторе при ;

- постоянная времени.

Собственная частота и резонансная частота связаны друг с другом через добротность так, что

.

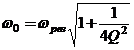Как видно, при больших добротностях в инженерных расчетах этой разницей в величинах резонансной и собственной частоты можно пренебречь и считать .

За время t энергия поля при свободных колебаниях уменьшается .

, с;

 

 

ЗАДАНИЕ 3. КАНАЛЫРАДИОСВЯЗИ

3.1.Техническое задание

1. Для канала ДКМВ определить надежность канала связи.

 

3.2. Данные для расчета задания 3:

 

Длина линии D=200 км;

Мощность передатчика Pвых=400 Вт;

Географическое расположение 40^o с.ш.;

Время связи декабрь 9:00, июнь 12:00;

Коэффициент усиления передающей антенны G_i=4.0;

Фразовая разборчивость J_д=97%;

Надёжность связи pt≥95%.

 

 

3.3. Расчёты по п. 1-11 задания №3 (Канал ДКМВ декабрь 9:00)

 

3.3.1. На основании прогнозов МПЧ (см. приложение 4) выбираем f_р = 3.5 МГц (λ_р = 86 м), для которой отражающим слоем в светлое время суток будет область Е с h_Д = 110 км.

 

3.3.2. Геоцентрический угол, при n=1 и D=200 км:

 

 

3.3.3. Угол падения

 

где a – радиус Земли (a=6370 км)

Для h_д=100 км

 

 

 

 

3.3.4. По графику зависимости Г_Е^’=ψ(λ_р) (см. приложение 4) находим, что Г₀= Г_Е^’=2.7.

 

3.3.5. По ионосферным картам области Е (см. приложение 4) определяем значение f_кр для требуемого месяца года, времени суток и широты. Для декабря 9:00 ч f_кр=2.3 МГц.

 

3.3.6. Действительное значение коэффициента поглощения:

3.3.7. Напряженность электрического поля без учета потерь в ионосфере Е₀:

Воспользовавшись теоремой Пифагора, находим дальность связи r₀ по лучу:

Значение Р_подв определяется произведением Р_вых и коэффициента η полезного действия фидерного тракта, который лежит в пределах η=0.6...0.9. Примем η=0.6.

3.3.8. Медианное значение напряженности поля в точке приема:

 

 

в дБ по отношению к 1 мкВ/м = 42.1 дБ

 

 

3.3.9. Наблюдаемое отношение сигнал/помеха Н на входе приемника в дБ:

для расчетов принимаем Е_П = -40 дБ (по отношению к 1мкВ/м);

 

3.3.10. По графикам зависимости J=Ψ(Н_з) находим, что требуемое защитное отношение Н_з, обеспечивающее J_Д = 97%, составляет 50 дБ (кривая 1).

3.3.11. Определяем

Из графика ΔН=Ψ(p_t) находим надежность связи p_t ≈ 98%, что лучше заданной.

 

 

3.4. Расчёты по п. 1-11 задания №3 (Канал ДКМВ июнь 12:00)

 

3.4.1. На основании прогнозов МПЧ (см. прил. 3, рис. 1) выбираем f_р = 3.5 МГц (λ_р = 86 м), для которой отражающим слоем в светлое время суток будет область Е с h_Д = 110 км.

 

3.4.2. Геоцентрический угол, при n=1 и D=200 км:

 

 

3.4.3. Угол падения

 

где a – радиус Земли (a=6370 км)

 

Для h_д=100 км

 

 

3.4.4. По графику зависимости Г_Е^’=ψ(λ_р) (см. прил. 3, рис.2) находим, что Г₀= Г_Е^’=2.7.

 

3.4.5. По ионосферным картам области Е (см. прил.3, рис. 3) определяем значение f_кр для требуемого месяца года, времени суток и широты. Для декабря 12:00 ч f_кр=3.4 МГц.

 

 

 

3.4.6. Действительное значение коэффициента поглощения:

3.4.7. Напряженность электрического поля без учета потерь в ионосфере Е₀:

Воспользовавшись теоремой Пифагора, находим дальность связи r₀ по лучу:

Значение Р_подв определяется произведением Р_вых и коэффициента η полезного действия фидерного тракта, который лежит в пределах η=0.6...0.9. Примем η=0.6.

3.4.8. Медианное значение напряженности поля в точке приема:

 

 

в дБ по отношению к 1 мкВ/м = 34.2 дБ

 

3.4.9. Наблюдаемое отношение сигнал/помеха Н на входе приемника в дБ:

для расчетов принимаем Е_П = -40 дБ (по отношению к 1мкВ/м);

 

3.4.10. По графикам зависимости J=Ψ(Н_з) находим, что требуемое защитное отношение Н_з, обеспечивающее J_Д = 97%, составляет 50 дБ (кривая 1).

 

3.4.11. Определяем

Из графика ΔН=Ψ(p_t) находим надежность связи p_t ≈ 97%, что лучше заданной.

 

 

СПИСОК ЛИТЕРАТУРЫ

 

1. Яманов Д.Н. Основы электродинамики и распространение радиоволн: Тексты лекций. Часть 1.”Основы электродинамики”.- М.: МГТУ ГА, 2002.-80с.

2. Яманов Д.Н. Электродинамика и техника сверхвысоких частот: Тексты лекций. Часть 2.-М.: МГТУ ГА, 2005.

3. Яманов Д.Н. Основы электродинамики и распространение радиоволн: Тексты лекций. Часть 3. ”Распространение радиоволн”.- М.: МГТУ ГА, 2006.

 

 

 

Приложение 2

Технические данные прямоугольных и круглых волноводов (стандарт, принятый Международной электротехнической комиссией (МЭК))

Пря­мо­уголь­ные вол­новоды
Обозна­чение ти­па волновода	Диа­па­зон час­тот для ос­нов­но­го ти­па вол­ны, ГГц	Внутренние размеры
от	до	ши­ри­на а, мм	вы­со­та b, мм
R26 R32 R40 R48 R70 R84 R100 R120 R140 R180	2,17 2,60 3,22 3,94 5,38 6,57 8,2 9,84 11,9 14,5	3,30 3,95 4,90 5,99 8,17 9,99 12,5 15,0 18,0 22,0	86,3 72,14 58,17 47,55 34,85 28,5 22,86 19,05 15,0 12,954	43,18 34,04 29,08 22,149 15,8 12,62 10,16 9,52 7,9 6,477

 

 

Приложение 3

Картина поля колебания E₁₁₀

...

Приложение 4

Приложение 4

...

 

...