При изучении кинематики КШМ предполагают, что коленчатый вал двигателя вращается с постоянной угловой скоростью ω = const, отсутствуют зазоры в сопряженных деталях, и механизм рассматривают с одной степенью свободы.
Независимой переменной принимают угол поворота кривошипа коленчатого вала φ. При кинематическом анализе устанавливают законы движения звеньев КШМ, и в первую очередь поршня и шатуна. За исходное принимают положение поршня в верхней мертвой точке (точка В1) (рис. 1.20), а направление вращения коленчатого вала по часовой стрелке. При этом для выявления законов движения и аналитических зависимостей устанавливают наиболее характерные точки. Для центрального механизма такими точками являются ось поршневого пальца (точка В), совершающая вместе с поршнем возвратно-поступательное движение вдоль оси цилиндра, и ось шатунной шейки кривошипа (точка А), вращающаяся вокруг оси коленчатого вала О.
Для определения зависимостей кинематики КШМ введем следующие обозначения:
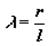l – длина шатуна;
r – радиус кривошипа;
λ – отношение радиуса кривошипа к длине шатуна.
Для современных автомобильных и тракторных двигателей величина λ = 0.25 – 0.31. Для высокооборотных двигателей с целью уменьшения сил инерции возвратно-поступательно движущихся масс применяют более длинные шатуны, чем для малооборотных.
β – угол между осями шатуна и цилиндра, величина которого определяется по следующей зависимости:
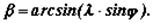
Наибольшие углы β для современных автомобильных и тракторных двигателей составляют 12–18°.
Перемещение (путь) поршня будет зависеть от угла поворота коленчатого вала и определяться отрезком Х (см. рис. 1.20), который равен:
|
|
.
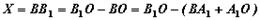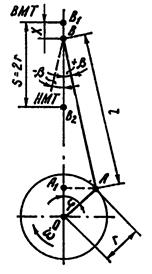
Рис. 1.20. Схема центрального КШМ
Из треугольников А1 АВ и ОА1А следует, что
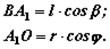
Учитывая, что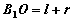 
, получаем:
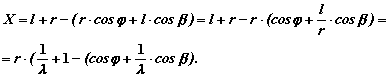
Из прямоугольных треугольников А1АВ и А1ОА устанавливаем, что:
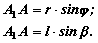
Откуда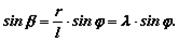 
Так как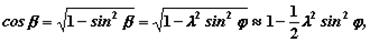 
то, подставив полученные выражения в формулу для перемещения поршня, получим:
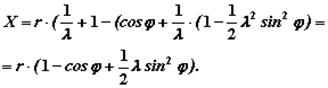
Так как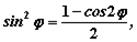 
то 
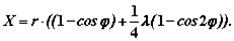
Полученное уравнение характеризует движение деталей КШМ в зависимости от угла поворота коленчатого вала и показывает, что путь поршня можно условно представить состоящим из двух гармонических перемещений: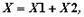 
где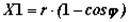 
– путь поршня первого порядка, который имел бы место при наличии шатуна бесконечной длины;
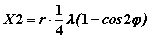– путь поршня второго порядка, т. е. дополнительное перемещение, зависящее от конечной длины шатуна.
На рис. 1.21 даны кривые пути поршня по углу поворота коленчатого вала. Из рисунка видно, что при повороте коленчатого вала на угол, равный 90°, поршень проходит больше половины своего хода.
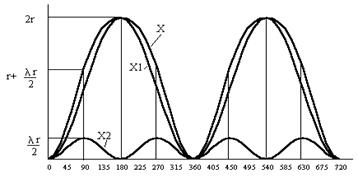
Рис. 1.21. Изменение пути поршня в зависимости от угла поворота коленчатого вала
Скорость поршня определяется как первая производная пути поршня по времени:
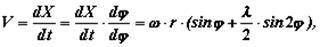
где 
–угловая скорость вращения вала.
Скорость поршня можно представить в виде суммы двух слагаемых:
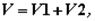
где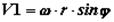 
– гармонически изменяющаяся скорость поршня первого порядка, т. е. скорость, с которой двигался бы поршень при наличии шатуна бесконечно большой длины;
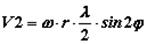– гармонически изменяющаяся скорость поршня второго порядка, т. е. скорость дополнительного перемещения, возникающая вследствие наличия шатуна конечной длины.
На рис. 1.22 даны кривые скорости поршня по углу поворота коленчатого вала. Значения углов поворота коленчатого вала, где поршень достигает максимальных значений скорости, зависят от λ и ее увеличением смещаются в стороны мертвых точек.
|
|
Для практических оценок параметров двигателя используется понятие средней скорости поршня:
.
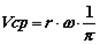Для современных автомобильных двигателей Vср = 8–15 м/с, для тракторных – Vср = 5–9 м/с.
Ускорение поршня определяется как первая производная скорости поршня по времени:
.
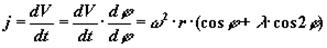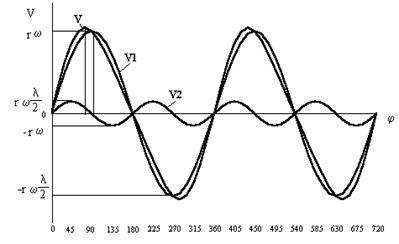
Рис. 1.22. Изменение скорости поршня в зависимости от угла поворота коленчатого вала
Ускорение поршня можно представить в виде суммы двух слагаемых:
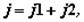
где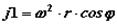 
– гармонически изменяющееся ускорение поршня первого порядка;
– гармонически изменяющееся ускорение поршня второго порядка.
На рис. 1.23 даны кривые ускорения поршня по углу поворота коленчатого вала. Анализ показывает, что максимальное значение ускорения имеет место при нахождении поршня в ВМТ. При положении поршня в НМТ величина ускорения достигает минимального (наибольшего отрицательного) противоположного по знаку значения и абсолютная величина его зависит от φ.
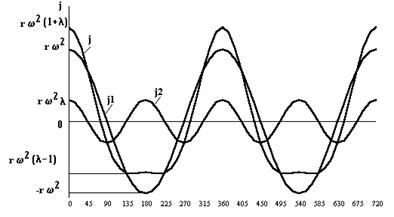
Рис 1.23. Изменение ускорения поршня в зависимости от угла поворота коленчатого вала