Если функция y аргумента x задается при помощи параметрических соотношений
x = x (t), y = y (t) (6.27)
причем x (t) и y (t) – дифференцируемые функции t и x (t)¹0. Производная от y по x находится путем дифференцирования равенств (1):
dx=x/(t)dt, dy=y/(t)dt,
откуда 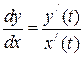 . (6.28)
. (6.28)
Вторую производную от y по x находим, дифференцируя по x соотношение (6.28):
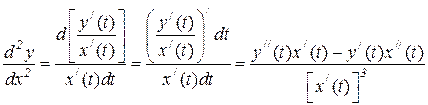 .
.
Пример 6.8 Найти 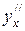 , если x =ln t, y =sin 2 t.
, если x =ln t, y =sin 2 t.
Решение. Дифференцируем исходные соотношения:
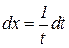 ,
, 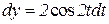 .
.
Отсюда 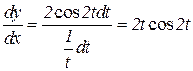 .
.
Найдем вторую производную
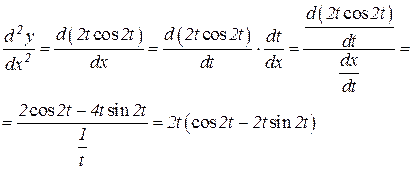 .
.
Дифференциал функции
Пусть функция y = f (x) дифференцируема на отрезке [ a,b ]. Производная этой функции в некоторой точке x отрезка [ a,b ] определяется равенством
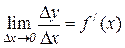 .
.
Отношение 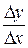 при D x ® 0 стремится к определенному числу f / (x) и, следовательно, отличается от производной f / (x) на величину бесконечно малую:
при D x ® 0 стремится к определенному числу f / (x) и, следовательно, отличается от производной f / (x) на величину бесконечно малую: 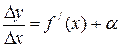 , где a®0 при D x ® 0,
, где a®0 при D x ® 0,
или D y = f / (x)D x + a D x.
Таким образом, приращение функции D y представляет собой сумму двух слагаемых f / (x)D x и a D x, которые являются бесконечно малыми при D x ® 0. Первое слагаемое есть бесконечно малая функция первого порядка относительно D x, так как
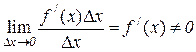 .
.
Произведение a D x есть бесконечно малая величина высшего порядка относительно D x, так как
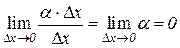 .
.
Первое слагаемое f / (x)D x называется главной частью приращения функции D y.
Дифференциалом функции y = f (x) в точке называется главная часть ее приращения, равная произведению производной f / (x) на приращение D x и обозначается через dy:
dy = f / (x) D x.
Дифференциалом аргумента называется приращение аргумента
dx = D x.
Тогда дифференциал функции равен произведению ее производной на дифференциал аргумента dy = f /(x) dx.
Геометрически дифференциал представляет собой приращение ординаты касательной к графику функции в точке M (x, y).
Основные свойства дифференциала.
6.29 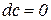 6.30
6.30 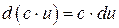 6.31
6.31 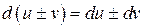
| 6.32 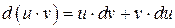 6.33
6.33 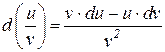 6.34
6.34 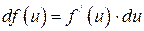
|
Дифференциал dy = f /(x) dx называется дифференциалом первого порядка.
Дифференциал d(dy) от дифференциала dy называется дифференциалом второго порядка функции f (x) и обозначается
d 2 y, то есть d 2y= f //(x)(dx)2 и т.д.
Дифференциал d(d n-1y) от дифференциала d n- 1 y называется дифференциалом n–го порядка функции f (x) и обозначается
d n y, то есть d ny= f (n)(x)(dx)n.
Из определения производной и дифференциала вытекает, что D y = dy+e( D x), где e®0, когда D x ® 0, то есть дифференциал функции отличается от приращения на бесконечно малую высшего порядка, чем D x = dx.
При малых D x справедлива приближенная формула
f (x +D x)– f (x) » f /(x)D x или
f (x +D x) » f /(x)D x + f (x) (6.29)
Пример 9. Найти дифференциал функции 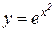 .
.
Решение. Так как dy = f /(x) dx, то 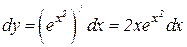 .
.
Пример 10. Найти дифференциал функции y =sinln x.
Решение. 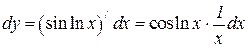 .
.
Пример 11. Найти дифференциал третьего порядка функции y = x 5– 3x3+2.
Решение. Последовательно дифференцируя, получим
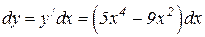
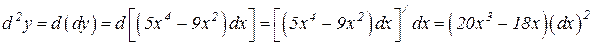
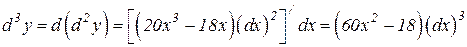 .
.
Пример 12. Вычислить приближенное значение функции y = arcsin x при x = 0,51.
Решение. Рассмотрим функцию y =arcsin x. Полагая x = 0,5, D x = 0,01 и применяя формулу (6.29),
arcsin(x +D x) » arcsin x +(arcsin x)/D x, получаем
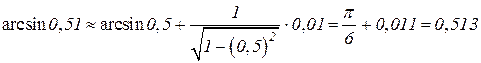 .
.
Пример 13. Вычислить приближенное значение функции y = ln x при x = 2,001.
Решение. Рассмотрим функцию y = ln x. Полагая x = 2, D x = 0,001 и применяя формулу (6.29), 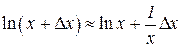 , получаем
, получаем
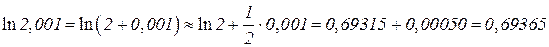 .
.
 Задание 6.1. В задачах 1 - 30 вычислить производную y = f (x).
Задание 6.1. В задачах 1 - 30 вычислить производную y = f (x).
| 1. | 1. 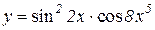 2.
2. 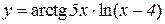 3.
3. 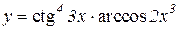 4.
4. 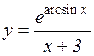 5.
5. 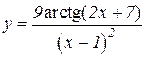
| 2. | 1. 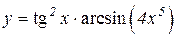 2.
2. 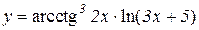 3.
3. 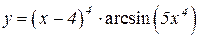 4.
4. 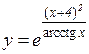 5.
5. 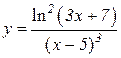
|
| 3. | 1. 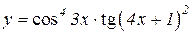 2.
2. 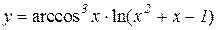 3.
3. 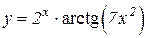 4.
4. 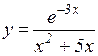 5.
5. 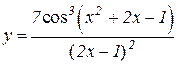
| 4. | 1. 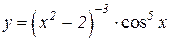 2.
2. 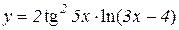 3.
3. 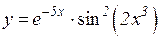 4.
4. 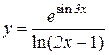 5.
5. 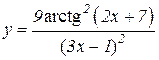
|
| 5. | 1. 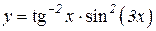 2.
2. 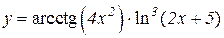 3.
3. 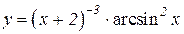 4.
4. 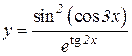 5.
5. 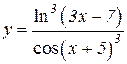
| 6. | 1. 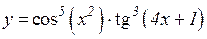 2.
2. 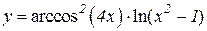 3.
3. 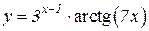 4.
4. 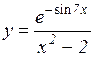 5.
5. 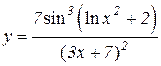
|
| 7. | 1. 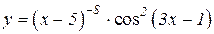 2.
2. 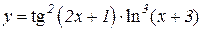 3.
3. 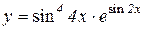 4.
4. 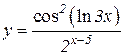 5.
5. 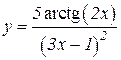
| 8. | 1. 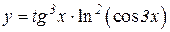 2.
2. 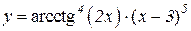 3.
3. 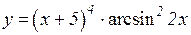 4.
4. 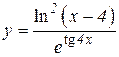 5.
5. 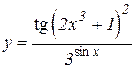
|
| 9. | 1. 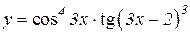 2.
2. 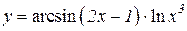 3.
3. 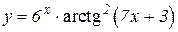 4.
4. 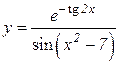 5.
5. 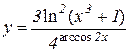
| 10. | 1. 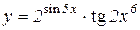 2.
2. 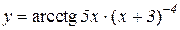 3.
3. 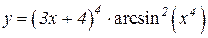 4.
4. 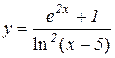 5.
5. 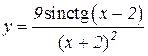
|
| 11. | 1. 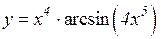 2.
2. 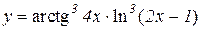 3.
3. 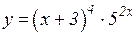 4.
4. 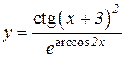 5.
5. 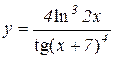
| 12. | 1. 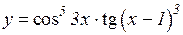 2.
2. 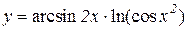 3.
3. 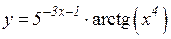 4.
4. 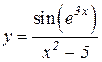 5.
5. 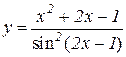
|
| 13. | 1. 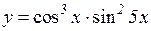 2.
2. 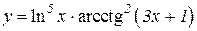 3.
3. 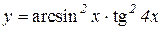 4.
4. 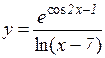 5.
5. 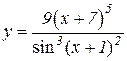
| 14. | 1. 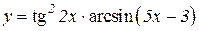 2.
2.  3.
3. 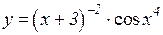 4.
4. 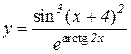 5.
5. 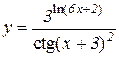
|
| 15. | 1. 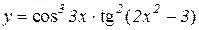 2.
2. 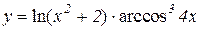 3.
3. 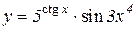 4.
4. 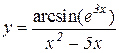 5.
5. 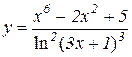
| 16. | 1. 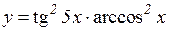 2.
2. 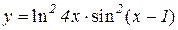 3.
3. 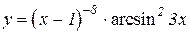 4.
4. 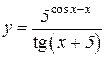 5.
5. 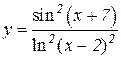
|
| 17. | 1. 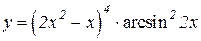  2.
2. 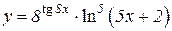 3.
3. 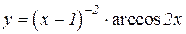 4.
4. 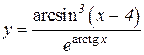 5.
5. 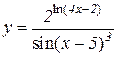
| 18. | 1. 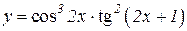  2.
2. 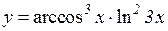 3.
3. 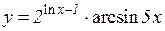 4.
4. 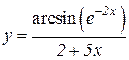 5.
5. 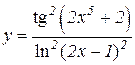
|
| 19. | 1. 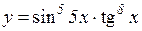  2.
2. 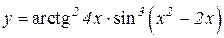 3.
3. 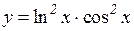 4.
4. 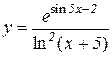 5.
5. 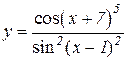
| 20. | 1. 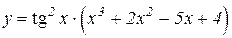 2.
2. 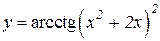 3.
3. 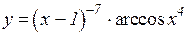 4.
4. 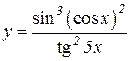 5.
5. 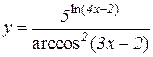
|
| 21. | 1. 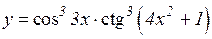  2.
2. 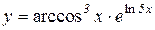 3.
3. 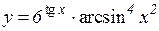 4.
4. 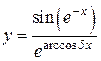 5.
5. 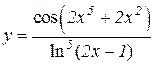
| 22. | 1. 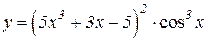 2.
2. 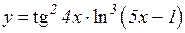 3.
3. 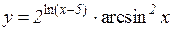 4.
4. 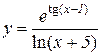 5.
5. 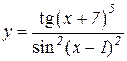
|
| 23. | 1. 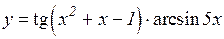  2.
2. 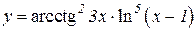 3.
3. 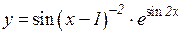 4.
4. 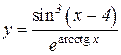 5.
5. 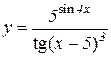
| 24. | 1. 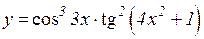  2.
2. 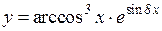 3.
3. 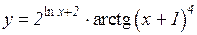 4.
4. 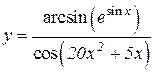 5.
5. 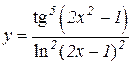
|
| 25. | 1. 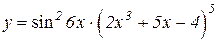 2.
2. 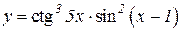 3.
3. 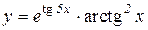 4.
4. 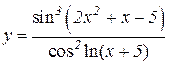 5.
5. 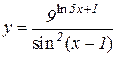
| 26. | 1. 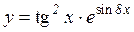  2.
2. 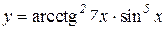 3.
3. 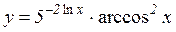 4.
4. 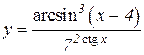 5.
5. 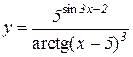
|
| 27. | 1. 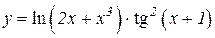  2.
2. 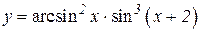 3.
3. 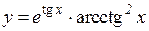 4.
4. 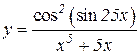 5.
5. 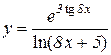
| 28. | 1. 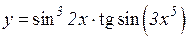  2.
2. 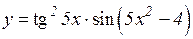 3.
3. 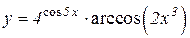 4.
4. 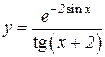 5.
5. 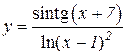
|
| 29. | 1. 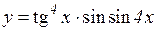 2.
2. 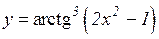 3.
3. 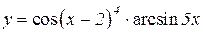 4.
4. 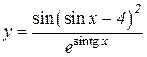 5.
5. 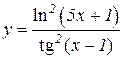
| 30. | 1. 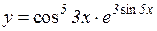  2.
2. 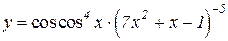 3.
3. 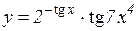 4.
4. 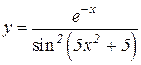 5.
5. 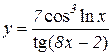
|
Задание 6.2. Продифференцировать данные функции, применяя метод логарифмического дифференцирования.
| 1. | a) 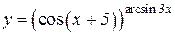 b)
b) 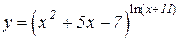
| 2. | a) 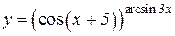 b)
b) 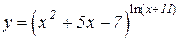
| |
| 3. | a) 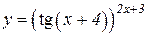 b)
b) 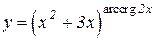
| 4. | a) 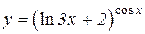 b)
b) 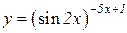
| |
| 5. | a) 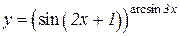 b)
b) 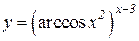
| 6. | a) 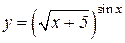 b)
b) 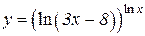
| |
| 7. | a) 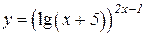 b)
b) 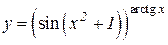
| 8. | a) 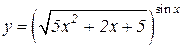 b)
b) 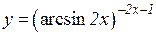
| |
| 9. | a) 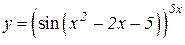 b)
b) 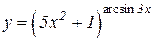
| a) 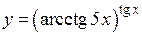 b)
b) 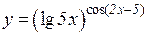
| ||
a) 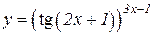 b)
b) 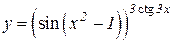
| a) 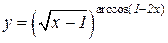 b)
b) 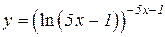
| |||
a) 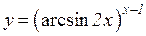 b)
b) 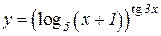
| a) 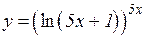 b)
b) 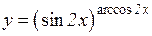
| |||
a) 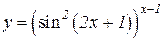 b)
b) 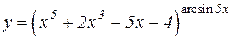
| a) 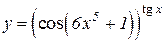 b)
b) 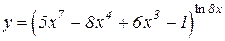
| |||
a) 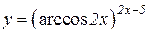 b)
b) 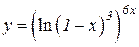
| 18. | a) 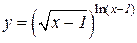 b)
b) 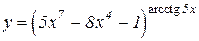
| ||
a) 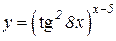 b)
b) 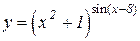
| 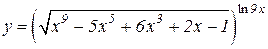 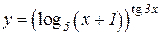
| |||
a) 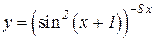 b)
b) 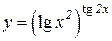
| a) 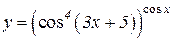 b)
b) 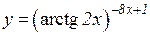
| |||
a) 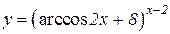 b)
b) 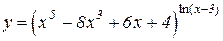
| a) 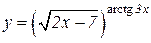 b)
b) 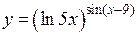
| |||
a) 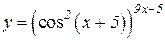 b)
b) 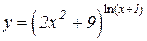
| a) 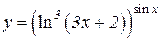 b)
b) 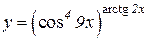
| |||
a) 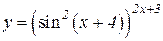 b)
b) 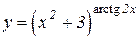
| a) 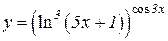 b)
b) 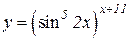
| |||
a) 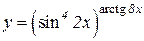 b)
b) 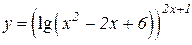
| a) 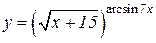 b)
b) 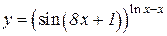
| |||
Задание 6.3. Найти первую и вторую производные функций.
| 1. | a) 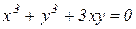 b)
b) 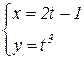
| 2. | a) 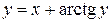 b)
b) 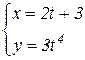
|
| 3. | a) 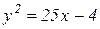 b)
b) 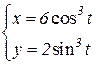
| 4. | a) 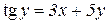 b)
b) 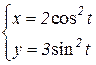
|
| 5. | a) 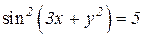 b)
b) 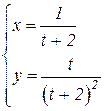
| 6. | a) 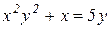 b)
b) 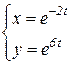
|
| 7. | a) 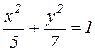 b)
b) 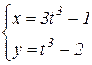
| 8. | a) 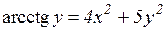 b)
b) 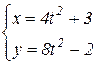
|
| 9. | a) 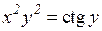 b)
b) 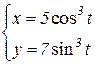
| 10. | a) 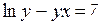 b)
b) 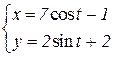
|
| 11. | a) 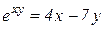 b)
b) 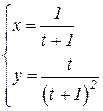
| 12. | a) 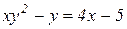 b)
b) 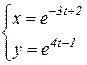
|
| 13. | a) 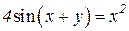 b)
b) 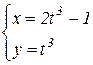
| 14. | a) 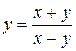 b)
b) 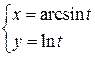
|
| 15. | a) 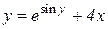 b)
b) 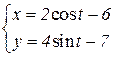
| 16. | a) 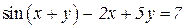 b)
b) 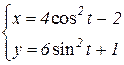
|
| 17. | a) 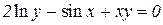 b)
b) 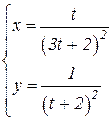
| 18. | a) 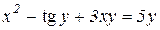 b)
b) 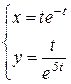
|
| 19. | a) 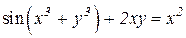 b)
b) 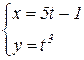
| 20. | a) 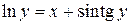 b)
b) 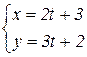
|
| 21. | a) 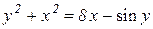 b)
b) 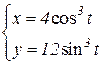
| 22. | a) 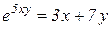 b)
b) 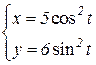
|
| 23. | a) 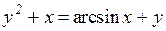 b)
b) 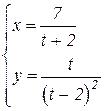
| 24. | a) 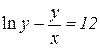 b)
b) 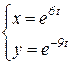
|
| 25. | a) 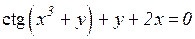 b)
b) 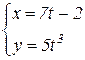
| 26. | a) 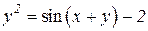 b)
b) 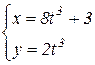
|
| 27. | a) 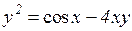 b)
b) 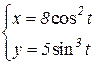
| 28. | a) 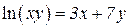 b)
b) 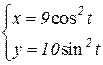
|
| 29. | a) 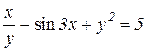 b)
b) 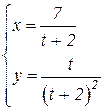
| 30. | a) 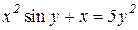 b)
b) 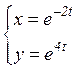
|
Задание 6.4. Вычислить с помощью дифференциала приближенное значение функции в заданной точке.
| 1. | 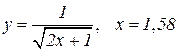
| 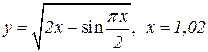
| |
| 3. | 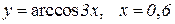
| 4. | 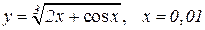
|
| 5. | 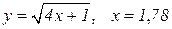
| 6. | 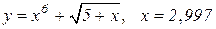
|
| 7. | 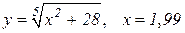
| 8. | 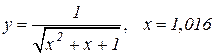
|
| 9. | 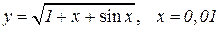
| 10. | 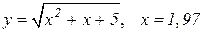
|
| 11. | 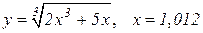
| 12. | 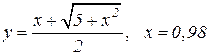
|
| 13. | 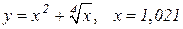
| 14. | 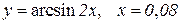
|
| 15. | 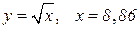
| 16. | 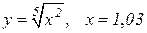
|
| 17. | 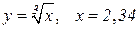
| 18. | 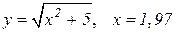
|
| 19. | 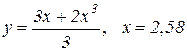
| 20. | 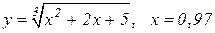
|
| 21. | 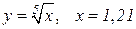
| 22. | 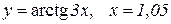
|
| 23. | 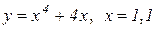
| 24. | 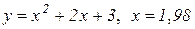
|
| 25. | 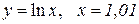
| 26. | 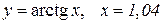
|
| 27. | 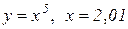
| 28. | 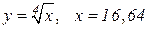
|
| 29. | 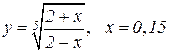
| 30. | 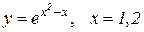
|