Производная функции
Дифференцирование функций, заданных явно
Производной функции y = f (x) в точке x 0 называется предел отношения приращения функции в этой точке к приращению аргумента, когда последнее стремится к нулю. Производная функции y = f (x) обозначается через y /, или f / (x).
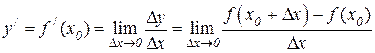
Операция нахождения производной f / (x) от функции f (x) называется дифференцированием этой функции.
Геометрически значение производной функции y = f (x) в точке x = x 0 равно тангенсу угла, образованного положительным направлением оси Ох и касательной, проведенной к графику функции в точке с абсциссой x 0, то есть f /(x 0)=tg a (рис 6.1).
| Число tg a называют угловым коэффициентом касательной и обозначают k, то есть k = f /(x 0)=tg a. В прямоугольной системе координат уравнения касательной и нормали к некоторой кривой y = f (x) в точке М 0(x 0; y 0) имеют вид |  Рис 6.1
Рис 6.1
|
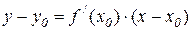 – уравнение касательной,
– уравнение касательной,
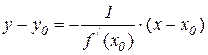 – уравнение нормали.
– уравнение нормали.
Если функция y = f (x) описывает какой–либо физический процесс, то производная y / есть скорость протекания этого процесса. В этом состоит физический смысл производной.
Основные правила дифференцирования.
Пусть даны функции, имеющие производные u = u (x) и v = v (x), c =const
6.1 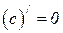 6.2
6.2 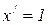 6.3
6.3 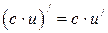
| 6.4 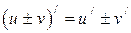 6.5
6.5 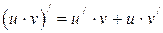
|
6.6 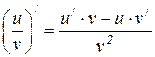
6.7 если дана сложная функция y = f (u), где u = u (x), то есть y = f [ u (x)], где функции f (u) и u (x) имеют производные, то 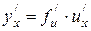 (правило дифференцирования сложной функции).
(правило дифференцирования сложной функции).
Основные формулы дифференцирования.
6.8 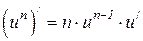 6.9
6.9 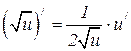 6.10
6.10 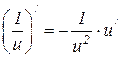 6.11
6.11 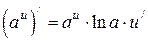 6.12
6.12 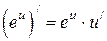 6.13
6.13 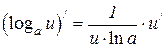 6.14
6.14 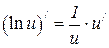 6.15
6.15 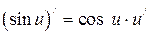 6.16
6.16 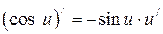 6.17
6.17 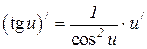
| 6.18 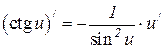 6.19
6.19 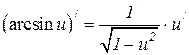 6.20
6.20 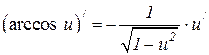 6.21
6.21 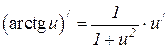 6.22
6.22 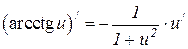 6.23
6.23 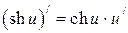 6.24
6.24  6.25
6.25 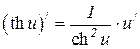 6.26
6.26 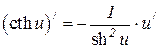
|
Пример 1. Найти производную функции 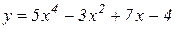 .
.
Решение. Дифференцируем как сумму по формулам 6.4, 6.1, 6.3 правил дифференцирования и применяем формулу 6.8
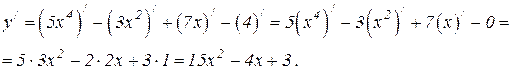
Пример 2. Найти y // функции 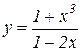 .
.
Решение. Дифференцируем как частное по формуле 6.5 правил дифференцирования и применяем формулы 6.2, 6.1 и 6.8
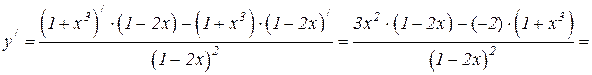
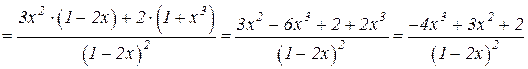 .
.

Пример 3. Найти y / функции 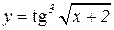 .
.
Решение. Дифференцируем, применяя формулы производной сложной функции и формулы 6.8 и 6.12
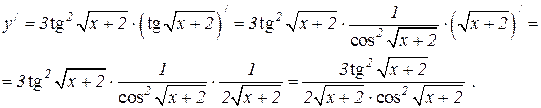
Пример 4. Найти y / функции 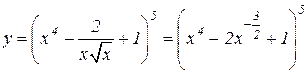 .
.
Решение. Вводим сначала дробные и отрицательные показатели, затем дифференцируем, применяя формулы 6.3, 6.2 и 6.1 и формулу 6.8
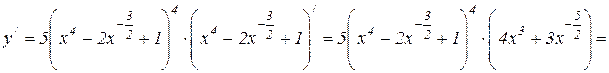
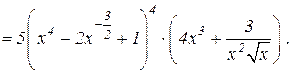
Пример 5. Найти y / функции 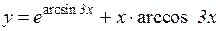 .
.
Решение. Применяем сначала формулу 6.3, а для второго слагаемого формулу 6.4. Затем используем формулы 6.9, 6.14, 6.8 и 6.15
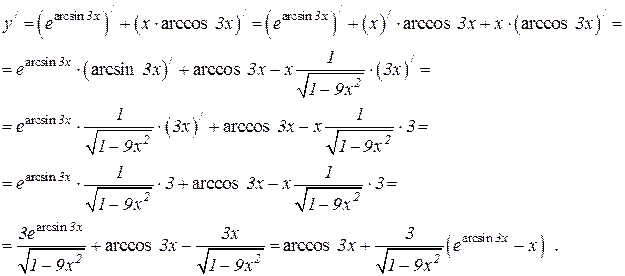
Логарифмический метод.
Иногда, прежде чем находить производную от заданного выражения, лучше выражение преобразовать так, чтобы процесс дифференцирования упрощался. Во многих случаях оказывается выгодным, прежде чем дифференцировать заданную функцию, взять ее логарифм, определить затем производную от этого логарифма и по производной от логарифма отыскать производную от заданной функции. Такой прием называется способом логарифмического дифференцирования.
Метод логарифмического дифференцирования позволяет находить производные от сложной функции вида 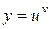 , где u, v - функции аргумента x. Действительно, логарифмируя обе части исходного равенства, получаем
, где u, v - функции аргумента x. Действительно, логарифмируя обе части исходного равенства, получаем
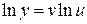 .
.
Дифференцируя последнее равенство, имеем
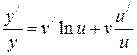 .
.
Умножая обе части равенства на y и заменяя затем y через uv, окончательно получаем
 .
.
Пример 6. Найти y /, если 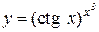 .
.
Решение. Здесь основание и показатель степени зависят от x. Логарифмируя, получим
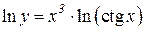 (так как
(так как 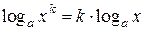 ).
).
Продифференцируем обе части последнего равенства по x. Так как y является функцией от x, то ln y есть сложная функция x и 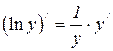 . Следовательно,
. Следовательно,
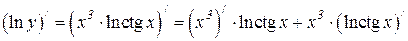
или 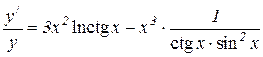 .
.
Умножив последнее равенство на y, получим
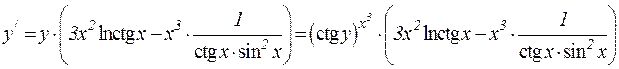 .
.
Дифференцирование функций, заданных неявно
Если y как функция от x задается посредством соотношения F (x, y)=0, где F (x, y) – выражение, содержащее x и y, то y называется неявной функцией от x. В некоторых случаях уравнение F (x, y)=0 удается разрешить относительно y, и тогда можно перейти от неявного способа задания функции к явному y = f (x), в других случаях такой переход невозможно осуществить. Независимо от возможности перехода производная от y по x для функции, заданной неявно, может быть определена следующим образом:
1. Находим производную от левой части равенства F (x, y)=0, учитывая при этом y как функцию от x, и приравниваем ее к нулю.
2. Разрешаем полученное уравнение относительно y /; в результате будем иметь выражение производной от неявной функции в виде y /= f (x, y). Для определения второй производной от функции, заданной неявно, дифференцируем равенство y /= f (x, y) (рассматривая y как функцию от x), а затем в правой части заменяем y / его выражением из равенства y /= f (x, y). Аналогично поступаем при нахождении производных более высоких порядков.
Пример 7. Найти y //, если arctg y – y + x = 0.
Решение. Дифференцируем данное выражение, рассматривая y как функцию от x: 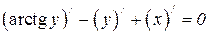
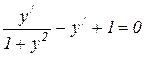 или
или 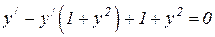 ,
, 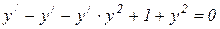 ,
, 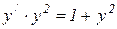 ,
,
откуда 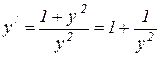 .
.
Находим далее y //: 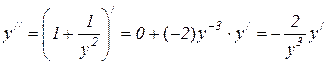 .
.
В последнее равенство вместо y / подставляем его значение. Тогда получаем 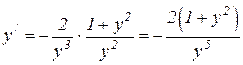 .
.