Важным этапом прогнозирования социально-экономических явлений является оценка точности и достоверности прогнозов.
Точность прогноза тем выше, чем меньше величина ошибки, которая представляет собой разность между прогнозируемым и фактическим значением исследуемой величины.
Вся проблема состоит в том, чтобы вычислить ошибку прогноза, так как фактическое значение прогнозируемой величины станет известно только в будущем. Следовательно, методы оценки точности по уже свершившимся событиям (апостериорные) не имеют практической ценности, так как являются лишь констатацией факта. При разработке прогноза оценку его точности требуется производить заранее (априорно), когда истинное значение прогнозируемой величины еще не известно.
Все показатели оценки точности статистических прогнозов условно можно разделить на три группы:
·Аналитические (абсолютные и относительные);
·сравнительные;
Аналитические показатели т очности прогноза позволяют количественно определить величину ошибки прогноза. К ним относятся следующие показатели точности прогноза:
1) Абсолютная ошибка прогноза (Sабс) определяется как разность между эмпирическим и прогнозным значениями признака и вычисляется по формуле:
где уtфакт – фактическое значение признака;
уtпогн - прогнозное значение признака.
2) Относительная ошибка прогноза (Sотн) может быть определена как отношение абсолютной ошибки прогноза
к фактическому значению признака (уt):
3) Средним показателем точности прогноза является средняя абсолютная ошибка прогноза (
), которая определяется как средняя арифметическая простая из абсолютных ошибок прогноза по формуле вида:
|
|
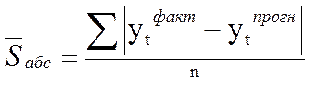
де n – длина временного ряда.
Средняя абсолютная ошибка прогноза показывает обобщенную характеристику степени отклонения фактических и прогнозных значений признака и имеет ту же размерность, что и размерность изучаемого признака.
4) средняя относительная ошибка прогноза:
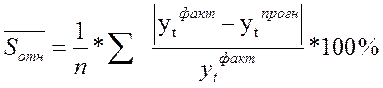
5) Для оценки точности прогноза используется средняя квадратическая абсолютная ошибка прогноза, определяемая по формуле:
В качестве сравнительного показателя точности прогноза используется коэффициент корреляции между прогнозными и фактическими значениями признака, который определяется по формуле:
6) 
Используя данный коэффициент в оценке точности прогноза следует помнить, что коэффициент парной корреляции в силу своей сущности отражает линейное соотношение коррелируемых величин и характеризует лишь взаимосвязь между временным рядом фактических значений и рядом прогнозных значений признаков. И даже если коэффициент корреляции R = 1, то это еще не предполагает полного совпадения фактических и прогнозных оценок, а свидетельствует лишь о наличии линейной зависимости между временными рядами прогнозных и фактических значений признака.
Одним из показателей оценки точности статистических прогнозов является коэффициент несоответствия (КН), который был предложен Г. Тейлом и может рассчитываться:
7) 
КН = 0, если имеет место полное совпадение фактических и прогнозных значений признака.
|
|
Пример 1.
Таблица 1
Сравнительная оценка фактических и прогнозных значений потребления кондитерских изделий в год
| Год | Фактическое значение потребления конд. изделий в год (кг/чел) | Прогнозное значение потребления конд. изделий в год (кг/чел) | Оценка точности | |||
| Sабс | Sотн, % | (уфакт-упрогн)2 | 
| |||
| 15,9 | 16,3 | -0,4 | -2,52 | 0,16 | 6,25 | |
| 17,2 | 17,3 | -0,1 | -0,58 | 0,01 | 1,44 | |
| 18,1 | 18,2 | -0,1 | -0,55 | 0,01 | 0,09 | |
| 19,8 | 19,2 | 0,6 | 3,03 | 0,36 | 1,96 | |
| 21,2 | 20,0 | 1,2 | 5,66 | 1,44 | 7,84 | |
| среднее |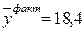 
| 
| ||||
| ошибка | 
| 
| 
| КН.=0,336 |
Решение
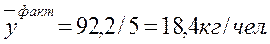
Расчет коэффициента корреляции:
|
| 
| 
| *
|
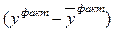
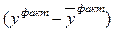| -2,5 | 6,25 | -2,1 | 4,41 | 5,25 |
| -1,2 | 1,44 | -1,1 | 1,21 | 1,32 |
| -0,3 | 0,09 | -0,2 | 0,04 | 0,06 |
| 1,4 | 1,96 | 0,8 | 0,64 | 1,12 |
| 2,8 | 7,84 | 1,6 | 2,56 | 4,4 |
| Сумма | 17,58 | - | 8,86 | 12,15 |
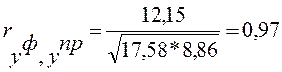
Линейный коэффициент корреляции изменяется в пределах от -1 до 1: [ 
].
| Коэффициент корреляции | Интерпретация точности |
| >0,7 | Высокая |
| 0,5-0,7 | Хорошая |
| 0,3-0,5 | Удовлетворительная |
| < 0,3 | Неудовлетворительная |
При этом точность прогноза оценивается величиной доверительного интервала для заданной вероятности его осуществления, а под достоверностью понимают оценку вероятности осуществления прогноза в заданном доверительном интервале. Таким образом, точность прогноза выражается с помощью вероятностных пределов фактической величины от прогнозируемого значения.
Следует отметить, что точное совпадение фактических данных и прогностических точечных оценок, полученных путем экстраполяции кривых, характеризующих тенденцию, явление маловероятное. И этому виной следующие источники погрешностей:
|
|
1) выбор формы кривой (порядка полинома и т. д.), характеризующей тренд, содержит элемент субъективизма. Во всяком случае, часто нет твердой основы для того чтобы утверждать, что выбранная форма кривой является единственно возможной или тем более наилучшей для экстраполяции в данных конкретных условиях;
2) оценивание параметров кривых (иначе говоря, оценивание тренда) производится на основе ограниченной совокупности наблюдений, каждое из которых содержит случайную компоненту. В силу этого параметрам кривой, а следовательно, и ее положению в пространстве свойственна некоторая неопределенность;
3) тренд характеризует некоторый средний уровень ряда на каждый момент времени. Отдельные наблюдения, как правило, отклонялись от него в прошлом. Естественно ожидать, что подобного рода отклонения будут происходить и в будущем.
Погрешность, связанная со вторым и третьим ее источниками, и может быть отражена в виде доверительного интервала прогноза при принятии некоторых допущений о свойстве ряда. При расчете прогноза необходимо вводить поправку на недостаточный объем выборки. С этой целью в формулу вычисления границ доверительного интервала необходимо ввести коэффициент — значение t - статистики Стьюдента (коэффициент kα):
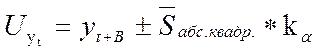
- средняя квадратическая ошибка прогноза.
В – период упреждения.
В нашем Примере 1: Доверительный интервал прогноза для следующего 6 года равен:
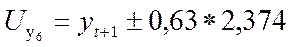
Доверительный интервал записывается в виде «вилки» - мак и мин величины:
[min – max]
Рис. 1 Доверительный интервал прогноза
Таблица 2
Значения kα для оценки доверительных интервалов прогноза относительно линейного тренда
| Число уровней в ряде (n) | Период упреждения В | |||||
| 2,374 | 2,741 | 3,151 | 3,589 | 4,046 | - | |
| 2,094 | 2,337 | 2,608 | 2,901 | 3,208 | 3,528 | |
| 1,932 | 2,106 | 2,300 | 2,510 | 2,733 | 2,965 | |
| 1,826 | 1,956 | 2,102 | 2,260 | 2,429 | 2,605 | |
| 1,749 | 1,851 | 1,965 | 2,088 | 2,220 | 2,358 | |
| 1,692 | 1,774 | 1,865 | 1,964 | 2,069 | 2,180 | |
| 1,647 | 1,714 | 1,788 | 1,869 | 1,956 | 2,047 | |
| 1,611 | 1,667 | 1,729 | 1,796 | 1,868 | 1,944 | |
| 1,581 | 1,629 | 1,682 | 1,738 | 1,799 | 1,863 | |
| 1,557 | 1,528 | 1,643 | 1,691 | 1,743 | 1,798 | |
| 1,536 | 1,572 | 1,611 | 1,653 | 1,697 | 1,745 |