Электрическая цепь II порядка содержит два противоположных реактивных элемента – L и C. При последовательном соединении элементов L и C электрическую цепь называют последовательным колебательным контуром, а при параллельном соединении элементов L и C – параллельным колебательным контуром. Характер переходного процесса в электрической цепи II порядка зависит от добротности контура, определяемой формулой: Q=ρ/rпот,
где ρ – характеристическое сопротивление контура, rпот – сопротивление потерь. Для последовательного контура rпот = r, а для параллельного контура rпот = r + rвн, где rвн – сопротивление, вносимое в контур внешними цепями.
При добротности Q<0,5 переходный процесс в электрической цепи II порядка носит апериодический характер, при Q>0,5 – колебательный. В случае если активное сопротивление контура r равно нулю, эквивалентная добротность параллельного колебательного контура будет определяться формулой: Qэкв = R/ρ.
В задании №2 необходимо рассчитать переходный процесс, протекающий в электрической цепи с двумя реактивными элементами.
Исходные данные:
· номер группы №гр=926 (abc), номер студента по журналу №ст=12 (km);
· напряжение источника питания Е=10(c+k+1)=80 [B];
· индуктивность L=m+1=3 [мГн];
· емкость C=10 + k - m=9 [мкФ];
· R = ρ/(3+k), ρ = 18,17, R = 4,55 Ом
Порядок расчета
1. Определяется независимая переменная. Для упрощения расчета в качестве независимой переменной в параллельном контуре выбирается ток через индуктивность iL(t).
2. Составляется дифференциальное уравнение для переходного процесса в электрической цепи, и записывается его общее решение
iL(t) = iсв(t) + iпр
3. Определяются начальные условия, по которым рассчитывается постоянные и принужденные составляющие в решении дифференциальных уравнений.
|
|
До коммутации
iL(0) = E/2R = 8,79 мА
Uc(0) = 0
После коммутации
iпр = 0
uпр = 0
Записывается решение дифференциального уравнения для свободной составляющей
iсв(t) = A∙eαt∙sin(ωct + ϴ),
где А и ϴ - постоянные интегрирования в решении дифференциального уравнения, α и ωс - действительная и мнимая части корней характеристического уравнения.
Для составления характеристического уравнения рассчитывается комплексное входное сопротивление электрической цепи, в которой все источники ЭДС заменяются коротким замыканием, а все разомкнутые ветви отбрасываются.
Zвх = Xc + XL + R
Xc = 1/jωC, XL = jωL
1/pC + pL + R = 0
P2 CL + pCR + 1 =0
Д = -10,63∙10-8
P1,2 = -0,76∙103 ± 6∙103i
α = -0,76∙103, ωc = 6∙103
Действительная часть корней характеристического уравнения α определяет постоянную времени затухания колебаний контура
τ = 1/│α│= 1/│-0,76∙103│= 1,32∙10-3 [c],
а мнимая часть корней характеристического уравнения – период этих колебаний
T = 2π/ωC = 6,28/6∙103 = 1,05∙103
4. Определяются постоянные интегрирования А и ϴ
iL(t) = iсв(t) + iпр, iL(t) = A∙e-0,76∙1000∙t sin(6∙103t + ϴ)
UL(t) = L∙(diL/dt)
UL(t) = L(-0,76∙103∙e-0,76∙1000∙t ∙A∙sin(6∙103t + ϴ) + A∙6∙103∙e-0,76∙1000∙t ∙cos(6∙103t + ϴ))
iL(t) = A∙sinϴ
UL(t) = 0
iL(t) = E/2R = 8,79
A∙sinϴ = 8,79
A = 8,79/sinϴ
-2,28∙8,79 + 18∙8,79∙ctgϴ = 0
158,22∙ctgϴ = 20,04
ϴ = 82,59
A = 8,79/sin(82,59) = 8,88
iL(t) = 8,88∙e-0,76∙1000∙t ∙sin(6∙103t + 82,59)
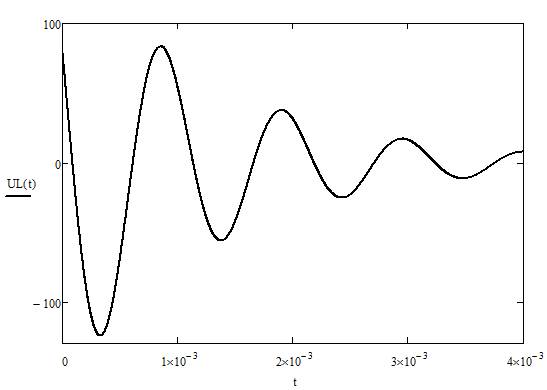
5. Построить временные диаграммы тока через индуктивность и напряжения на емкости на интервале времени от t = 0 до t = 3τ, используя следующие правила:
|
|
· построить затухающую экспоненту x(t) = A∙eαt и симметричную ей относительно оси экспоненту x(t) = -A∙eαt.
· рассчитать период колебаний и отложить на оси времени характерные точки (T/4, T/2, 3T/4 и т.д.);
· используя значения гармонического колебания в характерных точках и экспоненциальную огибающую, построить временные диаграммы изменения токов и напряжений во время переходного процесса.
x(t) = A∙eαt, x(t) = -A∙eαt
x(t) = ±8,88∙e-0,76∙1000∙t
x(0) = 8,88;
x(0,5τ) = 5,39;
x(τ) = 3,24;
x(1,5 τ) = 1,96;
x(2 τ) = 1,19;
x(2,5 τ) = 0,72;
x(3 τ) = 0,44
Задание №3
Расчет формы и спектра сигналов при нелинейных преобразованиях
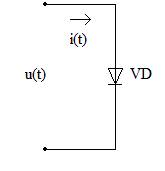
К нелинейному элементу (полупроводниковому диоду) приложено напряжение, имеющее постоянную и переменную составляющие
u(t) = U0 +Um ∙ cos ωt
В расчетном задании используется кусочно-линейная аппроксимация ВАХ нелинейного элемента. При u(t)<U1 (U1 – пороговое напряжение) диод смещен в обратном направлении и не пропускает ток, его сопротивление Rд стремится к бесконечности. При u(t)≥U1 диод смещен в прямом направлении и его ток линейно зависит от приложенного напряжения. Наклон ВАХ нелинейного элемента характеризуется крутизной S = ∆I/∆U [мА/B]. Величина, обратная крутизне, является сопротивлением диода в прямом направлении Rд = 1/S.
Исходные данные
· номер группы №гр=926 (abc), номер студента по журналу №ст=12 (km);
· постоянная составляющая входного сигнала U0 = 0,5 [B], пороговое напряжение нелинейного элемента U1 = 1 [B];
· амплитуда переменной составляющей входного напряжения
|
|
Um = 1 +0,1c = 1,6 [B];
· крутизна ВАХ нелинейного элемента S = c + №ст = 18 [мА/В];
· период колебаний переменной составляющей входного напряжения
T = №ст = 12 [мкс], частота ω = 0,52∙106
Требуется:
1) рассчитать угол отсечки ϴ, в радианах и градусах
cosϴ = (U1 – U0)/Um = (1-0,5)/1,6 = 0,31
2) рассчитать амплитуду тока диода
Im = S∙Um∙(1-cosϴ) = 18∙10-3∙1,6∙0,69 = 19,87 [мА];
3) записать выражение для мгновенного значения тока
i(t) = (Im/(1-cosϴ))∙(cos ωt - cosϴ) = (19,87∙10-3/0,69)∙(cos 0,52∙106 – 0,31) = 0,029∙cos 0,52∙106 – 0,009;
4) вычислить постоянную составляющую тока
I0 = Im∙((sinϴ - cosϴ)/π(1 – cosϴ)) = 19,87∙10-3∙((0,95-1,26∙0,31)/(3,14∙0,69)) = 5,13 [мА];
5) изобразить временные диаграммы напряжения u(t)
6) вычислить амплитуду первой гармоники тока
Im1 = Im∙((ϴ - sinϴ∙cosϴ)/π∙(1-cosϴ)) = 19,87∙10-3∙((1,26-0,95∙0,31)/(3,14∙0,69)) = 8,88 [мА];
7) используя общее выражение для n – ой гармоники тока
Imn = Im∙((2(sinϴ∙cosϴ - n∙cos(n∙ϴ)∙sinϴ)/(π∙n∙(n2 – 1)∙(1-cosϴ)))
Im2 = 19,87∙10-3∙(((2(0,95∙0,31 - 2∙(-0,81)∙0,95))/12,9996)= 5,59 [мА];
Im3 = 19,87∙10-3∙(((2(0,29 - 3∙(-0,8)∙0,95))/51,998) = 1,96 [мА];
Im4 = 19,87∙10-3∙(((2(0,29 - 4∙0,32∙0,95))/129,996) = -0,28 [мА];
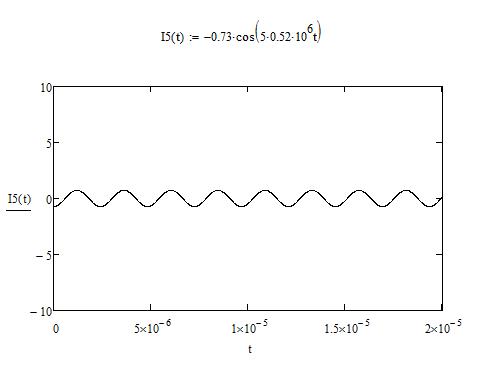
Im5 = 19,87∙10-3∙(((2(0,29 - 5∙0,9999∙0,95))/259,992) = -0,73 [мА];
8) 
По полученным данным построить диаграмму спектра тока нелинейного элемента
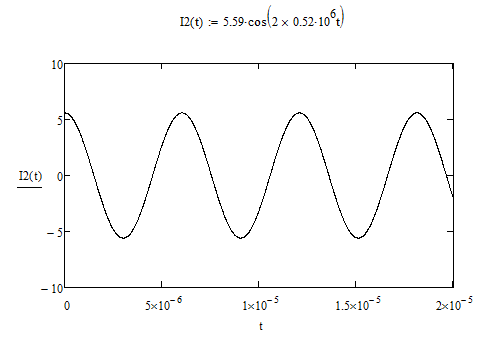
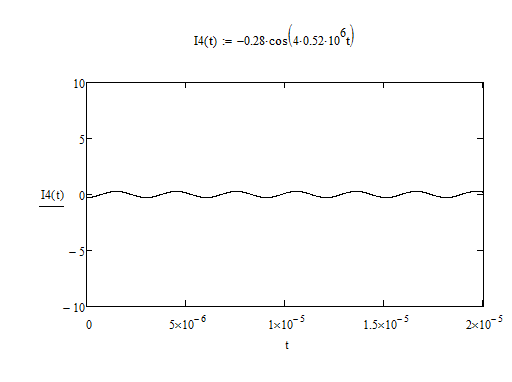
9) Используя вычислительные возможности программы MathCAD, построить временную диаграмму тока для первых пяти гармоник
i(t) = I0 + Im1∙cos ω1t + Im2∙cos 2ω1t + Im3∙cos 3ω1t + Im4∙cos 4ω1t + Im5∙cos 5 ω1t
Ъ
Список литературы
1) В.П. Попов «Основы теории цепей», Москва – «Высшая школа», 1985.
2) Л.А. Бессонов «Теоретические основы электротехники», Москва – «Высшая школа», 1984.
3) Методическое указание к практическим занятиям. «Теоретические основы электротехники».