Теория множеств.
Понятия множества. Способы задания. Примеры.
Множество - это совокупность объектов, называемых элементами множества.
Подмножества. Равенство множеств.
Операции над множествами: объединение, пересечение, дополнение. Определение. Свойства. Примеры.
Объединение
Определение
Пусть даны два множества A и B.
Тогда их объединением называется множество
Примеры
Пусть A = {1,2,3,4}, B = {3,4,5,6,7}. Тогда
· 
· 
Свойства
· Объединение множеств является бинарной операцией на произвольномбулеане 2 X;
· Операция объединения множеств коммутативна: 
· Операция объединения множеств транзитивна (ассоциативность): 
· Пустое множество X является нейтральным элементом операции объединения множеств: 
· Таким образом булеан вместе с операцией объединения множеств является моноидом;
Операция пересечения множеств идемпотентна: 
Пересечение
Определение
Пусть даны два множества A и B.
Тогда их пересечением называется множество
! Гораздо реже используется обозначение AB.
Примеры
Пусть A = {1,2,3,4}, B = {3,4,5,6}. Тогда
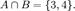
Свойства
· Пересечение множеств является бинарной операцией на произвольномбулеане 2 X;
· Операция пересечения множеств коммутативна: 
· Операция пересечения множеств транзитивна (ассоциативность): 
· Универсальное множество X является нейтральным элементом операции пересечения множеств: 
· Таким образом булеан вместе с операцией пересечения множеств является абелевой группой;
· Операция пересечения множеств идемпотентна: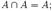 
· Если 
— пустое множество, то 
Дополнение
Определение
Пусть даны два множества A и B. Тогда их (теоретико-множественная) разность определяется следующим образом:
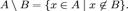
Примеры
· Пусть 
. Тогда 
· Пусть 
— множество всех вещественных чисел, 
— множество рациональных чисел, а 
— множество целых чисел. Тогда 
— множество всех иррациональных чисел, а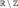 
— дробных.
Свойства
Пусть A, B, C — произвольные множества. Тогда
· 
· 
· 
· 
· 
· 
· 
· 
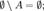
Алгебра множеств. Свойства операций.
Алгеброй множеств -называется пара 
, где 
— некоторая совокупность множеств, а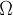 
— набор операций над множествами. Обычно полагают, что 
— множество всех подмножеств универсума 
.
| Свойства операций над множествами.
1. Ассоциативность: ,
2. Дистрибутивность: (AUB)∩C=(A∩C)U(B∩C), (A∩B)UC=(AUC)∩(BUC)
Поглощение: A U A = A, A ∩ A = A.
| 3. Существование универсальных границ:
А U 0 = A: A ∩ 0 = 0: A ∩ U = U: A ∩ U = A
4. Двойное дополнение (двойное отрицание):   , 
6. Законы двойственности или закон Де – Моргана
 , 
|
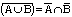Доказательства законов де Моргана для множеств.
Доказываем графически.
Имеем пересекающиеся множества А и В.
Законы де моргана: //!А = не А
!(А + В) =!А *!В;
!(А * В) =!А +!В.
Доказываем первый, второй доказывается аналогично.
Для начала рассмотрим множества А+В и!(А+В)
Это то, что у нас в левой части закона (выделено желтым).
Теперь, рассматриваем отдельно!А и!В
А теперь умножаем их и получаем правую часть закона (опять выделенно желтым)
Как видно, левая и правая части одинаковы. ЧТД.
Понятие мощности. Конечные и бесконечные множества.
Пусть n – число элементов данного множества А. Это число называется мощностью данного множества.
Конечным множеством называется множество, состоящее из конечного числа элементов. Примерами конечных множеств могут быть множество корней алгебраического уравнения n -й степени, множество букв русского алфавита.
Множество называется бесконечным, если оно состоит из бесконечного числа элементов. Таковы, например, множество всех натуральных чисел, множество точек окружности, множество прямых.