ой способ решения (метод потенциалов).

Задача №2

Тема: Транспортная задача

Задание

Имеются три пункта отправления А₁, А₂, А₃ однородного груза и пять пунктов В₁, В₂, В₃, В₄, В₅ его назначения. На пунктах А₁, А₂, А₃ груз находится в количестве а₁=90, а₂=30, а₃=110 тонн соответственно. В пункты В₁, В₂, В₃, В₄, В₅ требуется доставить соответственно b₁=10, b₂=60, b₃=50, b₄=40, b₅=70 тонн груза.

Расстояния в сотнях километров между пунктами отправления и назначения с_ij приведены в соответствующих клетках таблицы. Известна стоимость перевозки единицы груза из каждого пункта отправления в каждый пункт назначения (матрица D).

Составить план перевозок, при котором необходимо вывезти все запасы груза, полностью удовлетворить все потребности и обеспечить при этом минимум затрат на перевозку.

Указания: 1. Считать стоимость перевозок пропорциональной количеству груза и расстоянию, на которое груз перевозится. 2. Для решения задачи использовать методы: минимальной стоимости и потенциалов.

 

Решение.

Пункты отправления	Пункты назначения	Запасы
В1	В2	В3	В4	В5
А1						а1=90
А2						а2=30
А3						а3=110
	b1=10	b2=60	b3=50	b4=40	b5=70
Потребности

 

 

Ой способ решения (метод минимальной стоимости).

Суть метода состоит в том, что из всей таблицы стоимостей выбирают наименьшую и в эту клетку помещают меньшее из чисел а_iилиb_j.Затем из рассмотрения исключают либо строку (если запасы а_i выбраны), либо столбец (если потребитель B_jполностью удовлетворён). Из оставшейся части таблицы стоимостей снова выбирают наименьшую стоимость, и процесс распределения запасов продолжается таким же образом, пока все запасы будут распределены.

Сначала выбрали клетку А₁В₂, затем клетку А₁В₃ (из рассмотрения исключается первая строка), потом клетку А₃В₁(из рассмотрения исключается первый столбец). Далее рассматриваем клетки А₃В₃ и А₃В₅.

В оставшихся второй строчке и четвёртом столбце распределяем груз так, чтобы удовлетворить оставшихся потребителей.

Пункты Отправ- ления	Пункты назначения	Запа- сы
В1	В2	В3	В4	В5
А1						а1=90
А2						а2=30
А3						а3= =110
	b1=10	b2=60	b3=50	b4=40	b5=70
Потребности

 

Найдём общую стоимость составленного плана как сумму произведений объёмов перевозок на соответствующие стоимости в этих же клетках:

(ед. стоимости).

Ответ: план представлен таблицей, общая стоимость всех перевозок 670(ед.стоимости).

 

 

ой способ решения (метод потенциалов).

В качестве первоначального плана возьмём план, полученный методом минимальной стоимости

 

Пункты Отправ- ления	Пункты назначения	Запа- сы
В1	В2	В3	В4	В5
А1						а1=90
А2						а2=30
А3						а3= =110
	b1=10	b2=60	b3=50	b4=40	b5=70
Потребности

 

Критерий оптимальности. Чтобы план был оптимальным, необходимо выполнение следующих условий:

а) для каждой занятой клетки сумма потенциалов должна быть равна стоимости единицы перевозки груза, стоящей в этой клетке

;

б) для каждой незанятой клетки сумма потенциалов должна быть не больше стоимости единицы перевозки груза, стоящей в этой клетке

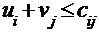или

Если хотя бы одна незанятая клетка не удовлетворяет последнему условию, то опорный план не является оптимальным, и его можно улучшить.

Таким образом, для проверки плана на оптимальность необходимо построить систему потенциалов.

 

1) Построение системы потенциалов для плана.

Для построения системы потенциалов используем условие для каждой занятой клетки. Систему потенциалов можно построить для невырожденного опорного плана, который содержит (m+n-1)занятых клеток, где m-число поставщиков, n-число потребителей. Для каждой занятой клетки можно составить уравнение (; ). Таких уравнений будет (m+n-1), а неизвестных (m+n). Уравнений на одно меньше, чем число неизвестных, поэтому система имеет бесчисленное множество решений и одному неизвестному придают произвольное значение (обычно нулевое). После этого определяются остальные потенциалы.

В таблице 7 занятых клеток (m+n-1=3+5-1=7), поэтому план невырожденный.

Выбираем строку, в которой имеется наибольшее число занятых клеток. Такая строка А₃, поэтому полагаем в этой строке потенциал u₃=0. Клетка А₃В₁ содержит стоимость с₃₁=2, для неё должно выполняться условие u₃+v₁=2, откуда следует потенциал v₁=2.Далее клетка А₃В₃: u₃+v₃=3, откуда v₃=3. Следующая клетка по этой строке А₃В₄, в которой u₃+v₄=5, с учетом u₃=0 имеем v₄=5. В клетке А₃В₅u₃+v₅=3,отсюда v₅=3. Для следующей занятой клетки А₂В₄:u₂+v₄=u₂+5=8, поэтому u₂=3. Далее.А₁В₃:: u₁+v₃=u₁+3=1, отсюда: u₁=-2.

Таким образом, системы потенциаловпостроена.

 

Поставщики	Потребители	Запасы
В1	В2	В3	В4	В5
v1=2	v2= 3	v3= 3	v4=5	v5=3
A1	u1=-2						а1=90
A2	u2=3						а2=30
A3	u3=0						а3=110
Потребности

 

 

2) Проверка выполнения условия оптимальности.

Для каждой незанятой клетки проверяем выполнение условия

Если для всех незанятых клеток выполняется это условие, то план оптимальный. Если для некоторых клеток , то план не является оптимальным. Тогда для этих клеток находим величину разности

и записываем в нижний левый угол этой клетки.

В клетке А₂В₂ нарушено условие оптимальности:

(в этой клетке цифра 2 в квадратике).

Итак, опорный план не является оптимальным.

3) Выбор клетки, в которую необходимо послать перевозку.

В транспортной задаче загрузке подлежит клетка, в которой не выполняется условие оптимальности. Поэтому клетку А₂В₂ необходимо сделать занятой.

4) Построение цикла и определение величины перераспределения.

 

Поставщики	Потребители	Запасы
В1	В2	В3	В4	В5
v1=2	v2= 3	v3= 3	v4=5	v5=3
A1	u1=-2		601	301			а1=90
A2	u2=3				308		а2=30
A3	u3=0			20	105		а3=110
Потребности

 

Отмечаем знаком (+) незанятую клетку А₂В₂. До этого в таблице было (m+n-1=3+5-1=7) занятых клеток, которые составляли базис. Теперь в таблице стало (m+n=3+5=8) занятых клеток (линейно зависимых), поэтому должен существовать замкнутый цикл. Намечаем его пунктиром, поочерёдно расставляем знаки (+) и (-) на поворотах, начиная с клетки А₂В₂.Из клетки А₂В₂ перемещаемся в клетку А₁В₂, затем в А₁В₃, потом в А₃В₃, далее в А₃В₄, следуем в А₂В₄, и наконец возвращаемся в А₂В₂

Цикл замкнулся.

Затем находим , где - перевозки, стоящие в вершинах цикла, отмеченные знаком . Величина определяет количество груза, которое надо перераспределить по циклу. Величина прибавляется к перевозкам, отмеченным знаком , и вычитается от перевозок, отмеченным знаком . Имеем . Следовательно, перевозку, равную 20 перемещаем в клетку А₂В₂, из клеток со знаком (-) отнимаем 20, а в клетки со знаком (+) прибавляем 20.

В результате получен новый опорный план, который снова подлежит проверке на оптимальность.

Поставщики	Потребители	Запасы
В1	В2	В3	В4	В5
v1=2	v2= 1	v3= 1	v4=5	v5=3
A1	u1=0						а1=90
A2	u2=3						а2=30
A3	u3=0						а3=110
Потребности

 

 

5) Изменение системы потенциалов.

Для клетки А₂В₂, в которой было нарушено условие оптимальности, нужно изменить систему потенциалов, но предварительно проверим третью строку: в занятых клетках потенциалы не трогаем, то есть u₃=0, v₁=2, v₄=5, v₅=3. Переходим ко второй строке: оставляем без изменения u₂=3, чтобы не нарушить равенство в клетке А₂В₄; теперь рассмотрим клетку А₂В₂, для неё , откуда следует . Итак, вторая строка по занятым клеткам выполнена. Теперь рассмотрим первую строку: клетка А₁В₂ 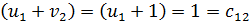, отсюда 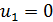; осталась последняя клетка А₁В₃

, откуда . Система потенциалов построена.

6) Проверка выполнения условия оптимальности

Далее проверяем незанятые клетки на оптимальность. Все клетки удовлетворяют условию оптимальности ,

следовательно, план оптимальный.

Найдём общую стоимость составленного плана как сумму произведений объёмов перевозок на соответствующие стоимости в этих же клетках:

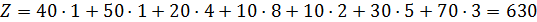(ед. стоимости).

Ответ: план представлен таблицей, общая стоимость всех перевозок 630(ед.стоимости).