Лекция № 4.
§1. Применениедифференциалакприближенномувычислениюзначенияфункции.
] задана функция y = f(x)
Запишем приращение этой функции: Δy = f’(x)Δx + α(Δx)Δx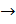 
Δy = dy + αΔx,
то есть дифференциал функции отличается от приращения функции на величину б/м высшего порядка малости относительно Δх 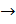если f'(x) ≠ 0, то αΔх – б/м высшего порядка малости относительно Δy, поэтому последнее слагаемое можно отбросить:
Δy ≈ dy
Пример: Найти sin31˚
sin31˚ = sin(30˚ + 1˚) = sin 30˚ + (sinx)’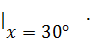 
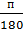= sin30˚ + cos30˚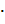 
= = 
+ 
+ 
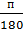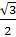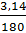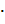= + 0,017 0,85 = 0,515
§2. Производныевысшихпорядков.
Опр.1Производнойn-огопорядка от функции f(x) def производная первого порядка от производной (n – 1)-го порядка и обозначается символом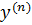 
или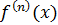 
:
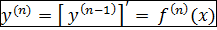
Замечание: производная до 3-го порядка включительно обозначается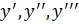 
. Производные четвертого, пятого и высших порядков иногда обозначаются римскими цифрами без скобок: 
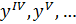или арабскими цифрами в скобках: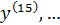 
Пример: Найти все производные от функции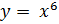 
Обобщенныеправиладифференцирования.
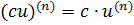
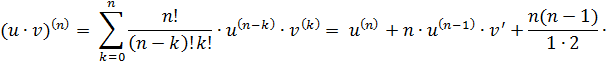
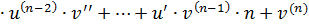
Дифференциалыразличныхпорядков
Опр.2Дифференциаломn-огопорядка def первый дифференциал от дифференциала (n-1)-го порядка:
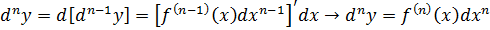
Таким образом: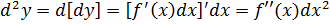 
Из определения дифференциалов разных порядков →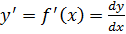 
; 
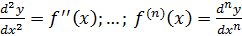
Замечания: 1)Все указанные выше формулы справедливы для случаев, когда «х» является независимой переменной 2) Для сложной функции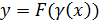 
дифференциал вычисляется:
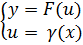
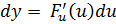
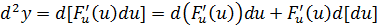, т.к. 
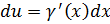или 
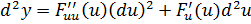, где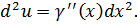 
Пример: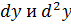 
сложной функции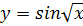 
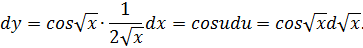
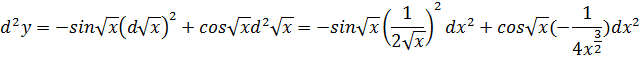
§3. Производныепараметрическизаданныхфункций.
] функция y от х задана параметрически:
Предположим, что эти функции имеют производные, а также функция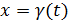 
имеет обратную 
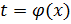, которая также имеет производную. Тогда функцию 
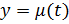можно рассматривать как сложную функцию.
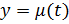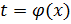, , t – промежуточный аргумент. Как сложная функция 
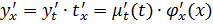(*). Тогда так как 
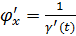(как обратная функция). Подставляя последнее равенство в (*), получим: 
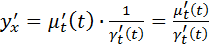или
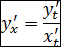
Отсюда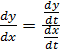 
. Аналогично, можно вывести производные высших порядков для параметрически заданных функций: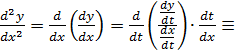 
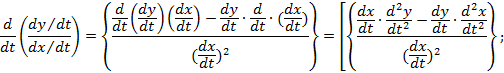
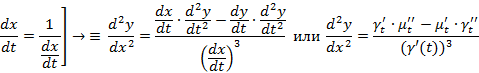
Пример: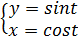 
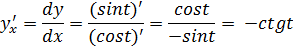
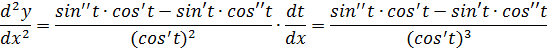
§4. Основныетеоремыдифференциальногоисчисления.
Опр.1 Функция y = f(x) достигает в точке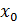 
локальногомаксимума (минимума), если существует окрестность этой точки 
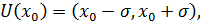на которой выполняется неравенство:
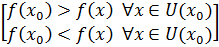
| y |
| y |
| max |
( )
|
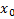| x |
| ()
|
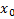| x |
| min |
Замечания: 1) Если функция направлена на [ a, b ] и достигает на нем extr в точке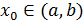 
, то точка 
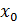является в то же время точкой локального min (max). 2) Если max или min достигается на концевых точках отрезка, то этот extr функции не будет локальным.
Теорема 1 (Ферма)
Если функция f(x) имеет производную в точке 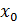и достигает в этой точке локального extr, то 
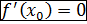(без доказательства).
Теорема 2 (Ролля)
Если функция f(x) непрерывна на отрезке [ a, b ], дифференцируема на интервале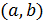 
и f(a) = f(b), то существует точка 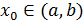такая, что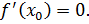 
Доказательство:
1) Если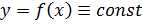 
на [ a, b ], то для всех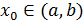 
.
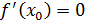2) ] 
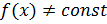на [ a, b ]. Т.к. f(x) - непрерывна на [ a, b ], то существует точка 
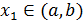, в которой функция достигает своего максимума на [ a, b ] и существует точка 
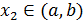, в которой достигается минимум (по т.Вейерштрасса). Обе точки не могут находиться на концах отрезка [ a, b ], иначе 
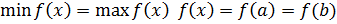и функция была бы постоянной на [ a, b ] → одна из точек 
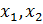принадлежит интервалу (a,b). Обозначим эту точку 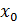. В ней достигается локальный extr. Кроме того, существует 
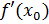(по условию) → по т.Ферма 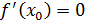. ч.т.д.
Замечания: 1) Т.Ролля теряет силу, если хотя бы в одной точке (a,b)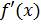 
не существует. 2) В теореме также нельзя заменить непрерывность на [ a, b ] на непрерывность на (a,b).
Геометрическийсмысл
| y |
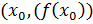, касательная в которой параллельна оси ОX.
| x |
| a |
| b |
Теорема 3 (Коши)
Если функции f(x) и g(x) непрерывны на [ a,b ] и дифференцируемы на (a,b) и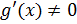 
в (a,b), то существует точка 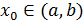такая, что
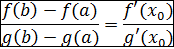
Доказательство:
1) Заметим, что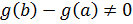 
, т.к. в противном случае по т.Ролля существовала бы точка 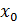такая, что 
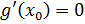(!!! условно). Введем вспомогательную функцию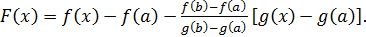 
В силу условия теоремы эта функция непрерывна на [ a,b ], дифференцируема на (a,b) и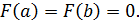 
Применяя т.Ролля получим, что существует точка 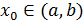, в которой 
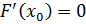. Но
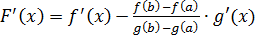→ подставив вместо x точку 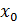, получим утв-е теоремы. ч.т.д.
Теорема 4 (о среднем) (Лагранжа)
] функция f(x) непрерывна на [ a,b ] и имеет производную на (a,b), тогда существует точка 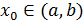, для которой выполняется равенство:
(*) 
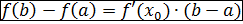
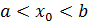
Доказательство: Если в условиях т.Коши принять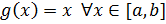 
, будем иметь 
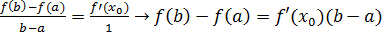ч.т.д.
Геометрический смысл.
Т.Лагранжа утверждает, что если f(x) есть непрерывная на [ a,b ] функция, дифференцируемая на (a,b), то на кривой y = f(x) существует точка такая, что касательная к кривой в этой точке параллельна хорде, стягивающей концы кривой (a,f (a)) и (b,f (b)).
Замечание: формула (*) def формулойконечныхприращений.