Лабораторная работа 2 «Эксплуатация и диагностика опор контактной сети»
Цель работы: ознакомиться со способами определения коррозионного состояния железобетонной опоры контактной сети
Порядок выполнения работы:
1) Изучить и составить краткий отчет о работе прибора АДО-3.
2) Изучить и решить задачу по методу минимального риска (согласно вариантам (по номеру в журнале)
3) Рассмотреть спец.вопрос о способах диагностики состояния опор (за исключением угла наклона).
П.п. 1 и 3 выполняются бригадой в количестве 5 человек.
П.2 выполняется индивидуально каждым студентом.
В результате необходимо сделать индивидуальный электронный отчет и прикрепить его в blackboard.
Метод минимального риска
При наличии неопределенности принятия решения применяют специальные методы, учитывающие вероятностную природу событий. Они позволяют назначать границу поля допуска параметра для принятия решения о диагностировании.
Пусть производится диагностика состояния железобетонной опоры вибрационным методом.
Вибрационный метод (рис 2.1) основан на зависимости декремента затухающих колебаний опоры от степени коррозии арматуры. Опора приводится в колебательное движение, например, при помощи троса оттяжки и сбрасывающего устройства. Сбрасывающее устройство калибруется на заданное усилие. На опоре устанавливается датчик колебаний, например акселерометр. Декремент затухающих колебаний определяется как логарифм отношения амплитуд колебаний:
 , (2.1)
, (2.1)
где А2 и А7 – амплитуды, соответственно второго и седьмого колебаний.


а) схема б) результат измерений
Рисунок 2.1 – Вибрационный метод
АДО-2М измеряет амплитуды колебаний 0,01... 2,0 мм частотой 1... 3 Гц.
Чем больше степень коррозии, тем быстрее затухают колебания. Недостатком метода является то, что декремент колебаний в большой степени зависит от параметров грунта, способа заделки опоры, отклонений технологии изготовления опоры, качества бетона. Заметное влияние коррозии проявляется лишь при значительном развитии процесса.
Задача стоит в выборе значения Хо параметра Х таким образом, чтобы при Х>Хо принимали решение о замене опоры, а при Х<Хо не проводили управляющего воздействия.
Условимся считать D1 – исправное состояние опоры, D2 – наличие коррозии. Тогда правило состоит в следующем:
 . (2.2)
. (2.2)
Декремент колебаний опоры зависит не только от степени коррозии, но и от множества других факторов. Поэтому можно говорить о некоторой области, в которой может находиться величина декремента. Распределения декремента колебаний для исправной и прокорродировавшей опоры показано на рис. 2.2.

Рисунок 2.2 - Плотность вероятности декремента колебаний опоры
Существенно, что области исправного D 1 и коррозионного D 2 состояний пересекаются и потому невозможно выбрать x0 так, чтобы правило (2.2) не давало бы ошибочных решений.
Ошибка первого рода - принятие решения о наличии коррозии (дефекта), когда в действительности опора (система) находится в исправном состоянии.
Ошибка второго рода - принятие решения об исправном состоянии, тогда как опора (система) прокорродировала (содержит дефект).
Вероятность ошибки первого рода равна произведению вероятностей двух событий: вероятности наличия исправного состояния и вероятности того, что x > x0 при исправном состоянии:
 , (2.3)
, (2.3)
где P(D1) = P1 - априорная вероятность нахождения опоры в исправном состоянии (считается известной на основании предварительных статистических данных).
Вероятность ошибки второго рода:
 , (2.4)
, (2.4)
где P(D2) = P2 - априорная вероятность коррозии (дефекта), P2 = 1 – P1.
Если известны цены ошибок первого и второго рода c и y соответственно, то можно записать уравнение для среднего риска:
 . (2.5)
. (2.5)
Найдем граничное значение x0 для правила (2.5) из условия минимума среднего риска. Подставляя (2.6) и (2.7) в (2.8) дифференцируя R(x) по x0, приравняем производную нулю:
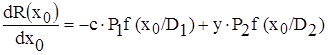 = 0, (2.6)
= 0, (2.6)
или
 . (2.7)
. (2.7)
Это условие для нахождения двух экстремумов - максимума и минимума. Для существования минимума в точке x = x0 вторая производная должна быть положительной:
 . (2.8)
. (2.8)
Это приводит к следующему условию:
 . (2.9)
. (2.9)
Если распределения f(x/D1) и f(x/D2) одномодальные, то при:
 (2.10)
(2.10)
условие (4.58) выполняется.
Если плотности распределений параметров исправной и неисправной (системы) подчинены закону Гаусса, то они имеют вид:
 , (2.11)
, (2.11)
 . (2.12)
. (2.12)
Условия (2.7) в этом случае принимает вид:
 . (2.13)
. (2.13)
После преобразования и логарифмирования получаем квадратное уравнение
 , (2.14)
, (2.14)
где a =  ;
;
b =  ;
;
c =  .
.
Решая уравнение (2.14) можно найти такую величину x0, при которой достигается минимум риска.
Исходные данные:
Исправное состояние:
Математическое ожидание: 
Вероятность исправного состояния системы: 
Среднеквадратичное отклонение: 
Приведенные затраты на исправное состояние: 
Неисправное состояние:
Математическое ожидание:  ;
;
Вероятность неисправного состояния системы: 
Среднеквадратичное отклонение: 
Приведенные затраты на неисправное состояние: 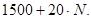
Пример решения:
Таблица 2.1 – Исходные данные
| Номер варианта | 
| 
| 
| 
| 
| У | Р1 | 
|
| N | 0,1 | 0,01 | 0,3 | 0,015 | 0,989 | 0,011 |







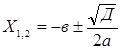

Вывод:
При  достигается минимум риска.
достигается минимум риска.