EX = a
DX = σ2
13. Функция распределения и ее свойства
Функция распределения — функция, характеризующая распределение случайной величины (вероятность того, что случайная величина примет меньшее значение)
P(X < x) = P(A)
Свойства:
1. Функция распределения есть неубывающая функция
2. На минус бесконечности функция распределения равна нулю F(-∞) = 0
3. На плюс бесконечности функция распределения равна единице F(+∞) = 1
прерывная (ступенчатый график)
равномерная (график y=kx+b)
14. Эмпирическая функция распределения
Эмпирическая функция распределения – полученная на опыте
nx – одно из наблюдаемых значений
n – сумма выборки (сумма всех наблюденных значений)
Свойства:
Значения эмпирической функции принадлежат отрезку [0,1].
Она неубывающая функция.
Если 
– наименьшее наблюдаемое значение, то F(X) = 0 при 
,
если 
– наибольшее, то F(X) = 1 при 
.
15. Полигон и гистограмма
Для наглядности строят различные графики статистического распределения, в частности, полигон и гистограмму.
Полигоном частот называют ломаную линию, отрезки которой соединяют точки 
.
В случае непрерывного признака строится гистограмма, для чего интервал, в котором заключены все наблюдаемые значения признака, разбивают на несколько частичных интервалов длиной h и находят для каждого частичного интервала 
– сумму частот вариант, попавших в i–й интервал.
Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которой служат частичные интервалы длиною h, а высоты равны отношению 
. (аналог функции плотности вероятностного распределения). Площадь одного прямоугольника - вероятность
16. Функция плотности вероятностного распределения и ее свойства
Производная от функции распределения – функция плотности вероятностного распределения.
Свойства:
1. Площадь прямоугольника на графике функции = 1
2. f(x) – неотрицательная функция т.е. f(x) ≥ 0;
17. Биномиальное распределение
Биномиальное распределение - распределение количества «успехов» в последовательности из N независимых случайных экспериментов, таких что вероятность «успеха» равна p, а неудачи - q.
биномиальное распределение – появляется в схеме независимых испытаний Бернулли – в каждом опыте либо успех (p) либо неудача (q)
| … | n |
- опыты
C вероятностью: 
Где 
- 
– биномиальный коэффициент.
EX = np
DX = npq
0 < p < 1
q = 1 – p
18. Теорема и распределение Пуассона
Распределение Пуассона - это частный случай биномиального распределения для редких событий)
| … | n |
с вероятностью: 
(теорема Пуассона: если n устремить к ∞, а p к 0, тогда для любого k вероятность получить успех при n испытаниях по схеме Бернулли стремится к этой формуле)
EX = λ
DX = λ
19. Нормальное вероятностное распределение
нормальное вероятностное распределение – куполообразный график
EX = a
DX = σ2
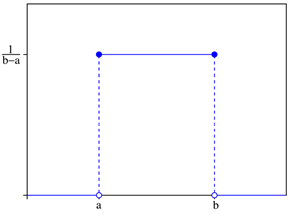
20. Равномерное распределение
Непрерывное равномерное распределение характеризуются тем, что вероятность любого интервала зависит только от его длины
21. Локальная предельная теорема Муавра-Лапласа
Предельные теоремы – совокупность теорем, говорящих о том, что все распределения сводятся к нормальному.