Лекция №4
|
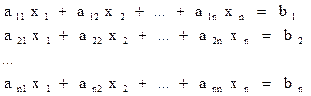 |
 Дана система линейных уравнений (СЛАУ) с n неизвестными:
Дана система линейных уравнений (СЛАУ) с n неизвестными:
В матричной форме записи система (4.1) имеет вид:
 (4.2)
(4.2)
где: n – порядок системы;
 – матрица коэффициентов системы;
– матрица коэффициентов системы;
 – вектор свободных членов;
– вектор свободных членов;  – вектор неизвестных;
– вектор неизвестных;
В свернутой форме записи СЛАУ имеет вид:

 (4.3)
(4.3)
Система называется обусловленной (не вырожденной, не особенной), если определитель системы DA ¹ 0, и тогда система (4.1) имеет единственное решение.
Система называется не обусловленной (вырожденной, особенной), если DA = 0, и тогда система (4.1) не имеет решений или имеет бесконечное множество решений.
На практике коэффициенты системы aij и свободные члены bi часто задаются приближенно, с некоторой неустранимой погрешностью. Поэтому, кроме существования и единственности решения СЛАУ, важно еще знать, как влияет такая погрешность на получаемое решение.
Система называется плохо обусловленной, если неустранимая погрешность оказывает сильное влияние на решение; у таких систем определитель близок, но не равен 0.
Рассмотрим пример плохо обусловленной системы.
 Дана система
Дана система 

Решение  ;
; 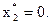
Пусть b2 имеет неустранимую погрешность  %.
%.
Если b2 = 1,01, то 
Если b2 = 0,99, то 
Решение изменяется очень сильно, следовательно, система плохо обусловлена, о чем говорит значение её определителя.
Рассмотрим геометрическую иллюстрацию обусловленности СЛАУ на примере системы двух уравнений с двумя неизвестными:
 a11 x1+ a12 x2 = b1 уравнение (I)
a11 x1+ a12 x2 = b1 уравнение (I)
a21 x1+ a22 x2= b2 уравнение (II)
 |
Рис. 4.1. Геометрическая иллюстрация обусловленности СЛАУ.
Каждому уравнению в плоскости (x1,x2) соответствует прямая, а точка пересечения этих прямых является решением этой системы. Если ΔA = 0, то наклоны прямых одинаковы, и они либо параллельны (т.е. не имеют решения), либо совпадают (имеют бесконечное множество решений). Если ΔA ¹ 0, то прямые имеют единственную точку пересечения.
Но если система плохо обусловлена (∆А≈0), даже незначительное изменение одного из коэффициентов приведет к сильному изменению решения системы, т.к. прямые почти параллельны.
Способы решения линейных уравнений разделяют на 2-е основные группы:
1) Точные методы (прямые)- представляют собой конечные алгоритмы вычисления корней системы (правило Крамера, метод Гаусса, метод обратной матрицы). Дают решение в процессе конечного числа элементарных арифметических операций, зависящих от вычисляющей схемы и размера матрицы.
2) Итерационные методы- позволяют получать корни системы с заданной точностью на основе сходящегося бесконечного процесса (метод итерации, метод Зейделя) – как предел итерационного процесса. Его эффективность зависит не только от сходимости, но и от скорости сходимости.
В силу неизбежных округлений результата даже точные методы являются приближенными. При использований итерационных методов добавляется еще погрешность метода. Эффективность итерационных методов существенно зависит от удачного выбора начального приближения и быстроты сходимости процесса.
Для решения СЛУ широко применяются прямые и итерационные методы. Область применения некоторых из них показана в таблице.
| Тип | Название метода | Число арифметических действий (при n = 20) | Область примененения |
| Прямые | Формулы Крамера | ~  ( (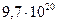 ) )
| n<5 |
| Исключения Гаусса | ~  (5733) (5733)
| n<200 | |
| Итерационные | Простых итераций | ~ n² на каждой итерации (400n) | до 105 |
| Гаусса-Зейделя |
Современная супер-ЭВМ имеет производительность 30 терафлоп – 30·1012 операций с вещественными числами в секунду. Такой машине для решения СЛАУ для n=20 по формуле Крамера требуется:
 года.
года.
На решение СЛУ прямым методом сильное влияние оказывает погрешность округления, т.к. требуется огромное количество арифметических действий.
На решение СЛАУ итерационным методом погрешность округления практически не влияет, но не всегда удается обеспечить сходимость итерационного процесса.
4.2. Метод исключений Гаусса.
Решим рассмотренную ранее систему (пример 4.1) методом исключения Гаусса.
Пример 3.2. Решение проводиться в два этапа.
1 этап Прямой ход - матрица A преобразуется к треугольному виду: путем эквивалентных линейных преобразований уравнений системы поддиагональные коэффициенты матрицы А обнуляются.
 x1 + 5×x2 - x3 = 2
x1 + 5×x2 - x3 = 2
x1 2×x3 = -1
2×x1 - x2 – 3×x3 = 5
Исключим x1 из 2-го и 3-го уравнения: ко 2-му уравнению прибавим 1-ое, умноженное на (-1); к 3-му уравнению прибавим 1-ое, умноженное на (-2).
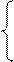 x1 + 5×x2 - x3 = 2
x1 + 5×x2 - x3 = 2
- 5×x2 + 3×x3 = -3
- 11×x2 – x3 = 1
Исключим x2 из 3-го уравнения: к 3-му уравнению прибавим 2-ое, умноженное на (-11/5). Полученный вид системы после прямого хода
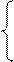 x1 + 5×x2 - x3 = 2
x1 + 5×x2 - x3 = 2
- 5×x2 + 3×x3 = -3
– 38/5×x3 = 38/5
2 этап Обратный ход - вычисляются значения неизвестных, начиная с последнего уравнения:
x3* = -1
-5×x2 + 3×x3*=-3 Þ x2*=(3 + 3×x3*)=(3 + 3×(-1))=0
x1 +5×x2* - x3*=2 Þ x1*=2 + 5×x2* + x3*=2 + 5×0 + (-1)=1
Полученное решение нужно обязательно проверить, подставив в исходную систему!
Словесное описание алгоритма метода исключения Гаусса. Схема алгоритма приведена на рисунках 4.1-4.6.
Алгоритм прямого хода:
Шаг 1. Примем k=1
Шаг 2. Выбираем рабочую строку.
Если akk ≠ 0, то k-ая строка – рабочая.
Если нет, меняем k-ю строку на m-ю (n≥m>k), в которой amk ≠ 0,  . Если такой строки нет, система вырожденная, решение прекратить.
. Если такой строки нет, система вырожденная, решение прекратить.
Шаг 3. Для строк i=k+1, k+2, …, n вычисляются новые значения коэффициентов.
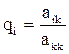 ,
,  ,
,  и новые правые части
и новые правые части 
Шаг 4. Увеличиваем k = k + 1. Если k = n, прямой ход завершен, иначе алгоритм повторяется со второго шага.
Получаем верхнюю треугольную матрицу А:
 ,
, 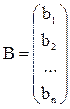
Алгоритм обратного хода:
Шаг 1. Вычислим 
Шаг 2. Вычислим:
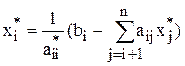 ,
, 
Для контроля правильности решения нужно считать невязки δi по формуле
δi  ,
,  (4.5)
(4.5)
Если невязки велики, задача решена неверно. Причиной может быть сбой машины (крайне редко), ошибки в программе, погрешность округления (при большом n и когда DA = detA = 0- система плохо обусловлена).
 |
Рис. 4.1. Основной алгоритм решения СЛУ методом исключения Гаусса.
Разновидности метода Гаусса:
а) Метод Гаусса - Краута с выбором главного элемента в столбце. Метод Краута является одним из вариантов метода Гаусса, когда ведущий элемент на каждом шаге «прямого хода» выбирается наибольшим из элементов преобразуемого столбца при сведении А к верхнетреугольной.
В алгоритме прямого хода на шаге 2 рабочая строка выбирается из условия
 ,
,
т.е. рабочей выбирается та строка, в которой находится наибольший по модулю коэффициент k-го столбца, расположенный на главной диагонали и под ней.
Если простой метод Гаусса требует 0.8n3+1.8n2+0.4n условных арифметических операций, то метод Краута- 1.43n3+28n2+6.36n условных арифметических операций, т.е. их большего числа, но обеспечивает исключение случайного деления на 0 и устойчивой вычислительной схемы. Т.е. в обычном методе Гаусса большая погрешность полученного решения может быть обусловлена малостью ведущего элемента ( ).
).
б) Метод Гаусса-Жордана. В результате прямого хода приводит матрицу коэффициентов к диагональному виду.
В алгоритм прямого хода нужно внести следующие изменения:
- на шаге 3 
- на шаге 4 прямой ход завершиться при достижении условия k>n.
 | |||
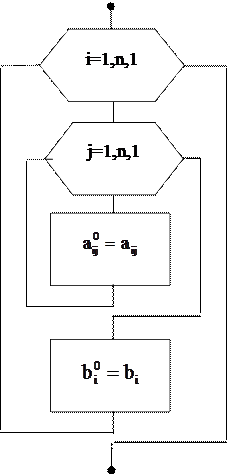 | |||
Рис. 3. Алгоритм запоминания коэффициентов.
Рис. 4.2. Алгоритм прямого хода
 | |||
 |
Рис. 4.6. Алгоритм расчета невязок
Рис. 4.5. Алгоритм обратного хода.
Вид матрицы коэффициентов после прямого хода

Упрощается обратный ход: xi =bi / ai,i, i =1,2,…,n
Недостаток метода – увеличение общего числа действий, и соответственно, влияния погрешности округления.
Нужно подчеркнуть, что для вычисления значения определителя квадратной матрицы можно использовать алгоритм прямого хода: для треугольной или диагональной квадратной матрицы определитель равен произведению элементов главной диагонали.
Метод простых итераций.
Рассмотрим особенности решения СЛУ методом простых итераций на примере.
Пример 4.3. Требуется найти решение системы с точностью ε=0,001.
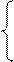 x1 + 5×x2 - x3 = 2
x1 + 5×x2 - x3 = 2
x1 2×x3 = -1
2×x1 - x2 – 3×x3 = 5
Приведем систему к новому, каноническому виду метода простых итераций. Для этого нужно преобразовать исходную систему так, чтобы в каждой строке новой матрицы А коэффициент, расположенный на главной диагонали, превышал по абсолютной величине сумму абсолютных значений остальных коэффициентов в этой сроке.
При выполнении эквивалентных линейных преобразований системы нужно соблюдать следующие требование: каждое уравнение исходной системы должно участвовать хотя бы в одном преобразовании.
В первом уравнении исходной системы коэффициент при х2 больше суммы модулей других коэффициентов: 5> 1+1. Поэтому это уравнение в новой системе нужно записать вторым уравнением. Для получения нового первого уравнения можно второе уравнение умножить на 2 и сложить с третьим уравнением. Для получения нового третьего уравнения можно из третьего уравнения вычесть второе.
В итоге описанных преобразований получиться следующая система:


Важно отметить, что подобные преобразования не меняют решения системы.
Выразим явно из каждого нового уравнения очередное неизвестное – получим формулы итерационного процесса.


Возьмем любое начальное приближение  , например
, например  .
.
Вычислим новое приближение решения  , подставив в правую часть
, подставив в правую часть 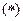 начальное приближение:
начальное приближение:


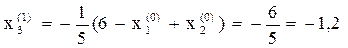
Оценим достигнутую точность δ по формуле:

Итерационный процесс нужно продолжить, т.к. δ > ε.
Вычислим второе приближение  , подставив в правую часть
, подставив в правую часть  первое приближение:
первое приближение:


Третье приближение:

Четвертое приближение:
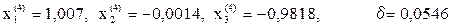
Очевидно, что итерационный процесс сходиться, т.к. значение δ монотонно убывает. Для достижения требуемой точности ε=0,001 потребуется еще несколько итераций.
Скорость сходимости зависит от уровня преобладания значений диагональных коэффициентов.
Основные расчетные зависимости метода простых итераций:
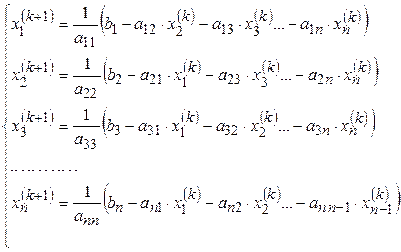 (4.6)
(4.6)
Формула итерационного процесса:
 ,
,  (4.7)
(4.7)
где: k = 0,1, 2, … – номер приближения.
 – начальное приближение,
– начальное приближение,  ;
;
Условия завершения итерационного процесса (критерий сходимости):
d£e (4.8), где e – требуемая точность; 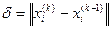 – оценка достигнутой точности, в зависимости от нормы
– оценка достигнутой точности, в зависимости от нормы  может иметь вид:
может иметь вид:
 ,
,
 или
или  (4.9)
(4.9)
Условие сходимости итерационного процесса (условие преобладания диагональных коэффициентов):
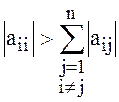
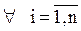 (4.10)
(4.10)
Схема алгоритма метода представлена на рис. 4.7.
Если в полученных результатах значения δ > e и k > kmax, то задача не решена, т.е. x(1:n) не является решением системы. Необходимо проверить условия сходимости или увеличить kmax.
Метод Гаусса-Зейделя
В формуле итерационного процесса метода простых итераций (4.7) к моменту вычисления xi(k) уже вычислены значения x1(k),x2(k),...,xi-1(k).
Очевидно, что эти значения в большинстве случаев ближе к решению и их можно использовать для вычисления xi(k). Исходя из этого, Гаусс и Зейдель предложили видоизмененную формулу итерационного процесса
 (4.11)
(4.11)
Условие завершения итерационного процесса (4.8,4.9) и условия сходимости (4.10) справедливы и для данного метода. Поэтому схема алгоритма Гаусса-Зейделя отлична только формулой расчета нового приближения:
 (4.12)
(4.12)
Развернутый вид расчетной формулы итерационного процесса (4.11) метода Зейделя:

Вычисление первого и второго приближения примера  методом Зейделя:
методом Зейделя:
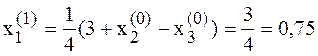

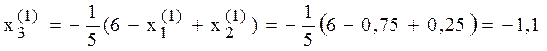



Метод Зейделя, как правило, позволяет достичь требуемой точности ε за меньшее число итераций, т.е. имеет лучшую сходимость.
Достоинства итерационных методов:
1. Погрешность округления не накапливается от итерации к итерации.
2. Число итераций при n>100 обычно меньше n, поэтому общее число действий меньше n3, т.е. меньше, чем в методе исключений Гаусса.
3. Не требуется большой объем памяти.
4. Итерационные методы особенно выгодны для систем с большим количеством нулевых коэффициентов (систем с разряженной итерацией). Методы исключения наоборот: чем больше нулей, тем чаще требуется выбирать новую рабочую строку.
Недостаток - не всегда можно обеспечить сходимость итерационного процесса. С увеличением размерности системы труднее выполнить линейные преобразования для обеспечения сходимости.
 |
Рис. 4.7. Схема алгоритма метода простых итераций