МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ ТОРГОВО-ЭКОНОМИЧЕСКИЙ УНИВЕРСИТЕТ
(РГТЭУ)
ИВАНОВСКИЙ ФИЛИАЛ
Кафедра Математики, экономической информатики
и вычислительной техники
МАТЕМАТИКА
Контрольная работа №2
Для студентов 1 курса заочного отделения
Направления 100700 «Торговое дело»
Профили Коммерция, Товароведение и экспертиза товаров
Иваново, 2014
Правила выбора варианта контрольного задания, оформления и зачета контрольных работ
Студент 1 курса заочной формы обучения по направлению 080200.62 «Менеджмент» выполняет по Математике две контрольные работы. Контрольные работы должны быть оформлены в соответствии с настоящими правилами. Работы, выполненные без соблюдения этих правил, не зачитываются и возвращаются студенту для переработки.
Контрольную работу следует выполнять в обыкновенной ученической тетради чернилами любого цвета, кроме красного, оставляя поля для замечаний рецензента.
На обложке тетради должны быть разборчиво написаны фамилия, имя, отчество студента, учебный шифр (номер студенческого билета), название дисциплины (Математика), домашний адрес и телефон студента. В конце работы следует поставить дату ее выполнения и расписаться.
В работу должны быть включены все задачи, указанные в задании, строго по своему варианту. Контрольные работы, содержащие не все задания, а также содержащие задачи не своего варианта, не зачитываются.
Номер варианта выполняемого задания совпадает с последней цифрой учебного шифра студента. Последняя цифра номера задания совпадает с номером варианта. Например, вариант № 4 содержит задания 4, 14, 24, 34, 44, 54. Решение задач надо располагать в порядке номеров, указанных в задании, сохраняя номера задач. Если несколько задач имеют общую формулировку, то при переписывании общие условия заменяются конкретными данными.
|
|
Решения задач надо оформлять аккуратно, подробно объясняя все действия и используемые формулы, а так же делая необходимые чертежи.
Регистрация и учет контрольных работ осуществляется в Учебном отделе заочной формы обучения (пр. Ленина, 43, комната 308)..
Срок проверки работ - 10 дней. Студенты обязаны сдавать письменные работы не позднее, чем за две недели до начала экзаменационной сессии. В противном случае они не будут допущены к зачетам и экзаменам.
Зачтенная контрольная работа остается у преподавателя. Незачтенная контрольная работа возвращается в Учебную часть заочного отделения, откуда ее должен взять студент на доработку. После получения прорецензированной незачтенной работы студент должен исправить все отмеченные рецензентом ошибки и недочеты и выполнить все его рекомендации. Если рецензент предлагает внести в решение задач те или иные исправления или дополнения и прислать их для повторной проверки, то это надо сделать в короткий срок. В случае незачета работы и отсутствия прямого указания рецензента на то, что студент может ограничиться представлением исправленных решений отдельных задач, вся работа должна быть выполнена заново. При высылаемых исправлениях должна находиться прорецензированная работа и рецензия на нее. В связи с этим рекомендуется при выполнении контрольной работы оставлять в конце тетради несколько чистых листов для всех дополнений и исправлений в соответствии с указаниями рецензента. Вносить исправления в сам текст работы после ее рецензирования запрещается.
|
|
Контрольная работа № 2 по Математике
Линейная алгебра с элементами аналитической геометрии
1 - 10. В декартовой прямоугольной системе координат даны координаты вершин пирамиды ABCD. Постройте чертеж и решите следующие задачи:
а) докажите, что система векторов 
линейно независима;
б) постройте вектор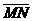 
, где M и N - середины ребер AD и BC соответственно, найдите его координаты и его разложение по базису 
;
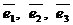в) найдите длину ребра AB;
г) вычислите величину угла между ребрами AB и AC;
д) напишите уравнение прямой АВ;
е) составьте уравнение плоскости АВС;
ж) напишите уравнение высоты, опущенной из вершины D на плоскость АВС.
1. A(1,-1,0), B(2,3,1), C(-1,1,1), D(4,-3,5).
2. A(2,0,-1), B(1,1,1), C(4,6,6), D(-1,2,3).
3. A(-3,1,1), B(0,-4,-1), C(5,1,3), D(4,6,-2).
4. A(1,1,4), B(2,1,2), C(1,-1,2), D(6,-3,8).
5. A(2,1,-4), B(-3,-5,6), C(0,-3,-1), D(-5,2,-8).
6. A(3,0,1), B(1,3,0), C(4,-1,2), D(-4,3,5).
7. A(3,0,-1), B(-1,-2,-4), C(-1,2,4), D(7,-3,1).
8. A(2,-2,1), B(1,2,-1), C(1,0,2), D(2,1,0).
9. A(1,-1,1), B(2,1,-1), C(-2,0,3), D(2,-2,-4).
10. A(0,1,-1), B(-3,0,1), C(1,2,0), D(1,-1,2).
11 – 20. При выполнении плана товарооборота магазин должен продать товары трех видов в количествах а11, а12, а13 (тыс. штук) соответственно. Если продавать эти товары в количествах а21, а22, а23 (тыс. штук) соответственно, то план товарооборота будет перевыполнен в полтора раза. Если же товары продать в количествах а31, а32, а33 (тыс. штук) соответственно, то выполнение плана составит лишь 75%.
|
|
Постройте математическую модель задачи и определите стоимость единицы товара каждого вида, если план товарооборота составляет Q тыс. руб.
Решите задачу:
а) методом Крамера;
б) методом Гаусса;
в) методом с использованием обратной матрицы.
План товарооборота магазина Q (тыс. руб.) и значения аij (в виде матрицы) даны ниже.
11. Q = 16, 
; 16. Q = 28,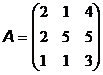 
;
12. Q = 18, 
; 17. Q = 36,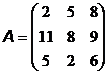 
;
13. Q = 20, 
; 18. Q = 42, ;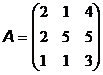
14. Q = 24,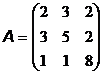 
; 19. Q = 32, 
;
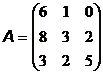15. Q = 80, 
; 20. Q = 12,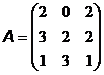 
.
Теория вероятностей
21. Два стрелка стреляют по мишени. Вероятность попадания в цель при одном выстреле для первого стрелка равна 0,6, а для второго - 0,9. Найти вероятность того, что при одном залпе в мишень попадут:
а) только первый стрелок; б) оба стрелка.
22. Вероятность безотказной работы в течение гарантийного срока для первого прибора составляет 0,8, а для второго - 0,95. Какова вероятность того, что в течение гарантийного срока окажутся работоспособными:
а) только второй прибор; б) хотя бы один прибор.
23. Прибор состоит из двух узлов, которые во время работы могут независимо друг от друга выходить из строя. Вероятность безотказной работы первого узла 0,75, а второго - 0,8. Найти вероятность того, что во время гарантийного срока будут работать исправно:
а) только один узел; б) оба узла.
24. Студент знает 24 из 30 вопросов по первому разделу и 32 из 35 вопросов по второму разделу курса. На экзамене ему случайным образом предлагается по одному вопросу из каждого раздела. Какова вероятность того, что студент ответит правильно:
а) только на один вопрос; б) хотя бы на один вопрос.
25. В магазине 20 цветных и 30 черно-белых телевизоров. Дополнительной регулировки требуют 2цветных и 6 черно-белых телевизора. Наугад взяли по одному телевизору из каждой группы. Найти вероятность того, что регулировки требуют:
а) только черно-белый телевизор; б) оба телевизора.
26. Проверкой качества занимаются два контролера - контролер ОТК на заводе и товаровед торгового предприятия. Вероятность выявления дефекта контролером ОТК равна 0,8, товароведом - 0,95. Найти вероятность того, что дефект выявит:
а) хотя бы один проверяющий; б) только товаровед.
27. Имеется 12 единиц товара в одинаковых упаковках. Известно, что из них 4 единицы первого сорта. Вычислите вероятность того, что среди двух наугад отобранных друг за другом единиц товара:
а) хотя бы одна первого сорта; б) только одна первого сорта.
28. В группе из 25 студентов 6 слабоуспевающих. Из группы наугад выбирают два человека. Какова вероятность того, что среди них:
а) только один слабоуспевающий; б) нет слабоуспевающих.
29. Имеется 7 радиоламп, среди которых 3 неисправные, на вид не отличающиеся от исправных. Наугад выбирают друг за другом две лампы. Какова вероятность того, что:
а) обе лампы окажутся исправными; б) хотя бы одна из них неисправная.
30. Из 40 вопросов студент знает 35. На экзамене ему случайным образом предлагается два вопроса. Какова вероятность того, что студент ответит правильно:
а) на оба вопроса; б) хотя бы на один вопрос.
31. Два специалиста ОТК проверяют качество выпускаемых изделий, причем каждое изделие с одинаковой вероятностью может быть проверено любым из них. Вероятность выявления дефекта первым специалистом равна 0,8, а вторым – 0,9. Из массы проверенных изделий наугад выбирается одно. Оно оказалось с дефектом. Какова вероятность того, что ошибку допустил второй контролер?
32. В двух одинаковых коробках находятся карандаши «Конструктор». Известно, что 1/3 карандашей в первой коробке и 1/4 карандашей во второй коробке характеризуются твердостью ТМ. Наугад выбирается коробка и из нее один карандаш. Он оказался твердости ТМ. Какова вероятность того, что он из первой коробки?
33. Товаровед плодоовощной базы определяет сорт поступившей от постоянного поставщика партии яблок. Известно, что 40% выращенного поставщиком урожая составляют яблоки первого сорта. Вероятность того, что товаровед совершит ошибку в установке сорта, проверяя первосортную партию, равна 0,15, а при проверке непервосортной партии вероятность такой ошибки 0,2. Какова вероятность того, что товаровед неправильно установит сорт партии яблок?
34. Магазин получил две равные по количеству партии одноименного товара. Известно, что 25% первой партии и 40% второй партии составляет товар первого сорта. Какова вероятность того, что наугад выбранная единица товара будет не первого сорта?
35. Укупорка банок производится двумя автоматами с одинаковой производительностью. Доля банок с дефектом укупорки для первого автомата составляет 1%, а для второго 0,5%. Какова вероятность того, что взятая наугад банка будет иметь дефект укупорки?
36. В магазин поступил одноименный товар, изготовленный двумя предприятиями. С первого предприятия поступило 150 единиц, из них 30 единиц первого сорта, а со второго предприятия 200 единиц, из них 50 единиц первого сорта. Из общей массы наугад выбирается одна единица. Она оказалась первого сорта. Какова вероятность того, что она изготовлена на первом предприятии?
37. Покупатель может приобрести нужный ему товар в двух магазинах. Вероятности обращения в каждый магазин зависят от их местоположения и равны 0,3 и 0,7. Вероятность того, что к приходу покупателя нужный ему товар не будет распродан, равна 0,8 для первого магазина и 0,4 – для второго. Какова вероятность того, что покупатель приобретет нужный ему товар?
38. Два контролера производят оценку качества выпускаемых изделий. Вероятность того, что очередное изделие попадет на проверку к первому контролеру, равна 0,55, а ко второму контролеру – 0,45. Первый контролер выявляет дефект с вероятностью 0,8, а второй с вероятностью 0,9. Найти вероятность того, что при проверке не правильно будет оценено качество изделия.
39. Пассажир может приобрести билет в одной из двух касс. Вероятность обращения в первую кассу составляет 0,4, а во вторую 0,6. Вероятность того, что к приходу пассажира нужные ему билеты будут распроданы, равна 0,35 для первой кассы и 0,7 для второй. Пассажир посетил одну из касс и приобрел билет. Какова вероятность того, что он приобрел его во второй кассе?
40. В магазин поступила обувь от двух поставщиков. Количество обуви, поступившей от первого поставщика в два раза больше, чем от второго. Известно, что в среднем 20% обуви от первого поставщика и 35% обуви от второго поставщика имеют разные дефекты отделки. Из общей массы наугад отбирают одну упаковку с обувью. Оказалось, что она не имеет дефекта отделки. Какова вероятность того, что ее изготовил первый поставщик?
41 - 50. Закон распределения дискретной случайной величины Х задан в таблице. Выполните задания:
* вычислите неизвестную вероятность р;
* определите математическое ожидание М(Х),дисперсию D(X) и среднее квадратическое отклонение s (Х).
* Найдите функцию распределения F(x) и постройте ее график.
| Номер | Значения xi случайной величины Х | ||||||
| задачи | -2 | -1 | |||||
| 41. | 0,01 | р | 0,23 | 0,28 | 0,19 | 0,11 | 0,06 |
| 42. | 0,20 | 0,31 | 0,24 | р | 0,07 | 0,04 | 0,01 |
| 43. | 0,04 | 0,08 | 0,32 | 0,31 | 0,15 | 0,08 | р |
| 44. | 0,42 | 0,23 | р | 0,10 | 0,06 | 0,03 | 0,01 |
| 45. | р | 0,29 | 0,12 | 0,15 | 0,21 | 0,16 | 0,04 |
| 46. | 0,05 | 0,12 | 0,18 | 0,30 | р | 0,12 | 0,05 |
| 47. | 0,06 | р | 0,12 | 0,24 | 0,33 | 0,14 | 0,03 |
| 48. | 0,16 | 0,25 | 0,25 | 0,16 | 0,10 | р | 0,03 |
| 49. | 0,02 | 0,38 | 0,30 | р | 0,08 | 0,04 | 0,02 |
| 50. | 0,08 | 0,10 | 0,14 | 0,17 | 0,18 | 0,19 | р |
51. По данным телеателье установлено, что в среднем 20% цветных телевизоров выходят из строя в течение гарантийного срока. Какова вероятность того, что из 225 проданных цветных телевизоров будут работать исправно в течение гарантийного срока
а) 184 телевизора; б) от 172 до 184 телевизоров.
52. При оценке качества продукции было установлено, что в среднем третья часть выпускаемой фабрикой обуви имеет различные дефекты отделки. Какова вероятность того, что в партии из 200 пар, поступившей в магазин будут иметь дефекты отделки:
а) 60 пар; б) от 60 до 70 пар.
53. По данным опроса установлено, что 30% покупателей требуется женская обувь 37 размера. Известно, что ежедневно магазин в среднем посещают 189 человек. Найдите наивероятнейшее число покупателей, которым потребуется женская обувь 37 размера, и вычислите соответствующую этому числу вероятность.
54. Работниками магазина установлено, что в среднем 55% телевизоров не требуют дополнительной регулировки при продаже. Найти наивероятнейшее число телевизоров, не требующих регулировки, в партии из 110 телевизоров и вычислите соответствующую этому числу вероятность.
55. Известно, что в среднем 64% студентов потока выполняют контрольные работы в срок. Какова вероятность того, что из 100 студентов потока задержат представление контрольных работ:
а) 30 студентов; б) от 30 до 48 студентов.
56. Установлено, что третья часть покупателей желает приобрести модную одежду. Магазин посещает в среднем 800 человек в месяц. Найдите наивероятнейшее число покупателей, желающих приобрести модную одежду и вычислите соответствующую этому числу вероятность.
57. Известно, что 14% стаканов, изготавливаемых на данном предприятии имеют дефект. Какова вероятность того, что из 300 стаканов данной партии:
а) имеют дефект 45; б) не имеют дефекта от 230 до 250.
58. Установлено, что предприятие бытового обслуживания выполняет в срок в среднем 60% заказов. Какова вероятность того, что из 150 заказов будут выполнены в срок:
а) 90 заказов; б) от 90 до 107 заказов.
59. Известно, что в данном технологическом процессе 10% изделий имеют дефект. Какова вероятность того, что в партии из 400 изделий не будут иметь дефекта:
а) 342 изделия; б) от 342 до 370 изделий.
60. Известно, что 70% поставляемого в магазин товара составляют изделия первого сорта. Найдите наивероятнейшее число товаров первого сорта в партии из 400 изделий и вычислите соответствующую этому числу вероятность.