Корреляционный анализ
Корреляция – связь между двумя или несколькими исследуемыми событиями, явлениями или величинами. Так, в химической технологии достаточно продуктивно используется корреляционный анализ для установления влияния состава исходного сырья, руд, потоков на технологические и технико-экономические показатели производства (степень превращения в продукт, степень извлечения ценных компонентов из руд, качество продукта, себестоимость получения продукта и т.п.). Он позволяет также выявить влияние условий работы оборудования, технологических коллективов и факторов, изменяющихся случайным образом (содержание примесей, колебания расходов потоков, переходные режимы работы оборудования, аварийные остановки и т.п.) на основные показатели, что необходимо для оптимизации режимов производства.
Корреляционный анализ используется, когда отсутствуют теоретические зависимости, когда связь между явлениями только предполагается и носит вероятностный характер. Методами корреляционного анализа исследуют наличие случайных связей между независимыми переменными, сам факт существования или статистическую гипотезу о наличии или отсутствии связи. Результат корреляционного анализа также носит вероятностный характер, так как заключение о наличии или отсутствии связи принимается с некоторой наперед заданной доверительной вероятностью.
Корреляционный анализ заключается в определении и анализе коэффициентов корреляции, путем сравнения найденных коэффициентов корреляции с критическими значениями, указывающими на существование значимой корреляционной связи.
Качественную оценку между двумя исследуемыми величинами Х1 и Х2 можно представить графически (рис.5.3). При наличии строго определенной (детерминированной) линейной связи между величинами Х1 и Х2 график зависимости Х2=f(X1) выглядит в виде прямой линии, на которой каждому значению Х1 соответствуют величины Х2, отсутствует случайное рассеяние точек. Такой график описывается уравнением:
Х2=а+вХ1 (1)
где а - свободный коэффициент;
в - тангенс угла наклона прямой линии Х2 к оси Х1.
При наличии вероятностной линейной зависимости Х2 от Х1, носящей случайный характер, график изображается в виде совокупности точек, лежащих вблизи прямой линии (рис.5.4-5.5). Величина отклонения экспериментальных точек от прямой линии указывает на величину корреляции между величинами Х1 и Х2. Чем сильнее корреляционная связь между Х1 и Х2, тем меньше отклонения точек от прямой линии. При отсутствии корреляционной связи между Х1 и Х2 точки на графике можно представить в виде области, имеющей форму круга (рис.5.6). В этом случае между точками можно провести бесчисленное количество прямых линий.
 | |||
|
Рис.5.3. Детерминированная линейная связь между Х1 и Х2
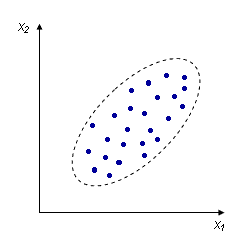
Рис.5.4. Положительная связь Х1 с Х2 Рис.5.5. Отрицательная связь Х1 с Х2
Рис.5.6. Отсутствие связи между
случайными величинами Х1 и Х2
Количественной оценкой корреляционной связи между величинами Х и У является коэффициент корреляции rxy. Он измеряет силу линейной связи между Y и X и может принимать значения от -1 до 1. При положительной величине коэффициента корреляции (положительная корреляционная связь) росту величины Х соответствует возрастание величины У. При отрицательной величине коэффициента корреляции (отрицательная корреляционная связь) росту величины Х соответствует уменьшение величины У. Если величины X и Y независимы, то коэффициент корреляции rxy =0.
Коэффициент корреляции rxy вычисляют по величине ковариации:
rxy = cov (X,Y)/SxSy (2)
где cov (X,Y)= å(Хi-X)(Yi-Y)/(n-1) - ковариация;
Sx- среднее квадратическое отклонение величин Х;
Sy- среднее квадратическое отклонение величин У.
Коэффициент корреляции является случайной величиной, поскольку вычисляется из случайных величин. Две случайные величины X и Y являются коррелированными, если их коэффициент корреляции отличен от нуля. Допустим, что выборочный коэффициент корреляции, найденный по выборке, оказался отличным от нуля. Так как выборка отобрана случайно, то отсюда еще нельзя заключить, что коэффициент корреляции генеральной совокупности также отличен от нуля. Возникает необходимость проверить гипотезу о значимости (существенности) выборочного коэффициента корреляции (или о равенстве нулю коэффициента корреляции генеральной совокупности). Если гипотеза о равенстве нулю генерального коэффициента корреляции будет отвергнута, то выборочный коэффициент корреляции значим, а величины X и Y коррелированны; если гипотеза принята, то выборочный коэффициент корреляции незначим, а величины X и Y некоррелированы.
Для того чтобы при заданном уровне значимости проверить гипотезу о равенстве нулю генерального коэффициента корреляции нормально распределенной случайной величины необходимо вычислить наблюдаемое значение критерия tнабл:
(3)
где rxy - значение коэффициента корреляции, вычисленное по формуле (2).
По таблице критических точек распределения Стьюдента, по заданному уровню значимости и числу степеней свободы f =n-2 найти критическую точку tкр(;f) для двусторонней критической области. Затем производится сравнение абсолютной величины |tнабл| и tкр. Если |tнабл|<tкр –коэффициент корреляции незначим, а если |tнабл|>tкр - выборочный коэффициент корреляции значимо отличается от нуля и случайные величины коррелированны.
Значимость коэффициента корреляции также можно определить /21/ по формуле:
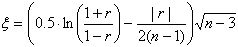(4)
Вычисленную величину ξ сравнивают с табличным значением коэффициента Стьюдента t(Р=0.95;f= 
)=1.96. Если тестовая статистика ξ больше табличного значения коэффициента Стьюдента t, то коэффициент корреляции значимо отличается от нуля.
Значимость отличия между двумя коэффициентами корреляции определяют по тестовой статистике /21/:
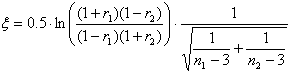(5)
Вычисленную величину ξ сравнивают с табличным значением коэффициента Стьюдента t(Р=0.95;f= )=1.96. Если статистика ξ больше табличного значения коэффициента Стьюдента t, то коэффициенты корреляции значимо отличается.
Пример корреляционного анализа
При получении 98%-го хлорида калия, важно знать между какими компонентами существует корреляционная связь, с какими примесями в сильвинитовой руде ассоциируется бромид-ион. В связи с этим проводят корреляционный анализ и выявляют корреляционные связи содержания компонентов в составе сильвинитовой руды. Состав сильвинитовой руды Березниковского калийного рудоуправления №1 приведен в табл.5.9.
Таблица 5.9
Состав компонентов сильвинитовой руды ствола №3, БКРУ-1
(данные за 2006 г.)
| № | Месяц | н.о. | KCl | NaCl | MgCl2 | CaSO4 | Br- |
| январь | 1,9 | 27,6 | 0,17 | 2,1 | 0,062 | ||
| 1,7 | 27,3 | 68,5 | 0,18 | 2,11 | 0,062 | ||
| 27,2 | 68,3 | 0,23 | 2,20 | 0,064 | |||
| февраль | 1,8 | 67,8 | 0,14 | 1,94 | 0,064 | ||
| 1,8 | 27,7 | 68,1 | 0,15 | 1,99 | 0,065 | ||
| 1,5 | 26,2 | 69,9 | 0,13 | 1,98 | 0,062 | ||
| март | 1,7 | 27,5 | 68,7 | 0,16 | 1,83 | 0,066 | |
| 1,7 | 68,8 | 0,15 | 2,07 | 0,061 | |||
| 1,8 | 27,7 | 68,3 | 0,09 | 1,96 | 0,063 | ||
| апрель | 1,6 | 27,9 | 68,3 | 0,12 | 1,78 | 0,064 | |
| 1,4 | 68,7 | 0,11 | 1,78 | 0,067 | |||
| 1,7 | 67,9 | 0,11 | 1,96 | 0,064 | |||
| май | 1,5 | 27,5 | 68,7 | 0,23 | 1,89 | 0,065 | |
| 1,9 | 27,3 | 68,2 | 0,18 | 1,95 | 0,061 | ||
| 1,7 | 27,3 | 68,8 | 0,15 | 1,83 | 0,063 | ||
| июнь | 1,9 | 28,3 | 67,5 | 0,14 | 1,96 | 0,063 | |
| 1,8 | 27,5 | 68,7 | 0,14 | 1,91 | 0,064 | ||
| 1,8 | 27,5 | 68,5 | 0,18 | 1,94 | 0,063 | ||
| июль | 1,8 | 26,7 | 69,4 | 0,13 | 1,89 | 0,063 | |
| 1,7 | 27,7 | 68,3 | 0,13 | 1,94 | 0,061 | ||
| 1,7 | 27,2 | 68,6 | 0,16 | 2,02 | 0,062 | ||
| август | 1,8 | 27,2 | 68,8 | 0,14 | 1,86 | 0,065 | |
| 1,8 | 28,4 | 67,2 | 0,11 | 2,18 | 0,062 | ||
| 1,9 | 67,6 | 0,17 | 2,01 | 0,063 | |||
| сентябрь | 1,8 | 27,5 | 68,3 | 0,19 | 1,92 | 0,063 | |
| 1,7 | 27,2 | 68,8 | 0,14 | 1,85 | 0,064 | ||
| 1,9 | 27,5 | 0,21 | 2,00 | 0,064 | |||
| октябрь | 1,9 | 27,4 | 68,5 | 0,15 | 1,94 | 0,063 | |
| 1,7 | 27,4 | 68,5 | 0,17 | 2,01 | 0,063 | ||
| 1,7 | 27,5 | 68,6 | 0,11 | 1,98 | 0,063 | ||
| ноябрь | 1,7 | 27,7 | 68,3 | 0,13 | 1,99 | 0,064 | |
| 1,7 | 27,6 | 68,4 | 0,14 | 1,90 | 0,063 | ||
| 1,9 | 68,8 | 0,13 | 2,07 | 0,061 |
Примечание: но – нерастворимый в воде остаток.
Для проведения корреляционного анализа используем прикладной пакет «Анализ данных» программы Microsoft Excel. Для этого копируем данные табл.1 в программу Microsoft Excel, сохраняя в памяти компьютера файл под определенным именем. Далее, в меню программы Microsoft Excel выберем кнопку “Сервис”, после нажатия на которую выберем кнопку “Анализ данных”.
Если пакет “Анализ данных” не установлен в программе Microsoft Excel, то для его установки выполняют указанные в разделе Статистический анализ операции.
В пакете “Анализ данных” выбирают инструмент “Корреляция” и нажимают “ОК”. В программе появляется окно запроса входного интервала анализируемых данных. С помощью мышки выделяют входной интервал анализируемых данных (имя и содержание столбцов, начиная с первого столбца “н.о.”). В меню “Корреляция” указывают группирование – (по столбцам или по строкам), выбирают – “По столбцам”. Для идентификации столбцов в выводимой таблице ставим метку в строке “Метки в первой строке”. В параметрах вывода данных ставят метку напротив строки – “Новый рабочий лист”. При этом, данные расчетов коэффициентов корреляции выведутся на новый рабочий лист программы Microsoft Excel в виде табл.5.10.
Таблица 5.10
Значения коэффициентов корреляции компонентов
сильвинитовой руды БКРУ-1
| н.о. | KCl | NaCl | MgCl2 | CaSO4 | Br- | |
| Н.о. | ||||||
| KCl | 0,093357 | |||||
| NaCl | -0,4618 | -0,87199 | ||||
| MgCl2 | 0,273002 | -0,19928 | -0,04059 | |||
| CaSO4 | 0,495106 | -0,03191 | -0,33646 | 0,25169 | ||
| Br- | -0,32867 | 0,282824 | 0,019446 | 0,029904 | -0,53145 |
Для оценки значимости вычисленных коэффициентов корреляции используем выражение:
Для приведенного примера n=33. Вычисленные по этой формуле величины tнабл приведены в табл.5.11.
Таблица 5.11
Значения коэффициентов tнабл
| н.о. | KCl | NaCl | MgCl2 | CaSO4 | Br- | |
| Н.о. | ||||||
| KCl | 0,52207 | |||||
| NaCl | -2,8988 | -9,91788 | ||||
| MgCl2 | 1,580031 | -1,13225 | -0,22618 | |||
| CaSO4 | 3,172802 | -0,17776 | -1,98931 | 1,447964 | ||
| Br- | -1,9376 | 1,641726 | 0,108291 | 0,166573 | -3,4931 |
Величину tкр находят по статистической таблице или по функции: =СТЬЮДРАСПОБР(0,05;32), принимая уровень значимости a=0.05, число степеней свободы f=n-1= 32. Отсюда, найдено критическое значение tкр=2,036933.
Сравнение |tнабл | и tкр показало, что к значимым коэффициентам регрессии относятся только четыре выделенных в табл. 2 коэффициента корреляции.
Из анализа данных табл.5.11 следует, что значимая корреляционная связь существует между: 1) содержанием нерастворимого остатка и содержанием NaC1 и СаSO4; 2) содержанием КС1 и NaC1; 3) содержанием СаSO4 и бромид-ионом. По знаку коэффициентов корреляции можно заключить, что чем меньше содержание в сильвинитовой руде хлорида натрия и выше содержание сульфата кальция, тем больше содержание в руде нерастворимого остатка. Содержание основного вещества КС1 в руде возрастает при снижении содержания примеси хлорида натрия. Содержание примеси бромид-иона снижается при увеличении в руде примеси сульфата кальция. По величине коэффициента корреляции можно заключить, что наибольшая корреляционная связь существует между основными компонентами сильвинитовой руды – хлоридами КС1 и NaC1 (r=-0.872).
Найденные зависимости полезны для оптимизации работы флотационных и галургических производств, перерабатывающих сильвинитовые руды.