IIIтип. Решение задач на доказательство с применением осевой симметрии.

I тип. Задачи на построение образов фигур при движении.

№1. Дан произвольный четырёхугольник АBCD, у которого диагональ АС является биссектрисой угла BAD. Построить образ данного четырёхугольника при движении 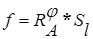, где ℓ = (AC), φ = .

№2 ABCD – трапеция, диагонали конторой пересекаются в точке О. Построить образ данной трапеции при движении .

№3 В треугольнике ∆ABC [AD] –, биссектриса . Построить образ ∆ABC при движении , где ℓ = (AD), φ = .

№4Построить образ параллелограмма ABCD в композиции , где φ = , а О – центр параллелограмма.

№5Дан разносторонний ∆АВС с биссектрисой AD. Построить образ ∆АВС в движении , где , ℓ – прямая, проходящая через середину[АС].

№6Построить образ параллелограмма ABCD в композиции 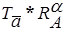, где α = DAB, , где О – центр параллелограмма.

№7Построить образ ромба ABCD в композиции , где О –центр ромба, φ = 90⁰, , [ОМ) – биссектриса DOC.

№8АВСD – квадрат. Построить его образ в композиции , где ℓ = (DA), , О – центр квадрата, А₁ – середина [ВС].

№9Построить образ произвольной трапеции ABCD в композиции , если α = DOC, О = (АС) (DB).

№10Построить образ ∆АВС в композиции , если ∆АВС равносторонний, точка М – его центр, , .

II тип. Задачи на выделение элементов, определяющих преобразование.

№11 Даны две окружности равных радиусов ω₁(О₁,R) и ω₂(О₂,R) и произвольный ∆АВС. Построить образ ∆АВС в движении, которое меняет ориентацию фигуры не имеет неподвижных точек, и при котором ω₁(О₁)→ ω₂(О₂) и (О₁О₂)→(О₁О₂).

№12 Даны два равных не параллельных отрезка [AB] и [A₁B₁] и ∆ MNP. Построить образ ∆MNP в скользящей симметрии, при которой [AB] → [A₁B₁]

№13 Дан ∆АВС, построить его образ при повороте, который А → В, а прямую (СА) → (СВ).

№14 Даны две окружности равных радиусов ω₁(О₁,R) и ω₂(О₂,R) и произвольный ∆АВС. Построить образ ∆АВС в движении, которое меняет ориентацию фигуры не имеет неподвижных точек, и при котором ω₁(О₁)→ ω₂(О₂) и (О₁О₂)→(О₁О₂).

№15 В ∆АВС точки А₁, В₁, С₁ – середины его сторон ВС, АС, АВ. Построить образ ∆АВС в движении, которое не имеет неподвижных точек, меняет ориентацию фигуры и при котором (В₁С₁)→ (В₁С₁) и В→А₁.

№16 В произвольном треугольнике ∆АВС проведены медиана ВВ₁ и биссектриса АА₀. Построить образ ∆АВС в движении, которое не меняет ориентацию фигуры, имеет одну неподвижную точку, в которой (АА₀)→(АА₀) и (ВВ₁)→(ВВ₁).

№17 Дан разносторонний ∆АВС. Построить его образ в движении, которое имеет одну неподвижную точку, не меняет ориентацию фигур и при котором А→В, а прямая СА→СВ.

№18 Две окружности, равных радиусов ω₁(О₁,R) и ω₂(О₂,R) касаются в точке В. Точка А₁ = ω₁(О₁) (О₁О₂). Точка А₂ ω₂(О₂) и [А₂О₂] (О₁О₂). Построить образ точки В в движении, которое не меняет ориентации фигуры, имеет одну неподвижную точку, при котором О₁→О₂ и А₁→А₂.

№19 Точки M и L – середины сторон АВ и АС ∆АВС в движении, которое не меняет ориентации фигуры, не имеет неподвижных точек, при котором (АВ)→(АВ) и (ВС)→(ML).

№20Даны два конгруэнтных произвольно расположенных квадрата. Построить центр поворота, отображающего один квадрат на другой

IIIтип. Решение задач на доказательство с применением осевой симметрии.

№21. На основаниях равнобочной трапеции вне её построены квадраты. Доказать, что отрезок, соединяющий центры квадратов проходит через точку пересечения диагоналей трапеции.

№22. В равнобедренном треугольнике АВС боковые стороны ВА и ВС соответственно разделены точками М и Р в отношении 1:3, считая от точки В. Доказать, что прямые АР и МС пересекаются в точке, лежащей на высоте треугольника.

№23. Две окружности ω(О₁, R₁) и ω(О₂, R₂) пересекаются в точках P и Q. Доказать, что угол между касательными в точке Р, равен углу между касательными, проведёнными в в точке Q.

№24. На равных сторонах АВ и ВС треугольника АВС вне его построены квадраты с центрами О₁ и О₂. Доказать, что прямые О₁А и О₂С пересекаются на биссектрисе угла В треугольника и отрезки О₁А и О₂С равны.

№25. Точки А и В расположены на различных сторонах угла на одинаковых расстояниях от его вершины О и соединены с произвольной точкой Q биссектрисы угла.

№26. Доказать, что [AQ] = [BQ] и что [AQ] и [BQ] образуют с прямой OQ равные углы. Стороны AB, BC, СА правильного треугольника АВС разделены точками С₁, А₁, В₁ (соответственно) в отношении│АС₁│:│С₁В│= =│СВ₁│:│В₁А│ = │ВА₁│:│ А₁С│= 2:1. Доказать, что треугольник А₁В₁С₁ – правильный.

№27. Точки А и В расположены на различных сторонах угла на одинаковых расстояниях от его вершины О и соединены с произвольной точкой Q биссектрисы угла. Доказать, что [AQ] = [BQ] и что [AQ] и [BQ] образуют с прямой OQ равные углы.

№28. Точки А и В расположены на различных сторонах угла на одинаковых расстояниях от его вершины О и соединены с произвольной точкой Q биссектрисы угла. Доказать, что [AQ] = [BQ] и что [AQ] и [BQ] образуют с прямой OQ равные углы.

№29. Точки А и В расположены на различных сторонах угла на одинаковых расстояниях от его вершины О и соединены с произвольной точкой Q биссектрисы угла. Доказать, что [AQ] = [BQ] и что [AQ] и [BQ] образуют с прямой OQ равные углы.

№30. Даны угол и окружность, центр которой лежит на биссектрисе этого угла и которая пересекает стороны угла. Доказать, что хорды окружности, расположенные на сторонах угла равны между собой.