Теорема 1. Формула Грина.

Пусть в области , граница которого - замкнутый контур 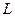, являющийся односвязным множеством, задано плоское векторное поле .

Тогда верна такая формула: .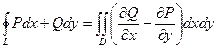

То есть, работа силы по границе области равна двойному интегралу от величины 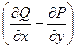по этой плоской области.

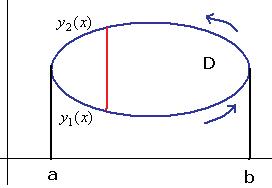
Доказательство (ДОК 1). Спроецируем область на ось Ох, обозначим границы проекции: точки . Сама граница области тогда условно подразделяется на две линии, снизу , а сверху . Чтобы движение по замкнутому контуру происходило против часовой стрелки, надо по двигаться слева направо, а по справа налево.

 

Рассмотрим подробнее интеграл от функции по границе области. В соответствии со всем сказанным, он может быть записан так: . Но во втором интеграле можно изменить на , сменив знак.

и их можно объединить

=

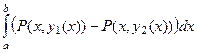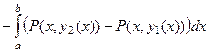
разность, которая внутри интеграла, является результатом применения формулы Ньютона-Лейбница по переменной :

запишем это в виде: .

Но если формула Ньютона-Лейбница применяется к , значит, это первообразная по , а она очевидно, является первообразной от своей производной 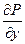. То есть:

= а этой как раз и есть двойной интеграл по области D.

= .

Аналогично можно спроецировать область D на ось Оу, допустим проекция займёт некоторый отрезок . Левую и правую линии, составляющие замкнутый контур, обозначим 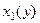и . Правая здесь будет (она дальше от оси Оу).

Тогда = = =

= = .

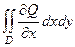Сложим два полученных равенства и получается двойной интеграл

.

 

Пример. Решим тот же самый пример, что рассматривали недавно, работа поля при движении точки по единичной окружности, но сделаем это теперь по формуле Грина.

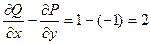. Тогда = = где D - круг радиуса 1. Тогда интеграл от 1 это его площадь. = = .

 

Потенциальные поля

 

Скалярное поле, или скалярная функция: .

Векторная функция, которая отображает называется векторным полем.

Заметим, что градиент скалярной функции - это векторная функция:

, ,

То есть, по скалярному полю всегда можно построить некоторое векторное.

Пример: . Тогда .

 

Обратная задача: если даны некоторые 3 скалярные функции, т.е. векторное поле, всегда ли они являются частными производными какой-то единой скалярной функции? Оказывается, нет.

Определение. Если существует такая скалярная функция , что выполняется , , , (то есть их общая первообразная), то векторное поле называется потенциальным, а функция называется потенциалом поля .

 

Кстати, если - потенциал, то - тоже потенциал, ведь , , .

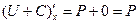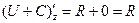Потенциал определяется с точностью до константы (точно так же как и первообразная). Именно поэтому в физике важна именно разность потенциалов, а не сам потенциал.

 

Примеры.

Пример не потенциального поля.

. Первообразная от 1 компоненты по это , однако первообразная по от второй компоненты совсем другая:

, они не совпадают.

Пример потенциального поля.

. Его потенциал: .

 

Далее нам надо научиться выяснять 2 вопроса:

1) выяснять, является ли поле потенциальным.

2) вычислять потенциал, если оно потенциально.

Теорема 2. Криволинейный интеграл 2 рода не зависит от пути циркуляция по замкнутому контуру равна 0.

Доказательство (ДОК 2).

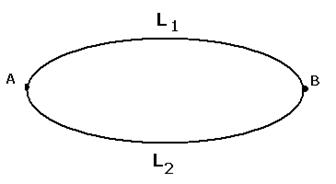
Необходимость. Пусть интеграл зависит только от начальной и конечной точки, и не зависит от пути, соединяющего точки А,В. Возьмём какой-нибудь замкнутый контур, разобьём его какими-нибудь случайно взятыми точками. Докажем, что циркуляция равна 0.

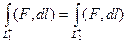
. Но так как объединение 2 частей в замкнутый контур это 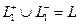, то получается: .

Достаточность.

Пусть для любого замкнутого контура 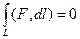. Если даны какие-то точки А,В, и какие-то две различные линии, соединяющие их, то эти две линии можно объединить в единый замкнутый контур.

 

,

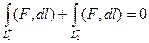
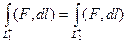что и требовалось доказать.

 

Теорема 3. Поле F потенциально криволинейный интеграл 2 рода от F не зависит от пути, причём тогда потенциал в любой точке вычисляется в виде где A₀ - некоторая начальная точка, как правило (0,0,0).

Доказательство (ДОК 3).

Необходимость. Если поле потенциально то , ,

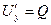а тогда в интеграле получится 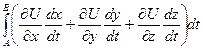а по формуле полного дифференциала это 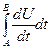но ведь первообразная от производной - это сама функция U, тогда работа поля в итоге равна = то есть зависит только от начальной и конечной точки.

Достаточность.

Если криволинейный интеграл для поля (P,Q,R) не зависит от пути, возьмём начальную точку, например начало координат (0,0,0). Введём некоторую скалярную функцию U(x,y,z) равную работе поля от (0,0,0) до точки А(x,y,z). То есть .

А теперь мы докажем, что именно эта функция является потенциалом.

Составим путь из дуги от 0 до А и дополнительного маленького горизонтального отрезка вдоль оси Ох. Интеграл от 0 до А равен U(А). Интеграл от 0 до А₁ равен U(А₁).

Координаты точек: А (x,y,z) и А₁ (x+∆x,y,z).

Тогда = но в интеграле по отрезку АА₁ меняется только x, при этом y, z константы, то есть dy = 0, dz = 0.

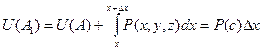для некоторой промежуточной точки с, где достигается среднее значение.

Тогда , следовательно, = .

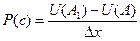Но точка с тоже стремится к х при ∆x →0.

То есть . Итак, .

Аналогично, рассматривая точку А₁ с координатами А₁ (x,y+∆y,z) получили бы , а если то А₁ (x,y,z+∆z) то . Итак, поле потенциально и U(x,y,z), равная работе силы по перемещению от начальной точки до (x,y,z), является потенциалом.

 

Следствие. Поле F потенциально 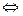циркуляция по замкнутому контуру равна 0.

 

Доказанный критерий позволяет вычислить потенциал, если известно, что поле потенциально, однако практически ничем не поможет выяснить изначально вопрос о том, потенциально ли поле. Ведь кривых, соединяющих две точки А,В бесконечно много, и невозможно вычислить интегралы по всем этим кривым. Поэтому для проверки потенциальности необходим другой критерий.

ЛЕКЦИЯ 2. 09.09.2019

Теорема 4. 1) Если поле потенциально то симметрична производная матрица .

2) Если граница области D, в которой задано векторное поле, является односвязным множеством, и симметрична производная матрица , то поле потенциально.

Доказательство (ДОК 4).

1) Необходимость. Пусть поле потенциально. Тогда являются производными от какой-то общей функции , т.е. 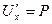, 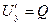. тогда , . Но смешанные частные производные 2-го порядка совпадают, значит, = .

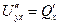а следовательно, = .

2) Достаточность. Здесь мы будем использовать формулу Грина, которую доказали ранее, а там фактически неявно это и предполагали при записи двойного интеграла, когда для рассматривался отрезок , то есть такая ситуация, как для кольца, не рассматривается, а только множества без внутренних пустот.

Если производная матрица симметрична, то (в других обозначениях 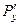= ). Тогда , и двойной интеграл по любой плоской области равен 0: .

Но ведь тогда для любого замкнутого контура получается, что по формуле Грина, если двойной интеграл по его внутренней области 0, то и циркуляция по границе тоже 0:

= 0,

а если для любого контура циркуляция 0, то поле потенциально, что следует из теорем 1 и 2, доказанных ранее.

В 3-мерном случае требуется совпадение трёх пар производных, доказательство показано пока для 2-мерного случая, чтобы использовать формулу Грина.

 

Алгоритм нахождения потенциала.

1. Выяснить потенциальность поля, проверив симметричность производной матрицы (она сотоит из всех частных производных: от всех компонент векторного поля по всем переменным).

2. Найти потенциал, как скалярную функцию, равную криволинейному интегралу от фиксированной точки до произвольной.

Как правило, в качестве «начальной» фиксированной точки рассматривают начало координат, если же в функциях присутствуют к примеру или , то можно взять в качестве начальной точку (1,1) а не (0,0).

Путь от начальной точки до может быть по любой кривой, но практически лучше по ломаной, состоящей из отрезков, параллельных осям координат. Сначала от (0,0) к (x,0) а затем 2-е звено до точки (x,y).

Пример. Доказать, что поле потенциально и найти потенциал.

Решение. Шаг 1. Сначала найдём производную матрицу, вычислив все частные производные по всем переменным:

= . Мы видим, что она симметрична. Значит, поле потенциально.

Шаг 2. Найдём криволинейный интеграл от (0,0) до 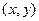, соединив с помощью ломаной. Лучше всего даже обозначить конечную точку 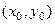, чтобы не путать обозначение переменной, по которой ведётся интегрирование, и верхнего предела. Вычислив 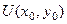, затем мы учтём тот факт, что эта точка была произвольной, и сможем записать уже просто .

разбивается на сумму двух интегралов, по каждому участку ломаной, причём на каждом из них обнуляется один из двух дифференциалов: на горизонтальном отрезке меняется только , а тогда , на вертикальном меняется , тогда .

=

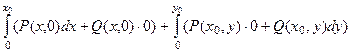
в обоих интегралах формально присутствуют оба слагаемых, но одно из них обнуляется, поэтому выглядит далее так, как будто распределилось по одному слагаемому в каждый интеграл.

в первом фиксировано , а на втором участке переменная уже достигла и далее не меняется, поэтому там .

Для данного конкретного примера получается

= = = .

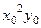Итак, , тогда можно сказать, что .

Проверка. , .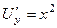